Chapter 17. Trees and Graphs

In This Chapter

In this chapter we will discuss tree data structures, like trees and graphs. The abilities of these data structures are really important for the modern programming. Each of this data structures is used for building a model of real life problems, which are efficiently solved using this model. We will explain what tree data structures are and will review their main advantages and disadvantages. We will present example implementations and problems showing their practical usage. We will focus on binary trees, binary search trees and self-balancing binary search tree. We will explain what graph is, the types of graphs, how to represent a graph in the memory (graph implementation) and where graphs are used in our life and in the computer technologies. We will see where in .NET Framework self-balancing binary search trees are implemented and how to use them.

Content

• Video
• Presentation
• Mind Maps
• In This Chapter
• Tree Data Structures
• ­Trees
• Graphs
• Exercises
• Solutions and Guidelines
• Demonstrations (source code)
• Discussion Forum

Video

Presentation

Mind Maps

Tree Data Structures

Very often we have to describe a group of real life objects, which have such relation to one another that we cannot use linear data structures for their description. In this chapter, we will give examples of such branched structures. We will explain their properties and the real life problems, which inspired their creation and further development.

A tree-like data structure or branched data structure consists of set of elements (nodes) which could be linked to other elements, sometimes hierarchically, sometimes not. Trees represent hierarchies, while graphs represent more general relations such as the map of city.

­Trees

Trees are very often used in programming, because they naturally represent all kind of object hierarchies from our surroundings. Let’s give an example, before we explain the trees’ terminology.

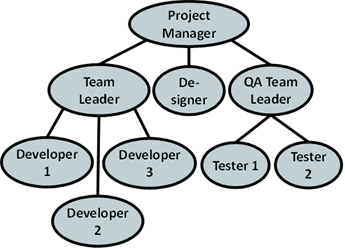
Example – Hierarchy of the Participants in a Project

We have a team, responsible for the development of certain software project.

The participants in it have manager-subordinates relations. Our team consists of 9 teammates:

What is the information we can get from this hierarchy? The direct boss of the developers is the "Team Leader", but indirectly they are subordinate to the "Project Manager". The "Team Leader" is subordinate only to the "Project Manager". On the other hand "Developer 1" has no subordinates. The "Project Manager" is the highest in the hierarchy and has no manager.

The same way we can describe every participant in the project. We see that such a little figure gives us so much information.

Trees Terminology

For a better understanding of this part of the chapter we recommend to the reader at every step to draw an analogy between the abstract meaning and its practical usage in everyday life.

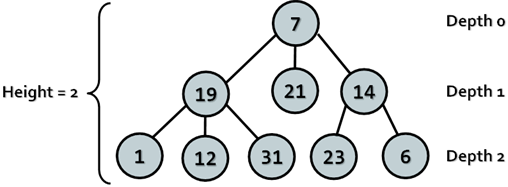
We will simplify the figure describing our hierarchy. We assume that it consists of circles and lines connecting them. For convenience we name the circles with unique numbers, so that we can easily specify about which one we are talking about.

We will call every circle a node and each line an edge. Nodes "19", "21", "14" are below node "7" and are directly connected to it. This nodes we are called direct descendants (child nodes) of node "7", and node "7" their parent. The same way "1", "12" and "31" are children of "19" and "19" is their parent. Intuitively we can say that "21" is sibling of "19", because they are both children of "7" (the reverse is also true – "19" is sibling of "21").For "1", "12", "31", "23" and "6" node "7" precedes them in the hierarchy, so he is their indirect parent – ancestor, ant they are called his descendants.

Root is called the node without parent. In our example this is node "7"

Leaf is a node without child nodes. In our example – "1", "12", "31", "21", "23" and "6".

Internal nodes are the nodes, which are not leaf or root (all nodes, which have parent and at least one child). Such nodes are "19" and "14".

Path is called a sequence of nodes connected with edges, in which there is no repetition of nodes. Example of path is the sequence "1", "19", "7" and "21". The sequence "1", "19" and "23" is not a path, because "19" and "23" are not connected.

Path length is the number of edges, connecting the sequence of nodes in the path. Actually it is equal to the number of nodes in the path minus 1. The length of our example for path ("1", "19", "7" and "21") is three.

Depth of a node we will call the length of the path from the root to certain node. In our example "7" as root has depth zero, "19" has depth one and "23" – depth two.

Here is the definition about tree:

Tree – a recursive data structure, which consists of nodes, connected with edges. The following statements are true for trees:

-     Each node can have 0 or more direct descendants (children).

-     Each node has at most one parent. There is only one special node without parent – the root (if the tree is not empty).

-     All nodes are reachable from the root – there is a path from the root to each node in the tree.

We can give more simple definition of tree: a node is a tree and this node can have zero or more children, which are also trees.

Height of tree – is the maximum depth of all its nodes. In our example the tree height is 2.

Degree of node we call the number of direct children of the given node. The degree of "19" and "7" is three, but the degree of "14" is two. The leaves have degree zero.

Branching factor is the maximum of the degrees of all nodes in the tree. In our example the maximum degree of the nodes is 3, so the branching factor is 3.

Tree Implementation – Example

Now we will see how to represent trees as data structure in programming. We will implement a tree dynamically. Our tree will contain numbers inside its nodes, and each node will have a list of zero or more children, which are trees too (following our recursive definition).

Each node is recursively defined using itself. Each node of the tree (TreeNode<T>) contains a list of children, which are nodes (TreeNode<T>). The tree itself is another class Tree<T> which can be empty or can have a root node. Tree<T> implements basic operations over trees like construction and traversal.

Let’s have a look at the source code of our dynamic tree representation:

using System; using System.Collections.Generic;   /// <summary>Represents a tree node</summary> /// <typeparam name="T">the type of the values in nodes /// </typeparam> public class TreeNode<T> {     // Contains the value of the node     private T value;       // Shows whether the current node has a parent or not     private bool hasParent;       // Contains the children of the node (zero or more)     private List<TreeNode<T>> children;       /// <summary>Constructs a tree node</summary>     /// <param name="value">the value of the node</param>     public TreeNode(T value)     {         if (value == null)         {             throw new ArgumentNullException(                 "Cannot insert null value!");         }         this.value = value;         this.children = new List<TreeNode<T>>();     }       /// <summary>The value of the node</summary>     public T Value     {         get         {             return this.value;         }         set         {             this.value = value;         }     }       /// <summary>The number of node's children</summary>     public int ChildrenCount     {         get         {             return this.children.Count;         }     }       /// <summary>Adds child to the node</summary>     /// <param name="child">the child to be added</param>     public void AddChild(TreeNode<T> child)     {         if (child == null)         {             throw new ArgumentNullException(                 "Cannot insert null value!");         }           if (child.hasParent)         {             throw new ArgumentException(                 "The node already has a parent!");         }           child.hasParent = true;         this.children.Add(child);     }       /// <summary>     /// Gets the child of the node at given index     /// </summary>     /// <param name="index">the index of the desired child</param>     /// <returns>the child on the given position</returns>     public TreeNode<T> GetChild(int index)     {         return this.children[index];     } }   /// <summary>Represents a tree data structure</summary> /// <typeparam name="T">the type of the values in the /// tree</typeparam> public class Tree<T> {     // The root of the tree     private TreeNode<T> root;       /// <summary>Constructs the tree</summary>     /// <param name="value">the value of the node</param>     public Tree(T value)     {         if (value == null)         {             throw new ArgumentNullException(                 "Cannot insert null value!");         }           this.root = new TreeNode<T>(value);     }       /// <summary>Constructs the tree</summary>     /// <param name="value">the value of the root node</param>     /// <param name="children">the children of the root     /// node</param>     public Tree(T value, params Tree<T>[] children)         : this(value)     {         foreach (Tree<T> child in children)         {             this.root.AddChild(child.root);         }     }       /// <summary>     /// The root node or null if the tree is empty     /// </summary>     public TreeNode<T> Root     {         get         {             return this.root;         }     }       /// <summary>Traverses and prints tree in     /// Depth-First Search (DFS) manner</summary>     /// <param name="root">the root of the tree to be     /// traversed</param>     /// <param name="spaces">the spaces used for     /// representation of the parent-child relation</param>     private void PrintDFS(TreeNode<T> root, string spaces)     {         if (this.root == null)         {             return;         }           Console.WriteLine(spaces + root.Value);           TreeNode<T> child = null;         for (int i = 0; i < root.ChildrenCount; i++)         {             child = root.GetChild(i);             PrintDFS(child, spaces + "   ");         }     }       /// <summary>Traverses and prints the tree in     /// Depth-First Search (DFS) manner</summary>     public void TraverseDFS()     {         this.PrintDFS(this.root, string.Empty);     } }   /// <summary> /// Shows a sample usage of the Tree<T> class /// </summary> public static class TreeExample {     static void Main()     {         // Create the tree from the sample         Tree<int> tree =             new Tree<int>(7,                 new Tree<int>(19,                     new Tree<int>(1),                     new Tree<int>(12),                     new Tree<int>(31)),                 new Tree<int>(21),                 new Tree<int>(14,                     new Tree<int>(23),                     new Tree<int>(6))             );           // Traverse and print the tree using Depth-First-Search         tree.TraverseDFS();           // Console output:         // 7         //       19         //        1         //        12         //        31         //       21         //       14         //        23         //        6     } }

How Does Our Implementation Work?

Let’s discuss the given code a little. In our example we have a class Tree<T>, which implements the actual tree. We also have a class TreeNode<T>, which represents a single node of the tree.

The functions associated with node, like creating a node, adding a child node to this node, and getting the number of children, are implemented at the level of TreeNode<T>.

The rest of the functionality (traversing the tree for example) is implemented at the level of Tree<T>. Logically dividing the functionality between the two classes makes our implementation more flexible.

The reason we divide the implementation in two classes is that some operations are typical for each separate node (adding a child for example), while others are about the whole tree (searching a node by its number). In this variant of the implementation, the tree is a class that knows its root and each node knows its children. In this implementation we can have an empty tree (when root = null).

Here are some details about the TreeNode<T> implementation. Each node of the tree consists of private field value and a list of children – children. The list of children consists of elements of the same type. That way each node contains a list of references to its direct children. There are also public properties for accessing the values of the fields of the node. The methods that can be called from code outside the class are:

-     AddChild(TreeNode<T> child) – adds a child

-     TreeNode<T> GetChild(int index) – returns a child by given index

-     ChildrenCount – returns the number of children of certain node

To satisfy the condition that every node has only one parent we have defined private field hasParent, which determines whether this node has parent or not. This information is used only inside the class and we need it in the AddChild(Tree<T> child) method. Inside this method we check whether the node to be added already has parent and if so we throw and exception, saying that this is impossible.

In the class Tree<T> we have only one get property TreeNode<T> Root, which returns the root of the tree.

Depth-First-Search (DFS) Traversal

In the class Tree<T> is implemented the method TraverseDFS(), that calls the private method PrintDFS(TreeNode<T> root, string spaces), which traverses the tree in depth and prints on the standard output its elements in tree layout using right displacement (adding spaces).

The Depth-First-Search algorithm aims to visit each of the tree nodes exactly one. Such a visit of all nodes is called tree traversal. There are multiple algorithms to traverse a tree but in this chapter we will discuss only two of them: DFS (depth-first search) and BFS (breadth-first search).

The DFS algorithm starts from a given node and goes as deep in the tree hierarchy as it can. When it reaches a node, which has no children to visit or all have been visited, it returns to the previous node. We can describe the depth-first search algorithm by the following simple steps:

1.  Traverse the current node (e.g. print it on the console or process it in some way).

2.  Sequentially traverse recursively each of the current nodes’ child nodes (traverse the sub-trees of the current node). This can be done by a recursive call to the same method for each child node.

Creating a Tree

We to make creating a tree easier we defined a special constructor, which takes for input parameters a node value and a list of its sub-trees. That allows us to give any number of arguments of type Tree<T> (sub-trees). We used exactly the same constructor for creating the example tree.

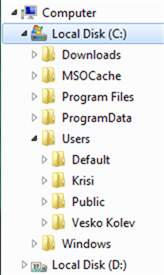
Traverse the Hard Drive Directories

Let’s start with another example of tree: the file system. Have you noticed that the directories on your hard drive are actually a hierarchical structure, which is a tree? We have folders (tree nodes) which may have child folders and files (which both are also tree nodes).

You can think of many real life examples, where trees are used, right?

Let’s get a more detailed view of Windows file system. As we know from our everyday experience, we create folders on the hard drive, which can contain subfolders and files. Subfolders can also contain subfolders and so on until you reach certain max depth limit.

The directory tree of the file system is accessible through the build in .NET functionality: the class System.IO.DirectoryInfo. It is not present as a data structure, but we can get the subfolders and files of every directory, so we can traverse the file system tree by using a standard tree traversal algorithm, such as Depth-First Search (DFS).

Below we can see what the typical directory tree in Windows looks like:

Recursive DFS Traversal of the Directories

The next example illustrates how we can recursively traverse recursively the tree structure of given folder (using Depth-First-Search) and print on the standard output its content:

DirectoryTraverserDFS.cs

using System; using System.IO;   /// <summary> /// Sample class, which traverses recursively given directory /// based on the Depth-First-Search (DFS) algorithm /// </summary> public static class DirectoryTraverserDFS {     /// <summary>     /// Traverses and prints given directory recursively     /// </summary>     /// <param name="dir">the directory to be traversed</param>     /// <param name="spaces">the spaces used for representation     /// of the parent-child relation</param>     private static void TraverseDir(DirectoryInfo dir,         string spaces)     {         // Visit the current directory         Console.WriteLine(spaces + dir.FullName);           DirectoryInfo[] children = dir.GetDirectories();           // For each child go and visit its sub-tree         foreach (DirectoryInfo child in children)         {             TraverseDir(child, spaces + "  ");         }     }       /// <summary>     /// Traverses and prints given directory recursively     /// </summary>     /// <param name="directoryPath">the path to the directory     /// which should be traversed</param>     static void TraverseDir(string directoryPath)     {         TraverseDir(new DirectoryInfo(directoryPath),             string.Empty);     }       static void Main()     {         TraverseDir("C:\\");     } }

As we can see the recursive traversal algorithm of the content of the directory is the same as the one we used for our tree.

Here we can see part of the result of the traversal:

C:\   C:\Config.Msi   C:\Documents and Settings     C:\Documents and Settings\Administrator     C:\Documents and Settings\Administrator\.ARIS70     C:\Documents and Settings\Administrator\.jindent     C:\Documents and Settings\Administrator\.nbi       C:\Documents and Settings\Administrator\.nbi\downloads       C:\Documents and Settings\Administrator\.nbi\log       C:\Documents and Settings\Administrator\.nbi\cache       C:\Documents and Settings\Administrator\.nbi\tmp       C:\Documents and Settings\Administrator\.nbi\wd     C:\Documents and Settings\Administrator\.netbeans       C:\Documents and Settings\Administrator\.netbeans\6.0 …

Note that the above program may crash with UnauthorizedAccessException in case you do not have access permissions for some folders on the hard disk. This is typical for some Windows installations so you could start the traversal from another directory to play with it, e.g. from "C:\Windows\assembly".

Breath-First-Search (BFS)

Let’s have a look at another way of traversing trees. Breath-First-Search (BFS) is an algorithm for traversing branched data structures (like trees and graphs). The BFS algorithm first traverses the start node, then all its direct children, then their direct children and so on. This approach is also known as the wavefront traversal, because it looks like the waves caused by a stone thrown into a lake.

The Breath-First-Search (BFS) algorithm consists of the following steps:

1.  Enqueue the start node in queue Q.

2.  While Q is not empty repeat the following two steps:

-    Dequeue the next node v from Q and print it.

-    Add all children of v in the queue.

The BFS algorithm is very simple and always traverses first the nodes that are closest to the start node, and then the more distant and so on until it reaches the furthest. The BFS algorithm is very widely used in problem solving, e.g. for finding the shortest path in a labyrinth.

A sample implementation of BFS algorithms that prints all folders in the file system is given below:

DirectoryTraverserBFS.cs

using System; using System.Collections.Generic; using System.IO;   /// <summary> /// Sample class, which traverses given directory /// based on the Breath-First-Search (BFS) algorithm /// </summary> public static class DirectoryTraverserBFS {     /// <summary>     /// Traverses and prints given directory with BFS     /// </summary>     /// <param name="directoryPath">the path to the directory         /// which should be traversed</param>     static void TraverseDir(string directoryPath)     {         Queue<DirectoryInfo> visitedDirsQueue =             new Queue<DirectoryInfo>();         visitedDirsQueue.Enqueue(new DirectoryInfo(directoryPath));         while (visitedDirsQueue.Count > 0)         {             DirectoryInfo currentDir = visitedDirsQueue.Dequeue();             Console.WriteLine(currentDir.FullName);               DirectoryInfo[] children = currentDir.GetDirectories();             foreach (DirectoryInfo child in children)             {                 visitedDirsQueue.Enqueue(child);             }         }     }       static void Main()     {         TraverseDir(@"C:\");     } }

If we start the program to traverse our local hard disk, we will see that the BFS first visits the directories closest to the root (depth 1), then the folders at depth 2, then depth 3 and so on. Here is a sample output of the program:

C:\ C:\Config.Msi C:\Documents and Settings C:\Inetpub C:\Program Files C:\RECYCLER C:\System Volume Information C:\WINDOWS C:\wmpub C:\Documents and Settings\Administrator C:\Documents and Settings\All Users C:\Documents and Settings\Default User …

Binary Trees

In the previous section we discussed the basic structure of a tree. In this section we will have a look at a specific type of tree – binary tree. This type of tree turns out to be very useful in programming. The terminology for trees is also valid about binary trees. Despite that below we will give some specific explanations about thus structure.

Binary Tree – a tree, which nodes have a degree equal or less than 2 or we can say that it is a tree with branching degree of 2. Because every node’s children are at most 2, we call them left child and right child. They are the roots of the left sub-tree and the right sub-tree of their parent node. Some nodes may have only left or only right child, not both. Some nodes may have no children and are called leaves.

Binary tree can be recursively defined as follows: a single node is a binary tree and can have left and right children which are also binary trees.

Binary Tree – Example

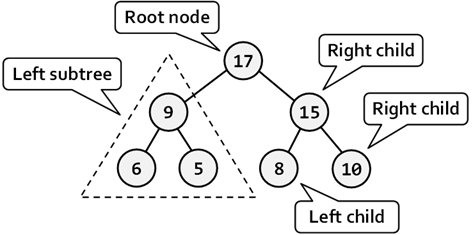
Here we have an example of binary tree. The nodes are again named with some numbers. An the figure we can see the root of the tree – "14", the left sub-tree (with root 19) and the right sub-tree (with root 15) and a right and left child – "3" and "21".

 

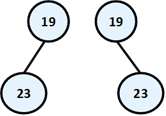
We have to note that there is one very big difference in the definition of binary tree from the definition of the classical tree – the order of the children of each node. The next example will illustrate that difference:

On this figure above two totally different binary trees are illustrated – the first one has root "19" and its left child "23" and the second root "19" and right child "23". If that was an ordinary tree they would have been the same. That’s why such tree we would illustrate the following way:

Remember! Although we take binary trees as a special case of a tree structure, we have to notice that the condition for particular order of children nodes makes them a completely different structure.

Binary Tree Traversal

The traversal of binary tree is a classic problem which has classical solutions. Generally there are few ways to traverse a binary tree recursively:

-     In-order (Left-Root-Right) – the traversal algorithm first traverses the left sub-tree, then the root and last the left sub-tree. In our example the sequence of such traversal is: "23", "19", "10", "6", "21", "14", "3", "15".

-     Pre-order (Root-Left-Right) – in this case the algorithm first traverses the root, then the left sub-tree and last the right sub-tree. The result of such traversal in our example is: "14", "19", "23", "6", "10", "21", "15", "3".

-     Post-order (Left-Right-Root) – here we first traverse the left sub-tree, then the right one and last the root. The result after the traversal is: "23", "10", "21", "6", "19", "3", "15", "14".

Recursive Traversal of Binary Tree – Example

The next example shows an implementation of binary tree, which we will traverse using the in-order recursive scheme.

using System; using System.Collections.Generic;   /// <summary>Represents a binary tree</summary> /// <typeparam name="T">Type of values in the tree</typeparam> public class BinaryTree<T> {     /// <summary>The value stored in the curent node</summary>     public T Value { get; set; }       /// <summary>The left child of the current node</summary>     public BinaryTree<T> LeftChild { get; private set; }       /// <summary>The right child of the current node</summary>     public BinaryTree<T> RightChild { get; private set; }         /// <summary>Constructs a binary tree</summary>     /// <param name="value">the value of the tree node</param>     /// <param name="leftChild">the left child of the tree</param>     /// <param name="rightChild">the right child of the tree     /// </param>     public BinaryTree(T value,         BinaryTree<T> leftChild, BinaryTree<T> rightChild)     {         this.Value = value;         this.LeftChild = leftChild;         this.RightChild = rightChild;     }       /// <summary>Constructs a binary tree with no children     /// </summary>     /// <param name="value">the value of the tree node</param>     public BinaryTree(T value) : this(value, null, null)     {     }       /// <summary>Traverses the binary tree in pre-order</summary>     public void PrintInOrder()     {         // 1. Visit the left child         if (this.LeftChild != null)         {             this.LeftChild.PrintInOrder();         }           // 2. Visit the root of this sub-tree         Console.Write(this.Value + " ");           // 3. Visit the right child         if (this.RightChild != null)         {             this.RightChild.PrintInOrder();         }     } }   /// <summary> /// Demonstrates how the BinaryTree<T> class can be used /// </summary> public class BinaryTreeExample {     static void Main()     {         // Create the binary tree from the sample         BinaryTree<int> binaryTree =             new BinaryTree<int>(14,                     new BinaryTree<int>(19,                           new BinaryTree<int>(23),                           new BinaryTree<int>(6,                                   new BinaryTree<int>(10),                                   new BinaryTree<int>(21))),                     new BinaryTree<int>(15,                           new BinaryTree<int>(3),                           null));           // Traverse and print the tree in in-order manner         binaryTree.PrintInOrder();         Console.WriteLine();           // Console output:         // 23 19 10 6 21 14 3 15     } }

How Does the Example Work?

This implementation of binary tree is slightly different from the one of the ordinary tree and is significantly simplified.

We have a recursive class definition BinaryTree<T>, which holds a value and left and right child nodes which are of the same type BinaryTree<T>. We have exactly two child nodes (left and right) instead of list of children.

The method PrintInOrder() works recursively using the DFS algorithm. It traverses each node in "in-order" (first the left child, then the node itself, then the right child). The DFS traversal algorithm performs the following steps:

1.  Recursive call to traverse the left sub-tree of the given node.

2.  Traverse the node itself (print its value).

3.  Recursive call to traverse the right sub-tree.

We highly recommend the reader to try and modify the algorithm and the source code of the given example to implement the other types of binary tree traversal of binary (pre-order and post-order) and see the difference.

Ordered Binary Search Trees

Till this moment we have seen how we can build traditional and binary trees. These structures are very summarized in themselves and it will be difficult for us to use them for a bigger project. Practically, in computer science special and programming variants of binary and ordinary trees are used that have certain special characteristics, like order, minimal depth and others. Let's review the most important trees used in programming.

As examples for a useful properties we can give the ability to quickly search of an element by given value (Red-Black tree); order of the elements in the tree (ordered search trees); balanced depth (balanced trees); possibility to store an ordered tree in a persistent storage so that searching of an element to be fast with as little as possible read operations (B-tree), etc.

In this chapter we will take a look at a more specific class of binary trees – ordered trees. They use one often met property of the nodes in the binary trees – unique identification key in every node. Important property of these keys is that they are comparable. Important kind of ordered trees are the so called "balanced search trees".

Comparability between Objects

Before continuing, we will introduce the following definition, which we will need for the further exposure.

Comparability – we call two objects A and B comparable, if exactly one of following three dependencies exists:

-     "A is less than B"

-     "A is bigger than B"

-     "A is equal to B"

Similarly we will call two keys A and B comparable, if exactly one of the following three possibilities is true: A < B, A > B or A = B.

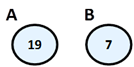
The nodes of a tree can contain different fields but we can think about only their unique keys, which we want to be comparable. Let’s give an example. We have two specific nodes A and B:

In this case, the keys of A and B hold the integer numbers 19 and 7. From Mathematics we know that the integer numbers (unlike the complex numbers) are comparable, which according the above reasoning give us the right to use them as keys. That’s why we can say that “A is bigger than B”, because “19 is bigger than 17”.

Please notice! In this case the numbers depicted on the nodes are their unique identification keys and not like before, just some numbers.

And we arrive to the definition of the ordered binary search tree:

Ordered Binary Tree (binary search tree) is a binary tree, in which every node has a unique key, every two of the keys are comparable and the tree is organized in a way that for every node the following is satisfied:

-     All keys in the left sub-tree are smaller than its key.

-     All keys in the right sub-tree are bigger than its key.

Properties of the Ordered Binary Search Trees

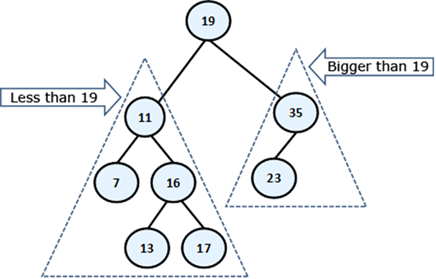
On the figure below we have given an example of an ordered binary search tree. We will use this example, to give some important properties of the binary tree’s order:

By definition we know that the left sub-tree of every node consists only of elements, which are smaller than itself, while in the right sub-tree there are only bigger elements. This means that if we want to find a given element, starting from the root, either we have found it or should search it respectively in its left or its right sub-tree, which will save unnecessary comparisons. For example, if we search 23 in our tree, we are not going to search for it in the left sub-tree of 19, because 23 is not there for sure (23 is bigger than 19, so eventually it is in the right sub-tree). This saves us 5 unnecessary comparisons with each of the left sub-tree elements, but if we were using a linked list, we would have to make these 5 comparisons.

From the elements’ order follows that the smallest element in the tree is the leftmost successor of the root, if there is such or the root itself, if it does not have a left successor. In our example this is the minimal element 7 and the maximal – 35. Next useful property from this is, that every single element from the left sub-tree of given node is smaller than every single element from the right sub-tree of the same node.

Ordered Binary Search Trees – Example

The next example shows a simple implementation of a binary search tree. Our point is to suggest methods for adding, searching and removing an element in the tree. For every single operation from the above, we will give an explanation in details. Note that our binary search tree is not balanced and may have poor performance in certain circumstances.

Ordered Binary Search Trees: Implementation of the Nodes

Just like before, now we will define an internal class, which will describe a node’s structure. Thus we will clearly distinguish and encapsulate the structure of a node, which our tree will contain within itself. This separate class BinaryTreeNode<T> that we have defined as internal is visible only in the ordered tree’s class.

Here is its definition:

BinaryTreeNode.cs

… /// <summary>Represents a binary tree node</summary> /// <typeparam name="T">Specifies the type for the values /// in the nodes</typeparam> internal class BinaryTreeNode<T> :     IComparable<BinaryTreeNode<T>> where T : IComparable<T> {     // Contains the value of the node     internal T value;       // Contains the parent of the node     internal BinaryTreeNode<T> parent;       // Contains the left child of the node     internal BinaryTreeNode<T> leftChild;       // Contains the right child of the node     internal BinaryTreeNode<T> rightChild;       /// <summary>Constructs the tree node</summary>     /// <param name="value">The value of the tree node</param>     public BinaryTreeNode(T value)     {         if (value == null)         {             // Null values cannot be compared -> do not allow them             throw new ArgumentNullException(                 "Cannot insert null value!");         }           this.value = value;         this.parent = null;         this.leftChild = null;         this.rightChild = null;     }       public override string ToString()     {         return this.value.ToString();     }       public override int GetHashCode()     {         return this.value.GetHashCode();     }       public override bool Equals(object obj)     {         BinaryTreeNode<T> other = (BinaryTreeNode<T>)obj;         return this.CompareTo(other) == 0;     }       public int CompareTo(BinaryTreeNode<T> other)     {         return this.value.CompareTo(other.value);     } } …

Let’s have a look to the proposed code. Still in the name of the structure, which we are considering – “ordered search tree”, we are talking about order and we can achieve this order only if we have comparability among the elements in the tree.

Comparability between Objects in C#

What does “comparability between objects” mean for us as developers? It means that we must somehow oblige everyone who uses our data structure, to create it passing it a type, which is comparable.

In C# the sentence “type, which is comparable” will sound like this:

T : IComparable<T>

The interface IComparable<T>, located in the namespace System, specifies the method CompareTo(T obj), which returns a negative integer number, zero or a positive integer number respectively if the current object is less, equal or bigger than the one which is given to the method for comparing. Its definition looks approximately like this:

public interface IComparable<T> {     /// <summary>Compares the current object with another     /// object of the same type.</summary>     int CompareTo(T other); }

On one hand, the implementation of this interface by given class ensures us that its instances are comparable (more about interfaces in OOP can be found in the "Interfaces" section of the "Defining Classes" chapter).

On the other hand, we need those nodes, described by BinaryTreeNode<T> class to be comparable between them too. That is why it implements IComparable<T> too. As it is shown in the code, the implementation of IComparable<T> to the BinaryTreeNode<T> class calls the type T’s implementation internally.

In the code we have also implemented the methods Equals(Object obj) and GetHashCode() too. A good (recommended) practice is these two methods to be consistent in their behavior, i.e. when two objects are the same, then their hash-code is the same. As we will see in the chapter about hash tables, the opposite is not necessary at all. Similarly – the expected behavior of the Equals(Object obj) is to return true, exactly when CompareTo(T obj) returns 0.

It’s recommended to sync the work of Equals(Object obj), CompareTo(T obj) and GetHashCode() methods. This is their expected behavior and it will save you a lot of hard to find problems.

Till now, we have discussed the methods, suggested by our class. Now let’s see what fields it provides. They are respectively for value (the key) of type T parent – parent, left and right successor – leftChild and rightChild. The last three are of the type of the defining them class – BinaryTreeNode

Ordered Binary Trees – Implementation of the Main Class

Now, we go to the implementation of the class, describing an ordered binary tree – BinarySearchTree<T>. The tree by itself as a structure consists of a root node of type BinaryTreeNode<T>, which contains internally its successors – left and right. Internally they also contain their successors, thus recursively down until it reaches the leaves.

An important thing is the definition BinarySearchTree<T> where T : IComparable<T>. This constraint of the type T is necessary because of the requirement of our internal class, which works only with types, implementing IComparable<T>. Due to this restriction we can use BinarySearchTree<int> and BinarySearchTree<string>, but cannot use BinarySearchTree<int[]> and BinarySearchTree<StreamReader>, because int[] and StreamReader are not comparable, while int and string are.

BinarySearchTree.cs

public class BinarySearchTree<T>    where T : IComparable<T> {     /// <summary>     /// Represents a binary tree node     /// </summary>     /// <typeparam name="T">The type of the nodes</typeparam>     internal class BinaryTreeNode<T> :         IComparable<BinaryTreeNode<T>> where T : IComparable<T>     {         // …         // … The implementation from above comes here!!! …         // …     }       /// <summary>     /// The root of the tree     /// </summary>     private BinaryTreeNode<T> root;       /// <summary>     /// Constructs the tree     /// </summary>     public BinarySearchTree()     {         this.root = null;     }       // …     // … The implementation of tree operations come here!!! …     // … }

As we mentioned above, now we will examine the following operations:

-     insert an element;

-     searching for an element;

-     removing an element.

Inserting an Element

Inserting (or adding) an element in a binary search tree means to put a new element somewhere in the tree so that the tree must stay ordered. Here is the algorithm: if the tree is empty, we add the new element as a root. Otherwise:

-     If the element is smaller than the root, we call recursively the same method to add the element in the left sub-tree.

-     If the element is bigger than the root, we call recursively to the same method to add the element in the right sub-tree.

-     If the element is equal to the root, we don’t do anything and exit from the recursion.

We can clearly see how the algorithm for inserting a node, conforms to the rule “elements in the left sub-tree are less than the root and the elements in the right sub-tree are bigger than the root”. Here is a sample implementation of this method. You should notice that in the addition there is a reference to the parent, which is supported because the parent must be changed too.

/// <summary>Inserts new value in the binary search tree /// </summary> /// <param name="value">the value to be inserted</param> public void Insert(T value) {     this.root = Insert(value, null, root); }   /// <summary> /// Inserts node in the binary search tree by given value /// </summary> /// <param name="value">the new value</param> /// <param name="parentNode">the parent of the new node</param> /// <param name="node">current node</param> /// <returns>the inserted node</returns> private BinaryTreeNode<T> Insert(T value,         BinaryTreeNode<T> parentNode, BinaryTreeNode<T> node) {     if (node == null)     {         node = new BinaryTreeNode<T>(value);         node.parent = parentNode;     }     else     {         int compareTo = value.CompareTo(node.value);         if (compareTo < 0)         {             node.leftChild =                 Insert(value, node, node.leftChild);         }         else if (compareTo > 0)         {             node.rightChild =                 Insert(value, node, node.rightChild);         }     }       return node; }

Searching for an Element

Searching in a binary search tree is an operation which is more intuitive. In the sample code we have shown how the search of an element can be done without recursion and with iteration instead. The algorithm starts with element node, pointing to the root. After that we do the following:

-     If the element is equal to node, we have found the searched element and return it.

-     If the element is smaller than node, we assign to node its left successor, i.e. we continue the searching in the left sub-tree.

-     If the element is bigger than node, we assign to node its right successor, i.e. we continue the searching in the right sub-tree.

At the end, the algorithm returns the found node or null if there is no such node in the tree. Additionally we define a Boolean method that checks if certain value belongs to the tree. Here is the sample code:

/// <summary>Finds a given value in the tree and /// return the node which contains it if such exsists /// </summary> /// <param name="value">the value to be found</param> /// <returns>the found node or null if not found</returns> private BinaryTreeNode<T> Find(T value) {     BinaryTreeNode<T> node = this.root;     while (node != null)     {         int compareTo = value.CompareTo(node.value);         if (compareTo < 0)         {             node = node.leftChild;         }         else if (compareTo > 0)         {             node = node.rightChild;         }         else         {             break;         }     }       return node; }   /// <summary>Returns whether given value exists in the tree /// </summary> /// <param name="value">the value to be checked</param> /// <returns>true if the value is found in the tree</returns> public bool Contains(T value) {     bool found = this.Find(value) != null;     return found; }

Removing an Element

Removing is the most complicated operation from the basic binary search tree operations. After it the tree must keep its order.

The first step before we remove an element from the tree is to find it. We already know how it happens. After that, we have 3 cases:

-     If the node is a leaf – we point its parent’s reference to null. If the element has no parent, it means that it is a root and we just remove it.

-     If the node has only one sub-tree – left or right, it is replacing with the root of this sub-tree.

-     The node has two sub-trees. Then we have to find the smallest node in the right sub-tree and swap with it. After this exchange the node will have one sub-tree at most and then we remove it grounded on some of the above two rules. Here we have to say that it can be done analogical swap, just that we get the left sub-tree and it is the biggest element.

We leave to the reader to check the correctness of these three steps, as a little exercise.

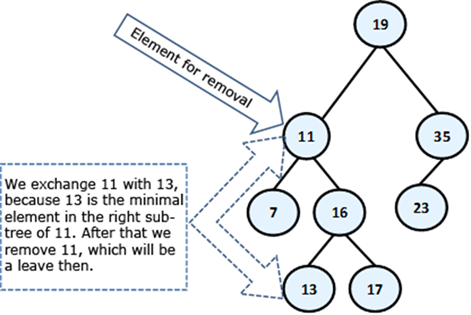
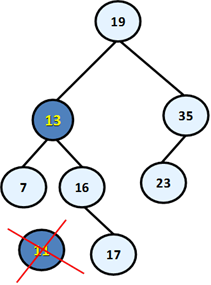
Now, let’s see a sample removal in action. Again we will use our ordered tree, which we have displayed at the beginning of this point. For example, let’s remove the element with key 11.

The node 11 has two sub-trees and according to our algorithm, it must be exchanged with the smallest element from the right sub-tree, i.e. with 13. After the exchange, we can remove 11 (it is a leaf). Here is the final result:

Below is the sample code, which implements the described algorithm:

/// <summary>Removes an element from the tree if exists /// </summary> /// <param name="value">the value to be deleted</param> public void Remove(T value) {     BinaryTreeNode<T> nodeToDelete = Find(value);     if (nodeToDelete != null)     {         Remove(nodeToDelete);     } }   private void Remove(BinaryTreeNode<T> node) {     // Case 3: If the node has two children.     // Note that if we get here at the end     // the node will be with at most one child     if (node.leftChild != null && node.rightChild != null)     {         BinaryTreeNode<T> replacement = node.rightChild;         while (replacement.leftChild != null)         {             replacement = replacement.leftChild;         }         node.value = replacement.value;         node = replacement;     }       // Case 1 and 2: If the node has at most one child     BinaryTreeNode<T> theChild = node.leftChild != null ?             node.leftChild : node.rightChild;       // If the element to be deleted has one child     if (theChild != null)     {         theChild.parent = node.parent;           // Handle the case when the element is the root         if (node.parent == null)         {             root = theChild;         }         else         {             // Replace the element with its child sub-tree             if (node.parent.leftChild == node)             {                 node.parent.leftChild = theChild;             }             else             {                 node.parent.rightChild = theChild;             }         }     }     else     {         // Handle the case when the element is the root         if (node.parent == null)         {             root = null;         }         else         {             // Remove the element - it is a leaf             if (node.parent.leftChild == node)             {                 node.parent.leftChild = null;             }             else             {                 node.parent.rightChild = null;             }         }     } }

We add also a DFS traversal method to enable printing the values stored in the tree in ascending order (in-order):

/// <summary>Traverses and prints the tree</summary> public void PrintTreeDFS() {     PrintTreeDFS(this.root);     Console.WriteLine(); }   /// <summary>Traverses and prints the ordered binary search tree /// tree starting from given root node.</summary> /// <param name="node">the starting node</param> private void PrintTreeDFS(BinaryTreeNode<T> node) {     if (node != null)     {         PrintTreeDFS(node.leftChild);         Console.Write(node.value + " ");         PrintTreeDFS(node.rightChild);     } }

Finally we demonstrate our ordered binary search tree in action:

class BinarySearchTreeExample {     static void Main()     {         BinarySearchTree<string> tree =             new BinarySearchTree<string>();         tree.Insert("Telerik");         tree.Insert("Google");         tree.Insert("Microsoft");         tree.PrintTreeDFS(); // Google Microsoft Telerik         Console.WriteLine(tree.Contains("Telerik")); // True         Console.WriteLine(tree.Contains("IBM")); // False         tree.Remove("Telerik");         Console.WriteLine(tree.Contains("Telerik")); // False         tree.PrintTreeDFS(); // Google Microsoft     } }

Note that when we print our binary search tree, it is always sorted in ascending order (in our case in alphabetical order). Thus in our example the binary search tree of strings behaves like a set of strings (we will explain the "Set" data structure in the chapter "Dictionaries, Hash Tables and Sets").

It is important to know that our class BinarySearchTree<T> implements a binary search tree, but not balanced / self-balancing binary search tree. Although it works correctly, its performance can be poor in certain circumstances, like we shall explain in the next section. Balanced trees are more complex concept and use more complex algorithm which guarantees their balanced depth. Let’s take a look at them.

Balanced Trees

As we have seen above, the ordered binary trees are a very comfortable structure to search within. Defined in this way, the operations for creating and deleting the tree have a hidden flaw: they don't balance the tree and its depth could become very big.

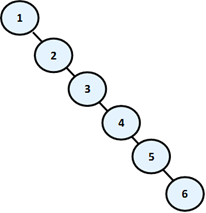
Think a bit what will happen if we sequentially include the elements: 1, 2, 3, 4, 5, 6? The ordered binary tree will look like this:

In this case, the binary tree degenerates into a linked list. Because of this the searching in this tree is going to be much slower (with N steps, not with log(N)), as to check whether an item is inside, in the worst case we will have to go through all elements.

We will briefly mention the existence of data structures, which save the logarithmic behavior of the operations adding, searching and removing an element in the common case. We will introduce to you the following definitions before we go on to explain how they are achieved:

Balanced binary tree – a binary tree in which no leaf is at “much greater” depth than any other leaf. The definition of “much greater” is rough depends on the specific balancing scheme.

Perfectly balanced binary tree – binary tree in which the difference in the left and right tree nodes’ count of any node is at most one.

Without going in details we will mention that when given binary search tree is balanced, even not perfectly balanced, then the operations of adding, searching and removing an element in it will run in approximately a logarithmic number of steps even in the worst case. To avoid imbalance in the tree to search, apply operations that rearrange some elements of the tree when adding or removing an item from it. These operations are called rotations in most of the cases. The type of rotation should be further specified and depends on the implementation of the specific data structure. As examples for structures like these we can give Red-Black tree, AVL-tree, AA-tree, Splay-tree and others.

Balanced search trees allow quickly (in general case for approximately log(n) number of steps) to perform the operations like searching, adding and deleting of elements. This is due to two main reasons:

-     Balanced search trees keep their elements ordered internally.

-     Balanced search trees keep themselves balanced, i.e. their depth is always in order of log(n).

Due to their importance in computer science we will talk about balanced search trees and their standard implementations in .NET Framework many times when we discuss data structures and their performance in this chapter and in the next few chapters.

Balanced search trees can be binary or non-binary.

Balanced binary search trees have multiple implementations like Red-Black Trees, AA Trees and AVL Trees. All of them are ordered, balanced and binary, so they perform insert / search / delete operations very fast.

Non-binary balanced search trees also have multiple implementations with different special properties. Examples are B-Trees, B+ Trees and Interval Trees. All of them are ordered, balanced, but not binary. Their nodes can typically hold more than one key and can have more than two child nodes. These trees also perform operations like insert / search / delete very fast.

For a more detailed examination of these and other structures we recommend the reader to look closely at literature about algorithms and data structures.

The Hidden Class TreeSet<T> in .NET Framework

Once we have seen ordered binary trees and seen what their advantage is comes the time to show and what C# has ready for us concerning them. Perhaps each of you secretly hoped that he / she will never have to implement a balanced ordered binary search tree, because it looks quite complicated.

So far we have looked at what balanced trees are to get an idea about them. When you need to use them, you can always count on getting them from somewhere already implemented. In the standard libraries of the .NET Framework there are ready implementations of balanced trees, but also on the Internet you can find a lot of external libraries.

In the namespace System.Collections.Generic a class TreeSet<T> exists, which is an implementation of a red-black tree. This, as we know, means that adding, searching and deleting items in the tree will be made with logarithmic complexity (i.e. if we have one million items operation will be performed for about 20 steps). The bad news is that this class is internal and it is visible only in this library. Fortunately, this class is used internally by a class, which is publicly available – SortedDictionary<T>. More info about the SortedDictionary<T> class you can find in the section "Sets" of chapter "Dictionaries, Hash-Tables and Sets".

Graphs

The graphs are very useful and fairly common data structures. They are used to describe a wide variety of relationships between objects and in practice can be related to almost everything. As we will see later, trees are a subset of the graphs and also lists are special cases of trees and thus of graphs, i.e. the graphs represent a generalized structure that allows modeling of very large set of real-world situations.

Frequent use of graphs in practice has led to extensive research in "graph theory", in which there is a large number of known problems for graphs and for most of them there are well-known solutions.

Graphs – Basic Concepts

In this section we will introduce some of the important concepts and definitions. Some of them are similar to those introduced about the tree data structure, but as we shall see, there are very serious differences, because trees are just special cases of graphs.

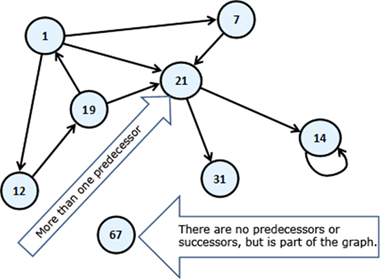
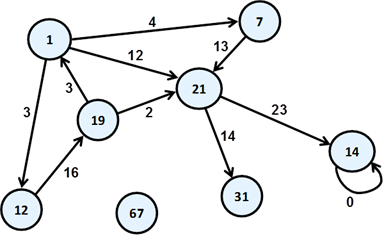
Let’s consider the following sample graph (which we would later call a finite and oriented). Again, like with trees, we have numbered the graph, as it is easier to talk about any of them specifically:

The circles of this scheme we will call vertices (nodes) and the arrows connecting them we will call directed edges. The vertex of which the arrow comes out we will call predecessor of that the arrow points. For example “19” is a predecessor of “1”. In this case, “1” is a successor of “19”. Unlike the structure tree, here each vertex can have more than one predecessor. Like “21”, it has three – “19”, “1” and “7”. If two of the vertices are connected with edge, then we say these two vertices are adjacent through this edge.

Next follows the definition of finite directed graph.

Finite directed graph is called the couple (V, E), in which V is a finite set of vertices and E is a finite set of directed edges. Each edge e that belongs to E is an ordered couple of vertices u and v or e = (u, v), which are defining it in a unique way.

For better understanding of this definition we are strongly recommending to the reader to think of the vertices as they are cities, and the directed edges as one-way roads. That way, if one of the vertices is Sofia and the other is Paris, the one-way path (edge) will be called Sofia – Paris. In fact this is one of the classic examples for the use of the graphs – in tasks with paths.

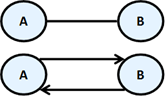
If instead of arrows, the vertices are connected with segments, then the segments will be called undirected edges, and the graph – undirected. Practically we can imagine that an undirected edge from vertex A to vertex B is two-way edge and equivalent to two opposite directed edges between the same two vertices:

Two vertices connected with an edge are called neighbors (adjacent).

For the edges a weight function can be assigned, that associates each edge to a real number. These numbers we will call weights (costs). For examples of the weights we can mention some distance between neighboring cities, or the length of the directed connections between two neighboring cities, or the crossing function of a pipe, etc. A graph that has weights on the edges is called weighted. Here is how it is illustrated a weighted graph.

Path in a graph is a sequence of vertices v₁, v₂, …, v_n,, such as there is an edge from v_i to v_i+1 for every i from 1 to n-1. In our example path is the sequence "1", "12", "19", "21". "7", "21" and "1" is not a path because there is no edge starting from "21" and ending in "1".

Length of path is the number of edges connecting vertices in the sequence of the vertices in the path. This number is equal to the number of vertices in the path minus one. The length of our example for path "1", "12", "19", "21" is three.

Cost of path in a weighted graph, we call the sum of the weights (costs) of the edges involved in the path. In real life the road from Sofia to Madrid, for example, is equal to the length of the road from Sofia to Paris plus the length of the road from Madrid to Paris. In our example, the length of the path "1", "12", "19" and "21" is equal to 3 + 16 + 2 = 21.

Loop is a path in which the initial and the final vertex of the path match. Example of vertices forming loop are "1", "12" and "19". In the same time "1", "7" and "21" do not form a loop.

Looping edge we will call an edge, which starts and ends in the same vertex. In our example the vertex "14" is looped.

A connected undirected graph we call an undirected graph in which there is a path from each node to each other. For example, the following graph is not connected because there is no path from "1" to "7".

So we already have enough knowledge to define the concept tree in other way, as a special kind of graph:

Tree – undirected connected graph without loops.

As a small exercise we let the reader show why all definitions of tree we gave in this chapter are equivalent.

Graphs – Presentations

There are a lot of different ways to present a graph in the computer programming. Different representations have different properties and what exactly should be selected depends on the particular algorithm that we want to apply. In other words – we present the graph in a way, so that the operations that our algorithm does on it to be as fast as possible. Without falling into greater details we will set out some of the most common representations of graphs.

-    List of successors – in this representation for each vertex v a list of successor vertices is kept (like the tree’s child nodes). Here again, if the graph is weighted, then to each element of the list of successors an additional field is added indicating the weight of the edge to it.

-    Adjacency matrix – the graph is represented as a square matrix g[N][N], where if there is an edge from v_i to v_j, then the position g[i][j] is contains the value 1. If such an edge does not exist, the field g[i][j] is contains the value 0. If the graph is weighted, in the position g[i][j] we record weight of the edge, and matrix is called a matrix of weights. If between two nodes in this matrix there is no edge, then it is recorded a special value meaning infinity. If the graph is undirected, the adjacency matrix will be symmetrical.

-     List of the edges – it is represented through the list of ordered pairs (v_i, v_j), where there is an edge from v_i to v_j. If the graph is weighted, instead ordered pair we have ordered triple, and its third element shows what the weight of the edge is.

-     Matrix of incidence between vertices and edges – in this case, again we are using a matrix but with dimensions g[M][N], where N is the number of vertices, and M is the number of edges. Each column represents one edge, and each row a vertex. Then the column corresponding to the edge (v_i, v_j) will contain 1 only at position i and position j, and other items in this column will contain 0. If the edge is a loop, i.e. is (v_i, v_i), then on position i we record 2. If the graph we want to represent is oriented and we want to introduce edge from v_i to v_j, then to position i we write 1 and to the position j we write -1.

The most commonly used representation of graphs is the list of successors.

Graphs – Basic Operations

The basic operations in a graph are:

-     Creating a graph

-     Adding / removing a vertex / edge

-     Check whether an edge exists between two vertices

-     Finding the successors of given vertex

We will offer a sample implementation of the graph representation with a list of successors and we will show how to perform most of the operations. This kind of implementation is good when the most often operation we need is to get the list of all successors (child nodes) for a certain vertex. This graph representation needs a memory of order N + M where N is the number of vertices and M is the number of edges in the graph.

In essence the vertices are numbered from 0 to N-1 and our Graph class holds for each vertex a list of the numbers of all its child vertices. It does not work with the nodes, but with their numbers in the range [0...N-1]. Let’s explore the source code of our sample graph:

using System; using System.Collections.Generic;   /// <summary>Represents a directed unweighted graph structure /// </summary> public class Graph {     // Contains the child nodes for each vertex of the graph     // assuming that the vertices are numbered 0 ... Size-1     private List<int>[] childNodes;       /// <summary>Constructs an empty graph of given size</summary>     /// <param name="size">number of vertices</param>     public Graph(int size)     {         this.childNodes = new List<int>[size];         for (int i = 0; i < size; i++)         {             // Assing an empty list of adjacents for each vertex             this.childNodes[i] = new List<int>();         }     }       /// <summary>Constructs a graph by given list of     /// child nodes (successors) for each vertex</summary>     /// <param name="childNodes">children for each node</param>     public Graph(List<int>[] childNodes)     {         this.childNodes = childNodes;     }       /// <summary>     /// Returns the size of the graph (number of vertices)     /// </summary>     public int Size     {         get { return this.childNodes.Length; }     }       /// <summary>Adds new edge from u to v</summary>     /// <param name="u">the starting vertex</param>     /// <param name="v">the ending vertex</param>     public void AddEdge(int u, int v)     {         childNodes[u].Add(v);     }       /// <summary>Removes the edge from u to v if such exists     /// </summary>     /// <param name="u">the starting vertex</param>     /// <param name="v">the ending vertex</param>     public void RemoveEdge(int u, int v)     {         childNodes[u].Remove(v);     }       /// <summary>     /// Checks whether there is an edge between vertex u and v     /// </summary>     /// <param name="u">the starting vertex</param>     /// <param name="v">the ending vertex</param>     /// <returns>true if there is an edge between     /// vertex u and vertex v</returns>     public bool HasEdge(int u, int v)     {         bool hasEdge = childNodes[u].Contains(v);         return hasEdge;     }       /// <summary>Returns the successors of a given vertex     /// </summary>     /// <param name="v">the vertex</param>     /// <returns>list of all successors of vertex v</returns>     public IList<int> GetSuccessors(int v)     {         return childNodes[v];     } }

To illustrate how our graph data structure works, we will create small program that creates a graph and traverses it by the DFS algorithm. To play a bit with graphs, the goal of our graph traversal algorithm will be to count how many connected components the graph has.

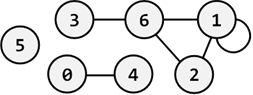
By definition in undirected graph if a path exists between two nodes, they belong to the same connected component and if no path exists between two nodes, they belong to different connected components. For example consider the following undirected graph:

It has 3 connected components: {0, 4}, {1, 2, 6, 3} and {5}.

The code below creates a graph corresponding to the figure above and by DFS traversal finds all its connected components. This is straightforward: pass through all vertices and once unvisited vertex is found, all connected to it vertices (directly or indirectly via some a path) are found by DFS traversal, each of them is printed and marked as visited. Below is the code:

class GraphComponents {     static Graph graph = new Graph(new List<int>[] {         new List<int>() {4},     // successors of vertice 0         new List<int>() {1, 2, 6}, // successors of vertice 1         new List<int>() {1, 6},    // successors of vertice 2         new List<int>() {6},     // successors of vertice 3         new List<int>() {0},     // successors of vertice 4         new List<int>() {},      // successors of vertice 5         new List<int>() {1, 2, 3}  // successors of vertice 6     });       static bool[] visited = new bool[graph.Size];       static void TraverseDFS(int v)     {         if (!visited[v])         {             Console.Write(v + " ");             visited[v] = true;             foreach (int child in graph.GetSuccessors(v))             {                 TraverseDFS(child);             }         }     }       static void Main()     {         Console.WriteLine("Connected graph components: ");         for (int v = 0; v < graph.Size; v++)         {             if (!visited[v])             {                 TraverseDFS(v);                 Console.WriteLine();             }         }     } }

If we run the above code, we will get the following output (the connected components of our sample graph shown above):

Connected graph components: 0 4 1 2 6 3 5

Common Graph Applications

Graphs are used to model many situations of reality, and tasks on graphs model multiple real problems that often need to be resolved. We will give just a few examples:

-     Map of a city can be modeled by a weighted oriented graph. On each street, edge is compared with a length, corresponding to the length of the street, and direction – the direction of movement. If the street is a two-way, it can be compared to two edges in both directions. At each intersection there is a node. In such a model there are natural tasks such as searching for the shortest path between two intersections, checking whether there is a road between two intersections, checking for a loop (if we can turn and go back to the starting position) searching for a path with a minimum number of turns, etc.

-     Computer network can be modeled by an undirected graph, whose vertices correspond to the computers in the network, and the edges correspond to the communication channels between the computers. To the edges different numbers can be compared, such as channel capacity or speed of the exchange, etc. Typical tasks for such models of a network are checking for connectivity between two computers, checking for double-connectivity between two points (existence of double-secured channel, which remains active after the failure of any computer), finding a minimal spanning tree (MST), etc. In particular, the Internet can be modeled as a graph, in which are solved problems for routing packets, which are modeled as classical graph problems.

-     The river system in a given region can be modeled by a weighted directed graph, where each river is composed of one or more edges, and each node represents the place where two or more rivers flow into another one. On the edges can be set values, related to the amount of water that goes through them. Naturally with this model there are tasks such as calculating the volume of water, passing through each vertex and anticipate of possible flood in increasing quantities.

You can see that the graphs can be used to solve many real-world problems. Hundreds of books and research papers are written about graphs, graph theory and graph algorithms. There are dozens of classic tasks for graphs, for which there are known solutions or it is known that there is no efficient solution. The scope of this chapter does not allow mentioning all of them, but we hope that through the short presentation we have awaken your interest in graphs, graph algorithms and their applications and spur you to take enough time to solve the tasks about graphs in the exercises.

Exercises

1.    Write a program that finds the number of occurrences of a number in a tree of numbers.

2.    Write a program that displays the roots of those sub-trees of a tree, which have exactly k nodes, where k is an integer.

3.    Write a program that finds the number of leaves and number of internal vertices of a tree.

4.    Write a program that finds in a binary tree of numbers the sum of the vertices of each level of the tree.

5.    Write a program that finds and prints all vertices of a binary tree, which have for only leaves successors.

6.    Write a program that checks whether a binary tree is perfectly balanced.

7.    Let’s have as given a graph G(V, E) and two of its vertices x and y. Write a program that finds the shortest path between two vertices measured in number of vertices staying on the path.

8.    Let’s have as given a graph G(V, E). Write a program that checks whether the graph is cyclic.

9.    Implement a recursive traversal in depth in an undirected graph and a program to test it.

10.   Write breadth first search (BFS), based on a queue, to traverse a directed graph.

11.   Write a program that searches the directory C:\Windows\ and all its subdirectories recursively and prints all the files which have extension *.exe.

12.   Define classes File {string name, int size} and Folder {string name, File[] files, Folder[] childFolders}. Using these classes, build a tree that contains all files and directories on your hard disk, starting from C:\Windows\. Write a method that calculates the sum of the sizes of files in a sub-tree and a program that tests this method. To crawl the directories use recursively crawl depth (DFS).

13.   * Write a program that finds all loops in a directed graph.

14.   Let’s have as given a graph G (V, E). Write a program that finds all connected components of the graph, i.e. finds all maximal connected sub-graphs. A maximal connected sub-graph of G is a connected graph such that no other connected sub-graphs of G, contains it.

15.   Suppose we are given a weighted oriented graph G (V, E), in which the weights on the side are nonnegative numbers. Write a program that by a given vertex x from the graph finds the shortest paths from it to all other vertical.

16.   We have N tasks to be performed successively. We are given a list of pairs of tasks for which the second is dependent on the outcome of the first and should be executed after it. Write a program that arranges tasks in such a way that each task is be performed after all the tasks which it depends on have been completed. If no such order exists print an appropriate message.

Example: {1, 2}, {2, 5}, {2, 4}, {3, 1} à 3, 1, 2, 5, 4

17.   An Eulerian cycle in a graph is called a loop that starts from a vertex, passes exactly once through all edges in the graph returns to the starting vertex. Vertices can be visited repeatedly. Write a program that by a given graph, finds whether the graph has an Euler loop.

18.   A Hamiltonian cycle in a graph is a cycle containing every vertex in the graph exactly once. Write a program, which by given weighted oriented graph G (V, E), finds Hamiltonian loop with a minimum length, if such exists.

Solutions and Guidelines

1.    Traverse the tree recursively in depth (using DFS) and count the occurrences of the given number.

2.    Traverse the tree recursively in depth (using DFS) and check for each node the given condition. For each node the number of nodes in its subtree is: 1 + the sum of the nodes of each of its child subtrees.

3.    You can solve the problem by traversing the tree in depth recursively.

4.    Use traversing in depth or breadth and when shifting from one node to another keep its level (depth). Knowing the levels of the nodes at each step, the wanted amount can be easily calculated.

5.    You can solve the problem by recursively traversing the tree in depth and by checking the given condition.

6.    By recursive traversal in depth (DFS) for every node of the tree calculate the depths of its left and right sub-trees. Then check immediately whether the condition of the definition for perfectly balanced tree is executed (check the difference between the left and right sub-tree’s depths).

7.    Use the algorithm of traversing in breadth (BFS) as a base. In the queue put every node always along with its predecessor. This will help you to restore the path between the nodes (in reverse order).

8.    Use traversing in depth or in breadth. Mark every node, if already visited. If at any time you reach to a node, which has already been visited, then you have found loop.

Think about how you can find and print the loop itself. Here is an idea: while traversing every node keep its predecessor. If at any moment you reach a node that has already been visited, you should have a path to the initial node. The current path in the recursion stack is also a path to the wanted node. So at some point we have two different paths from one node to the initial node. By merging the two paths you can easily find the loop.

9.    Use the DFS algorithm. Testing can be done with few example graphs.

10.   Use the BFS algorithm. Instead of putting the vertices of the graph in the queue, put their numbers (0 … N-1). This will simplify the algorithm.

11.   Use traversing in depth and System.IO.Directory class.

12.   Use the example of the tree data structure given in this chapter. Each directory from the tree should two arrays (or lists) of descendants: subdirectories and files.

13.   Use the solution of problem 8, but modify it so it does not stop when it finds a loop, but continues. For each loop you should check if you have already found it. This problem is more complex than you may expect!

14.   Use the algorithms for traversing in breadth or depth as a base.

15.   Use the Dijkstra’s algorithm (find it on the Internet).

16.   The requested order is called "topological sorting of a directed graph". It can be implemented in two ways:

For every task t we should know how many others tasks P(t) it depends on. We find task t₀, which is independent, i.e. P(t₀)=0 and we execute it. We reduce P(t) for every task, which depends from task t₀. Again we look for a task, which is independent and we execute it. We repeat until the tasks end or until we find a moment when there is no task t_k having P(t_k)=0. In the last case no solution exists due to a cyclic dependency.

We can solve the task with traversing the graph in depth and printing every node just before leaving it. That means that at any time of printing of a task, all the tasks that depend on it should have already been printed. The topological sorting will be produced in reversed order.

17.   The graph must be connected and the degree of each of its nodes must be even in order an Eulerian cycle in a graph to exits (can you prove this?). With series of DFS traversals you can find cycles in the graph and to remove the edges involved in them. Finally, by joining the cycles you will get the Eulerian cycle. See more about Eulerian paths and cycles at http://en.wikipedia.org/wiki/Eulerian_path.

18.   If you write a true solution of the problem, check whether it works for a graph with 200 nodes. Do not try to solve the problem so it could work with a large number of nodes! If someone manages to solve it for large numbers of nodes, he will remain permanently in history! See also the Wikipedia article http://en.wikipedia.org/wiki/Hamiltonian_path_problem. You might try some recursive algorithm for generating all paths but accept that it will be slow. Techniques like backtracking and branch and bound could help a bit but generally this problem is NP-complete and thus no efficient solution is known to exist for it.

Demonstrations (source code)

Download the demo examples for this chapter from the book: Trees-and-Graphs-Demos.zip.

Discussion Forum

Comment the book and the tasks in the : forum of the Software Academy.

Tags: .NET Framework self-balancing binary search, binary search trees, binary trees, building a model of real life problems, Common Graph Applications, graph, graph implementation, graphs, self-balancing binary search tree, tree data structures, trees, types of graphs