Chapter 18. Dictionaries, Hash-Tables and Sets
In this chapter we will analyze more complex data structures like dictionaries and sets, and their implementations with hash-tables and balanced trees. We will explain in more details what hashing and hash-tables mean and why they are such an important part of programming. We will discuss the concept of "collisions" and how they might happen when implementing hash-tables. Also we will offer you different types of approaches for solving this type of issues. We will look at the abstract data structure set and explain how it can be implemented with the ADTs dictionary and balanced search tree. Also we will provide you with examples that illustrate the behavior of these data structures with real world examples.
Content
- Video
- Presentation
- Mind Maps
- In This Chapter
- Dictionary Data Structure
- Hash-Tables
- The "Set" Data Structure
- Exercises
- Solutions and Guidelines
- Demonstrations (source code)
- Discussion Forum
Video
Presentation
Mind Maps
In the last few chapters we got familiar with some classic and very important data structures – arrays, lists, trees and graphs. In this chapter we will get familiar with the so called "dictionaries", which are extremely useful and widely used in the programming.
The dictionaries are also known as associative arrays or maps. In this book we are going to use the terminology "dictionary". Every element in the dictionary has a key and an associated value for this key. Both the key and the value represent a pair. The analogy with the real world dictionary comes from the fact, that in every dictionary, for every for word (key), we also have a description related to this word (value).
|
As well as the data (values), that the dictionary holds, there is also a key that is used for searching and finding the required values. The elements of the dictionary are represented by pairs (key, value), where the key is used for searching. |
Dictionary Data Structure – Example
We are going to illustrate what exactly the data structure dictionary means using an everyday, real world example.
When you go to a theatre, opera or a concert, there is usually a place where you can leave your outdoor clothing. The employee than takes your jacket and gives you a number. When the event is over, on your way out, you give them back the same number. The employee uses this number to search and find your jacket to give back to you.
Thanks to this example we can see that the idea for using a key (the number that the employee gives you) to store a value (your jacket), and later having the option to access it, is not so abstract. Actually this is a method that is often widely used not only in programming, but also in many other practical areas.
When using the ADT dictionary, the key may not just be a number, but any other type of object. In the case, when we have a key (number), we could implement this type of structure as a regular array. In this scenario the set of keys is already known – these are the numbers from 0 to n, where n represents the size of the array (when n is within the allowed limits). The idea of the dictionaries is to provide us with more flexibility regarding the set of the keys.
When using dictionaries, the set of keys usually is a randomly chosen set of values like real numbers or strings. The only restriction is that we can distinguish one key from the other. Later we will take a look at some additional requirements for the keys that are needed for the different kinds of implementations.
For every key in the dictionary, there is a corresponding value. One key can hold only one value. The aggregation of all the pairs (key, value) represents the dictionary.
Here is the first example for using a dictionary in .NET:
|
IDictionary<string, double> studentMarks =
studentMarks["Paul"] = 3.00; Console.WriteLine("Paul 's mark: {0:0.00}", studentMarks["Paul"]); |
Later in this chapter, we will find out the result from the execution of the example above.
The Abstract Data Structure “Dictionary” (Associative Array, Map)
In programming the abstract data structure "dictionary" is represented by many aggregated pairs (key, value) along with predefined methods for accessing the values by a given key. Alternatively this data structure can also be called a "map" or "associative array".
Described below are the required operations, defined by this data structure:
- void Add(K key, V value) – adds given key-value pair in the dictionary. With most implementations of this class in .NET, when adding a key that already exists, an exception is thrown.
- V Get(K key) – returns the value by the specified key. If there is no pair with this key, the method returns null or throws an exception depending on the specific dictionary implementation.
- bool Remove(key) – removes the value, associated with the specified key and returns a Boolean value, indicating if the operation was successful.
Here are some additional methods, which are supported by the ADT.
- bool Contains(key) – returns true if the dictionary has a pair with the selected key
- int Count – returns the number of elements (key value pairs) in the dictionary
Other operations that are usually supported are: extracting all of the keys, values or key value pairs and importing them into another structure (array, list). This way they can easily be traversed using a loop.
|
For the comfort of .NET developers, the IDictionary<K, V> interface holds an indexing property V this[K] { get; set; }, which is usually implemented by calling the methods V Get(K), Add(K, V). Bear in mind that the access method (accessor) get of the property V this[K] of the class Dictionary<K, V> in .NET throws an exception if the given key K does not exist in the dictionary. In order to access the value of a certain key, without having to worry about exceptions, use the method bool TryGetValue(K key, out V value). |
The Interface IDictionary<K, V>
In .NET there is a standard interface IDictionary<K, V> where K defines the type of the key, and V type of the value. It defines all of the basic operations that the dictionaries should implement. IDictionary<K, V> corresponds to the abstract data structure "dictionary" and defines the operations, mentioned above, but without supplying an actual implementation of them. This interface is defined in assembly mscorelib, namespace System.Collections.Generic.
In .NET interfaces represent specifications of methods for a certain class. They define methods without implementation, which should be implemented by the classes that inherit them. How the interfaces and inheritance work we will discuss in more details in the chapter "Principles of the Object-Oriented Programming". For the moment all you need to know is that interfaces define which methods and fields should be implemented in the classes that inherit the interface.
In this chapter we will take a look at the two most popular dictionary implementations – with a balanced tree and a hash-table. It’s extremely important for you to know how they differ from one another, and which are the main principles related to them. Otherwise you risk using them improperly and inefficiently.
In .NET Framework there are two major implementations of the interface IDictionary<K, V> – Dictionary<K, V> and SortedDictionary<K, V>. SortedDictionary is an implementation by a balanced (red-black) tree, and Dictionary – by a hash-table.
|
Except for IDictionary<K, V> in .NET there is one more interface – IDictionary, along with the classes implementing it: Hashtable, ListDictionary and HybridDictionary. They are heritage from the first version of .NET. These classes need to be used only on special occasions. Much more preferable is the use of Dictionary<K, V> or SortedDictionary<K, V>. |
In this and the next chapter we will analyze when the different implementations of dictionaries are used.
Implementation of Dictionary with Red-Black Tree
Because the implementation of a dictionary with a balanced tree is very extensive and complex task, we will not examine it in source code. Instead we will analyze the class SortedDictionary<K, V>, that comes with the standard .NET library. We strongly recommend the curious readers to look at the decompiled code of the SortedDictionary class using some of the decompilation tools mentioned in the chapter "Introduction to Programming" like JustDecompile.
As we mentioned in the previous chapter, a red-black tree is an ordered binary balanced search tree, that’s used for searching. This is why one of the important requirements for the set of keys used by SortedDictionary<K, V> is comparability. This means that, if we have two keys, either one of them should be bigger, or they should be equal. The keys used in SortedDictionary<K, V> should implement IComparable<K>.
The usage of the binary search tree gives us a great advantage: the keys in the dictionary are stored ordered. Thanks to this feature, if we need the data ordered by keys, we don’t need to perform any additional sorting. Actually, this is the only advantage of this dictionary implementation compared to the hash-table.
A thing that should be mentioned is that keeping the keys ordered comes with its price. Searching for the elements using in an ordered balanced tree is slower (typically takes log(n) steps) than using a hash-table (typical takes fixed number of steps). Because of this, if there is no requirement for the keys to be ordered, it’s better to use Dictionary<K, V>.
|
Use a balanced tree dictionary only when you need your pairs (key, value) to be ordered by key. Bear in mind that the balanced tree comes with the complexity of the algorithm log(n), for searching, adding and deleting elements. Compared to this, the complexity used in hash-table may reach a linear value. |
The Class SortedDictionary<K, V>
The class SortedDictionary<K, V> is a dictionary implementation, which uses a red-black tree. This class implements all the standard operations defined in the interface IDictionary<K, V>.
Using SortedDictionary Class – Example
Now we will solve a practical problem, where using the class SortedDictionary is a good idea. Let’s say we have arbitrary text. Our task would be to find all the different words in the text, and the number of occurrences of these words. Additionally we should print all the words found in alphabetical order.
For this task using a dictionary is a really good idea. We can use the different words in the text for keys, and the value for each key would be the number of occurrences for each word in our text.
The algorithm for counting the words is the following: we read the text word by word. For each word we check if it already exists in the dictionary. If the answer is no, we add a new element in the dictionary with a value of 1. If the answer is yes – we increase the old value of the element by one, so as to count the last occurrence.
The elements of the ordered dictionary SortedDictionary<string, int> will be ordered by their key during the iteration process. This way we met the additional requirement for the words to be ordered alphabetically. Below is a sample implementation of the described algorithm:
|
WordCountingWithSortedDictionary.cs |
|
using System; using System.Collections.Generic; class WordCountingWithSortedDictionary { private static readonly string Text = "Mary had a little lamb " + "little Lamb, little Lamb, " + "Mary had a Little lamb, " + "whose fleece were white as snow.";
static void Main() { IDictionary<String, int> wordOccurrenceMap = GetWordOccurrenceMap(Text); PrintWordOccurrenceCount(wordOccurrenceMap); }
private static IDictionary<string, int> GetWordOccurrenceMap( string text) { string[] tokens = text.Split(' ', '.', ',', '-', '?', '!');
IDictionary<string, int> words = new SortedDictionary<string, int>();
foreach (string word in tokens) { if (!string.IsNullOrEmpty(word.Trim())) { int count; if (!words.TryGetValue(word, out count)) { count = 0; } words[word] = count + 1; } } return words; }
private static void PrintWordOccurrenceCount( IDictionary<string, int> wordOccurenceMap) { foreach (var wordEntry in wordOccurenceMap) { Console.WriteLine( "Word '{0}' occurs {1} time(s) in the text", wordEntry.Key, wordEntry.Value); } } } |
The output from executing this code is the following:
|
Word 'a' occurs 2 time(s) in the text Word 'as' occurs 1 time(s) in the text Word 'fleece' occurs 1 time(s) in the text Word 'had' occurs 2 time(s) in the text Word 'lamb' occurs 2 time(s) in the text Word 'Lamb' occurs 2 time(s) in the text Word 'little' occurs 3 time(s) in the text Word 'Little' occurs 1 time(s) in the text Word 'mary' occurs 2 time(s) in the text Word 'snow' occurs 1 time(s) in the text Word 'was' occurs 1 time(s) in the text Word 'white' occurs 1 time(s) in the text Word 'whose' occurs 1 time(s) in the text |
Note that we are counting the words "little" and "lamb" starting with both lowercase and uppercase characters as different.
In this example, we demonstrated for the first time how to traverse a dictionary using the method PrintWordOccurrenceCount(IDictionary <string, int>). We used a foreach loop. When iterating through the elements of dictionaries, we need to take into account that the elements of this ADT are ordered pairs (key and value), not just single objects. Because IDictionary<K, V> implements the interface IEnumerable<KeyValuePair <K, V>>, this means that the foreach loop should iterate through objects of type KeyValuePair<K, V>. For simplicity we use the var-syntax in the foreach loop.
IComparable<K> Interface
When using SortedDictionary<K, V> the keys are required to be comparable. In our example we use objects of type string.
The class string implements the interface IComparable, and the comparison between the elements is done lexicographically. What does that mean? By default the strings in .NET are case sensitive (the compiler distinguishes uppercase from lowercase letters). Words like "Length" and "length" are considered different. This means that words that start with a lowercase letter will be before the ones with an uppercase letter. This definition comes from the implementation of the method CompareTo(object), through which the string class implements the interface IComparable.
IComparer<T> Interface
What should we do when we are not happy with the default implementation of comparison? For example, what should we do when we want uppercase and lowercase characters to be treated as equal?
One option we have is to transform the word into a capital, or non-capital string, but sometimes the situation is more complicated than that. This is why we will offer another solution, which works for every class that does not implement the IComparable<T> interface, or it does implement it, but we want to change its behavior.
For the comparison of objects with an exclusively defined order in SortedDictionary<K, V> in .NET, we will use the interface IComparer<T>. It defines a comparison function int Compare(T x, T y) that is an alternative to the already defined order. Let’s take a better look at this interface.
When we create an object of type SortedDictionary<K, V> we can pass to its constructor a reference to IComparer<K> so that it can use it for the key comparison (key elements should be objects of type K).
Here is a sample implementation of IComparer<K> that changes the behavior when comparing strings, so that they are not distinguished by uppercase and lowercase characters:
|
class CaseInsensitiveComparer : IComparer<string> { public int Compare(string s1, string s2) { return string.Compare(s1, s2, true); } } |
Let’s use this interface IComparer<E> when creating the dictionary:
|
IDictionary<string, int> words = new CaseInsensitiveComparer()); |
After changing this in the code, the result from the program execution will be:
|
Word 'a' occurs 2 time(s) in the text Word 'as' occurs 1 time(s) in the text Word 'fleece' occurs 1 time(s) in the text Word 'had' occurs 2 time(s) in the text Word 'lamb' occurs 4 time(s) in the text Word 'little' occurs 4 time(s) in the text … |
The first time a word is found, it becomes a key in the dictionary. This is because after calling the words[word] = count + 1 only the value is changed, and not the key itself.
After using IComparer<E> we changed the definition for ordering keys in our dictionary. If, for a key, we used a class, defined by us, for example – Student, that implements IComparable<E>, we would get the same result if we were to alter the method CompareTo(Student). There is also one additional requirement, when implementing IComparable<K>:
|
When two objects are equal (Equals(object) returns true), CompareTo(E) should return 0. |
Meeting this requirement would allow us to use the objects of a custom class as keys, just as in the implementation with a balanced tree (SortedDictionary<K,V>, constructed without Comparer), as well with a hash-table (Dictionary<K,V>).
Now let’s get familiar with the data structure hash-table, which implements the abstract data structure dictionary in a very efficient way. We well explain in details how hash-tables actually work and why they are so efficient.
Dictionary Implementation with Hash-Table
With a hash-table implementation, the time for accessing the elements in the dictionary is theoretically independent from their count. This is a very important advantage.
Let’s make a comparison between list and hash-table in the speed of searching. We take a list of randomly ordered elements. We want to check if a certain element is in the list. The worst case scenario is to check every element in the list, so as to give an explicit answer to the question “Does this list contain the element or not”. It’s obvious that the number of checks would depend (linear) of the number of elements.
With hash-tables, if we have a key, the number of comparisons that we would need to do to find out if there is a key with this value, is constant and it does not depend on the number of elements. How exactly we are achieving such efficiency, we will explain in more details below.
What is a Hash-Table?
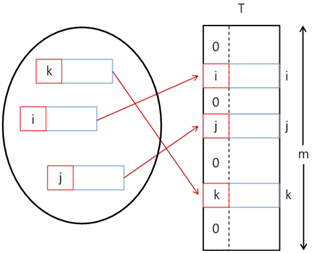
The data structure hash-table is usually implemented internally with an array. It consists of numerated elements (cells), each either holding a key-value pair or is empty (null). This at first sight, look like as if the elements were randomly placed in the array. At the positions that we don’t have an ordered pair, we have an empty element (null). The figure below illustrates how a hash-table might look like:
The size of the internal storage array of the hash-table is called capacity. The load factor is a real number between 0 and 1, which stands for the ratio between the occupied elements and the current capacity. At the figure we have a hash-table with 3 elements and capacity m. The load factor for this hash-table would be 3/m.
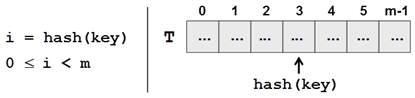
When adding or searching for elements, a method for hashing the key (hash function) is executed hash(key), that returns a number we call a hash-code. When we take the division remainder of this hash-code and the capacity m we get a number between 0 and m-1:
|
index = hash(key) % m |
At the figure there is a hash-table T with capacity m and hash-function hash(key):
This value hash(k) gives us the position in the array at which we search or add a certain key-value pair having this k. If the hash-function distributes the keys uniformly, in most cases for every key a different hash value will be assigned. In this way every cell of the array will have at most one key. Ultimately we get an extremely fast search and insertion of the elements: just calculate the hash function and obtain the cell assigned for the key. Of course it may occur that different keys would have the same hash code. We will examine this special case in more details later.
|
Use implementation of dictionary based on hash-table, when you need to find values by key with a maximum speed. |
The internal table’s capacity is increased when the number of elements in the hash-table becomes greater or equal to a certain constant called fill factor (load factor, the maximal degree of filling). When increasing the capacity (usually doubling it), all of the elements are reordered by the hash code of their keys and their assigned cell is calculated according to the new capacity. The load factor is significantly decreased after the reordering. This operation is time-consuming, but it is executed relatively rare, so it will not impact the overall performance of the "add" operation.
Before we go further with the theory of hash-tables, let’s review how hash-tables are implemented in C# and .NET Framework.
Class Dictionary <K, V>
The class Dictionary<K, V> is a standard implementation of a dictionary based on hash-table in .NET Framework. Let’s take a look at its main features. We will examine a specific example that illustrates the use of this class and its methods.
Class Dictionary<K, V> – Main Operations
Creating a hash-table is done by calling some of the constructors of Dictionary<K, V>. Through them we can assign an initial value for the capacity and load factor. It’s good if we know in advance the expected number of elements, which would be added in our hash-table, so as to set it at the creation of the hash-table. This way we will avoid the unneeded expansions of the hash-table and we will achieve better performance. By default the value of the initial capacity is 16, and the load factor is 0.75.
Let’s review the methods in the class Dictionary<K, V>:
- void Add(K, V) adds a new pair (key and a value) to the hash-table. Throws an exception in the case that the key exists. This operation is extremely fast.
- bool TryGetValue(K, out V) returns an element of type V via the out parameter for the given key or null, if there is no such key. The result of this operation will be true if such an element is found. The operation is very fast, because the algorithm for searching an element by key in the hash-table is with complexity about O(1)
- bool Remove(K) removes the element with this key. This operation works very fast.
- void Clear() removes all the elements from the dictionary.
- bool ContainsKey(K) check if there is an ordered pair with this key in the dictionary. This operation works extremely fast.
- bool ContainsValue(V) checks if there is one or more ordered pairs with this value. This operation is slow because it checks every element of the hash-table (like searching in a list).
- int Count returns the number of ordered pairs within the dictionary.
- Other operations – extracting all the keys, values or ordered pairs into a structure that could be iterated through using a loop.
Students and Marks – Example
We will illustrate how to use some of the above described operations with an example. We have some students, and every one of them could have only one mark. We want to store the marks in a structure that would allow us to perform a fast search by the student’s name.
For this task we create a hash-table with initial capacity of 6. It will use the student names for keys, and their marks for values. We will add 6 sample students, and then we will check what’s happening when we print their data on the console. Here is how the code for this example should look like:
|
using System; using System.Collections.Generic; class StudentsExample { static void Main() { IDictionary<string, double> studentMarks = new Dictionary<string, double>(6);
studentMarks["Alan"] = 3.00; studentMarks["Helen"] = 4.50; studentMarks["Tom"] = 5.50; studentMarks["James"] = 3.50; studentMarks["Mary"] = 4.00; studentMarks["Nerdy"] = 6.00;
double marysMark = studentMarks["Mary"]; Console.WriteLine("Mary's mark: {0:0.00}", marysMark); studentMarks.Remove("Mary");
Console.WriteLine("Mary's mark removed.");
Console.WriteLine("Is Mary in the dictionary: {0}", studentMarks.ContainsKey("Mary") ? "Yes!": "No!");
Console.WriteLine("Nerdy's mark is {0:0.00}.", studentMarks["Nerdy"]); studentMarks["Nerdy"] = 3.25;
Console.WriteLine( "But we all know he deserves no more than {0:0.00}.", studentMarks["Nerdy"]);
double annasMark; bool findAnna = studentMarks.TryGetValue("Anna", out annasMark);
Console.WriteLine( "Is Anna's mark in the dictionary? {0}", findAnna ? "Yes!": "No!");
studentMarks["Anna"] = 6.00; findAnna = studentMarks.TryGetValue("Anna", out annasMark);
Console.WriteLine( "Let's try again: {0}. Anna's mark is {1}", findAnna ? "Yes!" : "No!", annasMark);
Console.WriteLine("Students and marks:");
foreach (KeyValuePair<string, double> studentMark in studentMarks) { Console.WriteLine("{0} has {1:0.00}", studentMark.Key, studentMark.Value); }
Console.WriteLine( "There are {0} students in the dictionary", studentMarks.Count); studentMarks.Clear(); Console.WriteLine("Students dictionary cleared."); Console.WriteLine("Is dictionary empty: {0}", studentMarks.Count == 0); } } |
The output of the program execution will be:
|
Mary's mark: 4.00 Mary's mark removed. Is Mary in the dictionary: No! Nerdy's mark is 6.00. But we all know he deserves no more than 3.25. Is Anna's mark in the dictionary? No! Let's try again: Yes!. Anna's mark is 6 Students and marks: Alan has 3.00 Helen has 4.50 Tom has 5.50 James has 3.50 Anna has 6.00 Nerdy has 3.25 There are 6 students in the dictionary Students dictionary cleared. Is dictionary empty: True |
We can see that the students are not ordered when printed. This is because in hash-tables (unlike balanced trees) the elements are not kept sorted.
Even if the current table capacity is changed while working with it, it is also highly possible that the order of the pairs could be changed as well. We will analyze the reason for this behavior later on.
It is important to remember, that with hash-tables, we cannot rely on the elements being in order. If we need them ordered, we could sort the elements before printing. Another option would be using SortedDictionary<K, V>.
Hashing and Hash-Functions
Now we will explain in more details the concept of hash-code used earlier. The hash-code is a number returned by the hash-function, used for the hashing the key. This number should be different for every key, or at least there should be a high chance for that.
Hash-Functions
There is the concept of the perfect hash-function. One hash-function is called perfect, if for example you have N keys, and for each of them the function would add a different number in a reasonable interval (for example from 0 to N-1).
Finding such a function in the common case is a very hard, almost impossible task. It’s worth to use such functions when using sets of keys with predefined elements or when the set of keys is rarely changed.
In practice there are also other, not so "perfect" hash-functions.
Now we will take a look at a few examples for hash-functions, which are used directly with .NET libraries.
The Method GetHashCode() in .NET Framework
Every .NET class has a method called GetHashCode() that returns a value of type int. This method is inherited by the class Object, which is the root member in the hierarchy of .NET classes.
The implementation in the class Object of the method GetHashCode() does not guarantee the unique value of the result. This means that the descendent classes need to ensure that GetHashCode() is implemented in order to use it for a key in a hash-table.
Another example for a hash-function that is directly built in .NET is used by the class int, byte and short (integer numbers). In this case the value of the number itself is used for the hash-code. For more complex types like strings all their elements (or at least the first few of them) are involved into calculation of their hash code.
One more complex example for hash-function is the implementation of GetHashCode() in the class System.String:
|
public override unsafe int GetHashCode() { fixed (char* str = ((char*)this)) { char* chPtr = str; int num = 352654597; int num2 = num; int* numPtr = (int*)chPtr; for (int i = this.Length; i > 0; i -= 4) { num = (((num << 5) + num) + (num >> 27)) ^ numPtr[0]; if (i <= 2) { break; } num2 = (((num2 << 5) + num2) + (num2 >> 27)) ^ numPtr[1]; numPtr += 2; } return (num + (num2 * 1566083941)); } } |
This implementation is complicated, but what we need to remember is that it tries to guarantee the uniqueness of the result: different hash code for different input strings. Note that the complexity of the algorithm for calculating the hash-code of string is proportional to Length / 4 or O(n), which means that the longer the string is the slower its hash-code would be calculated. Authors of the above code use a small trick (unsafe code) to directly work with the low-level representation of the string in the memory.
We leave to the reader to take a look at other implementations of the method GetHashCode() in some of the most commonly used .NET types like int, DateTime, long, float and double. This can be done through a decompiler like JustDecompile.
Now let’s answer the question of how to implement ourselves this hash function for our classes. We already explained that leaving the implementation that is already built in the class object, is not an acceptable solution. Another very simple implementation is that we always return a fixed constant, for example:
|
public override int GetHashCode() { return 42; } |
If in a hash-table we use objects for keys from a class, that has the above implementation of GetHashCode(), it will have very poor performance, because every time, when we add a new element in the table, we would have to insert it at the same place. Every time we search the hash-table, we will encounter the same element.
In order to avoid the described behavior, we need the hash-function to distribute the keys evenly amongst the possible hash-code values.
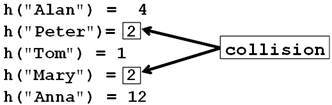
Collisions with Hash-Functions
The situation where two different keys have the same hash-code is called collision. A good example of collision is shown below:
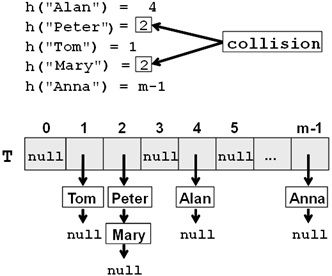
We will look in more details how to solve the problem with collisions in the next paragraph. The simplest solution is obvious: order the pairs that have keys with the same hash-codes in a list or other data structure. Thus we don't solve the collisions but we accept them and we just put several key-value-pairs in the same element in the underlying array in the hash-table. This approach for collision resolution is known as chaining:
Therefore when using a constant 42 for hash-code our hash-table turns into a linear list and it becomes very inefficient.
Implementing the Method GetHashCode()
We will give a standard algorithm for implementing GetHashCode(), when this is necessarily:
First we need to choose which fields of the class will take part in the implementation of the Equals(object) method. This is necessary, because every time when Equals() returns true, the result from GetHashCode() should always return the same value.
This way the fields that do not take part in Equals(), should not take part in GetHashCode() as well.
After we choose which fields will take part for the calculation of GetHashCode(), we need to receive values from them (of type int). Here is a sample scheme:
- If the field is bool, for true we take 1, and for false we take 0 (or directly call method GetHashCode() on bool).
- If the field is of type int, byte, short, char, we can convert it to int, with the cast operator (int) (or we could directly call GetHashCode()).
- If the field is type long, float or double, we could use the result from their own implementations of GetHashCode().
- If the field is not a primitive type, we could call the method GetHashCode() of this object. If the field value is null, we can return 0.
- If the field is an array or a collection, we take the hash-code from every element of this collection.
In the end we sum all the received int values, and before each addition we multiply the temporary result with a prime number (for example 83), while ignoring the eventual overflow of type int. For example, if we have 3 fields and their hash codes are f1, f2 and f3, our hash function could combine them though the formula hash = (((f1 * 83) + f2) * 83) + f3.
At the end we obtain a hash-code, which is very well distributed in the range of all 32-bit values. We can expect, that with a hash-code calculated this way, the collisions would be rare, because every change in some of the fields taking part in GetHashCode() leads to a major change in the hash code and thus reduces the chance for collision.
Implementing GetHashCode() – Example
Let’s illustrate the above algorithm with an example. We have a class whose objects are presented as points in the three-dimensional space. The point will be represented with its coordinates in the three dimensional space x, y and z:
|
Point3D.cs |
|
public class Point3D { public double X { get; set; } public double Y { get; set; } public double Z { get; set; }
public Point3D(double x, double y, double z) { this.X = x; this.Y = y; this.Z = z; }
public override string ToString() { return String.Format("({0}, {1}, {2})", this.X, this.Y, this.Z); } } |
We can implement GetHashCode() easily using the above described algorithm that combines the hash values of the separate object fields:
|
public override bool Equals(object obj) { if (this == obj) return true;
Point3D other = obj as Point3D;
if (other == null) return false;
if (!this.X.Equals(other.X)) return false;
if (!this.Y.Equals(other.Y)) return false;
if (!this.Z.Equals(other.Z)) return false;
return true; }
public override int GetHashCode() { int prime = 83; int result = 1; unchecked { result = result * prime + X.GetHashCode(); result = result * prime + Y.GetHashCode(); result = result * prime + Z.GetHashCode(); }
return result; } |
This implementation is incomparably better, than returning a constant or just one of the fields or their sum. Although the collisions might still happen, they would occur very rarely.
Interface IEqualityComparer<T>
One of the most important things that we have learned so far is that in order to use instances of a class as keys for a dictionary, the class needs to properly implement GetHashCode() and Equals(…). But what should we do if we want to use a class, that we cannot inherit or change? In this case the interface IEqualityComparer<T> comes to our aid.
It defines the following two operations:
- bool Equals(T obj1, T obj2) – returns true if obj1 and obj2 are equal
- int GetHashCode(T obj) – returns the hash-code of given object
As you might have already guessed, the dictionaries in .NET can use an instance of IEqualityComparer<T>, instead of using the corresponding methods of the given class that should be assigned for a key. This way the developers could use practically any class for a key of the dictionary, if they could assure IEqualityComparer<T> is implemented. Even more – when we pass IEqualityComparer<T> to a dictionary, we could change the way GetHashCode() and Equals(…) are calculated for every type, even for those built-in .NET Framework. This is because the dictionary uses interface methods instead of the corresponding methods of the class that is used for key. Here is an example of an implementation of IEqualityComparer for the class Point3D that we looked earlier:
|
public class Point3DEqualityComparer : IEqualityComparer<Point3D> { public bool Equals(Point3D point1, Point3D point2) { if (point1 == point2) return true;
if (point1 == null || point2 == null) return false;
if (!point1.X.Equals(point2.X)) return false;
if (!point1.Y.Equals(point2.Y)) return false;
if (!point1.Z.Equals(point2.Z)) return false;
return true; }
public int GetHashCode(Point3D obj) { Point3D point = obj as Point3D; if (point == null) { return 0; }
int prime = 83; int result = 1; unchecked { result = result * prime + point.X.GetHashCode(); result = result * prime + point.Y.GetHashCode(); result = result * prime + point.Z.GetHashCode(); } return result; } } |
Note that we implement both Equals(…) and GetHashCode(), not just GetHashCode() method.
|
Remember that the keys in hash-tables need to have correctly defined Equals(…) and GetHashCode() to work properly. This is not required for the values, just for the keys. Always define both Equals(…) and GetHashCode(), never only one of them! |
In order to use Point3DEqualityComparer, it’s enough to pass it as argument to our dictionary’s constructor. Here is an example:
|
static void Main() { IEqualityComparer<Point3D> comparer = new Point3DEqualityComparer(); Dictionary<Point3D, int> dict = new Dictionary<Point3D, int>(comparer);
dict[new Point3D(4, 2, 5)] = 5; dict[new Point3D(1, 2, 3)] = 1; dict[new Point3D(3, 1, -1)] = 3; dict[new Point3D(1, 2, 3)] = 10; foreach (var entry in dict) { Console.WriteLine("{0} --> {1}", entry.Key, entry.Value); } } |
The result from the above code is:
|
(4, 2, 5) --> 5 (1, 2, 3) --> 10 (3, 1, -1) --> 3 |
We have 3 unique keys in the dictionary and the key (1, 2, 3) is used twice.
Resolving the Collision Problem
In practice, collisions happen almost always, excluding some rare and specific cases. That is why we need to live with the idea of the collisions presence in our hash-tables and take them into account. Let’s have a look at several strategies for dealing with collisions.
Chaining in a List
The most widespread method to resolve collisions problem is called chaining. Its major concept consists of storing in a list all the pairs (key, value), which have the same hash-code for the key.
Implementation of a Dictionary with Hash-Table and Chaining
Let’s have the task to implement a dictionary data structure with a hash-table and to resolve the collisions by chaining. With the example below we will show how it could be done. First, we are going to define a class, describing the pair {key, value}:
|
KeyValuePair.cs |
|
/// <summary>A structure holding a pair {key, value}</summary> /// <typeparam name="TKey">the type of the keys</typeparam> /// <typeparam name="TValue">the type of the values</typeparam> public struct KeyValuePair<TKey, TValue> { /// <summary>Holds the key of the key-value pair</summary> public TKey Key { get; private set; }
/// <summary>Holds the value of the key-value pair</summary> public TValue Value { get; private set; }
/// <summary>Constructs a pair by given key + value</summary> public KeyValuePair(TKey key, TValue value) : this() { this.Key = key; this.Value = value; }
/// <summary>Converts the key-value pair to a printable text. /// </summary> public override string ToString() { StringBuilder builder = new StringBuilder(); builder.Append('['); if (this.Key != null) { builder.Append(this.Key.ToString()); } builder.Append(", "); if (this.Value != null) { builder.Append(this.Value.ToString()); } builder.Append(']'); return builder.ToString(); } } |
The class constructor has two parameters: key of type TKey and value of type TValue. There are defined two properties: one to access the key (Key) and another to access the value (Value). Note that these properties can only access the related members. There is no public functionality to change the key or value. This makes the class non-changeable (immutable). It is a good idea, because the objects, which will be kept inside the dictionary implementation, will be the same as these we will return as a result of a method for taking all the ordered pairs in the dictionary, for instance.
We have redefined the ToString() method in order to be able to easily print key-value pairs on the standard console output or in a text file.
Following is an example of a generic dictionary interface, which defines the most common operations of the data structure "dictionary":
|
IDictionary.cs |
|
/// <summary>Interface that defines basic methods needed for a /// "dictionary" class which maps keys to values</summary> /// <typeparam name="K">Key type</typeparam> /// <typeparam name="V">Value type</typeparam> public interface IDictionary<K, V> : IEnumerable<KeyValuePair<K, V>> { ///<summary>Finds the value mapped to the given key</summary> /// <param name="key">the key to be searched</param> /// <returns>value for the specified key if it presents, /// or null if there is no value with such key</returns> V Get(K key);
/// <summary>Assigns the specified value to the specified key /// in the dictionary. If the key already exists, its value is /// replaced with the new value and the old value is returned /// </summary> /// <param name="key">Key for the new value</param> /// <param name="value">Value to be mapped to that key</param> /// <returns>the old (replaced) value for the specified key /// or null if the key does not exist</returns> V Set(K key, V value);
/// <summary>Gets or sets the value of the entry in the /// dictionary identified by the key specified</summary> /// <remarks>A new entry will be created if the value is set /// for a key not currently in the dictionary</remarks> /// <param name="key">the key to identify the entry</param> /// <returns>the value of the entry in the dictionary /// identified by the provided key</returns> V this[K key] { get; set; }
/// <summary>Removes an element in the dictionary identified /// by a specified key</summary> /// <param name="key">the key identifying the element to be /// removed</param> /// <returns>whether the element was removed or not</returns> bool Remove(K key);
/// <summary>Returns the number of entries in the dictionary /// </summary> int Count { get; }
/// <summary>Removes all the elements from the dictionary /// </summary> void Clear(); } |
In the above defined interface as well as in the previous class, we use generics (template types), by which we define the parameters for the keys (K) and values (V). Such implementation allows us to use various data types for keys and values inside our dictionary. As we already know, the only requirement is to have proper definitions for Equals() and GetHashCode() methods inside the data type used for the keys.
Our interface IDictionary<K, V> looks much like the .NET standard interface System.Collections.Generic.IDictionary<K, V>, but it is simplified and describes only the most important operations of the "dictionary" data structure. It inherits the system interface IEnumerable<DictionaryEntry<K, V>>, as doing so, the dictionary can be easily traversed by a simple foreach loop.
Following is an example of a dictionary implementation that uses chaining to handle collisions.
|
HashDictionary.cs |
|
/// <summary> /// Implementation of <see cref="IDictionary"/> interface /// using a hash table. Collisions are resolved by chaining. /// </summary> /// <typeparam name="K">Type of the keys. Keys are required /// to correctly implement Equals() and GetHashCode() /// </typeparam> /// <typeparam name="V">Type of the values</typeparam> public class HashDictionary<K, V> : IDictionary<K, V>, IEnumerable<KeyValuePair<K, V>> { private const int DEFAULT_CAPACITY = 16; private const float DEFAULT_LOAD_FACTOR = 0.75f; private List<KeyValuePair<K, V>>[] table; private float loadFactor; private int threshold; private int size; private int initialCapacity;
/// <summary>Creates an empty hash table with the /// default capacity and load factor</summary> public HashDictionary() : this(DEFAULT_CAPACITY, DEFAULT_LOAD_FACTOR) { }
/// <summary>Creates an empty hash table with given /// capacity and load factor</summary> public HashDictionary(int capacity, float loadFactor) { this.initialCapacity = capacity; this.table = new List<KeyValuePair<K, V>>[capacity]; this.loadFactor = loadFactor; this.threshold = (int)(capacity * this.loadFactor); }
/// <summary>Finds the chain of elements corresponding /// internally to given key (by its hash code)</summary> /// <param name="createIfMissing">creates an empty list /// of elements if the chain still does not exist</param> /// <returns>a list of elements in the chain or null</returns> private List<KeyValuePair<K, V>> FindChain( K key, bool createIfMissing) { int index = key.GetHashCode(); index = index & 0x7FFFFFFF; // clear the negative bit index = index % this.table.Length; if (this.table[index] == null && createIfMissing) { this.table[index] = new List<KeyValuePair<K, V>>(); } return this.table[index] as List<KeyValuePair<K, V>>; }
/// <summary>Finds the value assigned to given key /// (works extremely fast)</summary> /// <returns>the value found or null when not found</returns> public V Get(K key) { List<KeyValuePair<K, V>> chain = this.FindChain(key, false); if (chain != null) { foreach (KeyValuePair<K, V> entry in chain) { if (entry.Key.Equals(key)) { return entry.Value; } } }
return default(V); }
/// <summary>Assigns a value to certain key. If the key /// exists, its value is replaced. If the key does not /// exist, it is first created. Works very fast</summary> /// <returns>the old (replaced) value or null</returns> public V Set(K key, V value) { if (this.size >= this.threshold) { this.Expand(); }
List<KeyValuePair<K, V>> chain = this.FindChain(key, true); for (int i = 0; i < chain.Count; i++) { KeyValuePair<K, V> entry = chain[i]; if (entry.Key.Equals(key)) { // Key found -> replace its value with the new value KeyValuePair<K, V> newEntry = new KeyValuePair<K, V>(key, value); chain[i] = newEntry; return entry.Value; } } chain.Add(new KeyValuePair<K, V>(key, value)); this.size++;
return default(V); }
/// <summary>Gets / sets the value by given key. Get returns /// null when the key is not found. Set replaces the existing /// value or creates a new key-value pair if the key does not /// exist. Works very fast</summary> public V this[K key] { get { return this.Get(key); } set { this.Set(key, value); } }
/// <summary>Removes a key-value pair specified /// by certain key from the hash table.</summary> /// <returns>true if the pair was found removed /// or false if the key was not found</returns> public bool Remove(K key) { List<KeyValuePair<K, V>> chain = this.FindChain(key, false);
if (chain != null) { for (int i = 0; i < chain.Count; i++) { KeyValuePair<K, V> entry = chain[i]; if (entry.Key.Equals(key)) { // Key found -> remove it chain.RemoveAt(i); this.size--; return true; } } } return false; }
/// <summary>Returns the number of key-value pairs /// in the hash table (its size)</summary> public int Count { get { return this.size; } }
/// <summary>Clears all ements of the hash table</summary> public void Clear() { this.table = new List<KeyValuePair<K, V>>[this.initialCapacity]; this.size = 0; }
/// <summary>Expands the underlying hash-table. Creates 2 /// times bigger table and transfers the old elements /// into it. This is a slow (linear) operation</summary> private void Expand() { int newCapacity = 2 * this.table.Length; List<KeyValuePair<K, V>>[] oldTable = this.table; this.table = new List<KeyValuePair<K, V>>[newCapacity]; this.threshold = (int)(newCapacity * this.loadFactor); foreach (List<KeyValuePair<K, V>> oldChain in oldTable) { if (oldChain != null) { foreach (KeyValuePair<K, V> keyValuePair in oldChain) { List<KeyValuePair<K, V>> chain = FindChain(keyValuePair.Key, true); chain.Add(keyValuePair); } } } }
/// <summary>Implements the IEnumerable<KeyValuePair<K, V>> /// to allow iterating over the key-value pairs in the hash /// table in foreach-loops</summary> IEnumerator<KeyValuePair<K, V>> IEnumerable<KeyValuePair<K, V>>.GetEnumerator() { foreach (List<KeyValuePair<K, V>> chain in this.table) { if (chain != null) { foreach (KeyValuePair<K, V> entry in chain) { yield return entry; } } } }
/// <summary>Implements IEnumerable (non-generic) /// as part of IEnumerable<KeyValuePair<K, V>></summary> IEnumerator IEnumerable.GetEnumerator() { return ((IEnumerable<KeyValuePair<K, V>>)this). GetEnumerator(); } } |
We will pay attention to the most important points in this code. Let’s begin with the constructor. The public parameterless constructor inside itself it invokes another constructor, by passing some predefined values for capacity and load factor, which are used when the hash table is created.
Next thing, we pay attention to, is the actual implementation of the hash table with chaining. At the instantiation of the hash-table, inside the constructor we initialize an array of lists, which will contain any of our objects of type KeyValuePair<K,V>. We have created a private method FindChain(), for internal usage only, which calculates the hash-code of the key by calling GetHashCode() method and taking the modulus of the returned hash-value to the length of the table (capacity). Additionally the most-left bit is cleared to ensure the index is always a positive number. In that way the index of the current key in the internal table is calculated. The list of all the elements with the same hash-code is hold inside the internal table for this index. If the list is empty, it may have null as a value. Otherwise, at the specific index position there is a list of the elements for the specified key.
A special parameter is passed to the FindChain() method. This parameter indicates whether to create an empty list, if for the specific key there is no list of elements. It gives a kind of convenience for the methods of adding elements and resizing the hash-table.
The next thing, we pay attention to, is the Expand() method, which resizes the current internal table when the maximal allowed filling is reached. For this purpose we create a new table (array), with size twice as the current. Then we calculate a new value for the maximal allowed filling (the field threshold). Next coming is the most important part. We have extended the table and in this way we changed the value of this.table.Length. If we search for an element, which we have added already, the FindChain(K key) method will not return the correct chain at all, in which to search for it. That is why, we need to transfer all the elements of the old table, by not just copying the chains, but adding again all the KeyValuePair<K,V> objects into the newly created internal table of chains.
In order to implement the ability for iteration over the hash-table elements in foreach-loops, we have implemented the IEnumerable<KeyValuePair<K, V>> interface, which has GetEnumerator() method, returning an iterator (IEnumerator) of the elements of the hash-table. We simply iterate over the elements in the internal table and return them one at a time using the yield return C# keyword (it’s is a complex concept explained in details in MSDN).
Now let’s give an example of how we can use our implementation of hash-table and its iterator. We want to test whether the hash table copes correctly with collisions and with expanding, so we intentionally change the initial capacity of 3 and load factor of 0.9 when creating the hash table to ensure it will resize soon after few elements are put inside it. We first put an element, then read it, then overwrite its value, then read it again, then add a new element that causes a collision, then read it, then read the first element, then add an element causing the hash table to expand its internal array, etc. The code is given below and it is highly recommended to trace it through the Visual Studio debugger and check at each step how the internal state of the hash table changes:
|
class PlayWithHashDictionary { static void Main() { HashDictionary<Point3D, int> dict = new HashDictionary<Point3D, int>(3, 0.9f);
dict[new Point3D(1, 2, 3)] = 1; // Put a key-value pair Console.WriteLine(dict[new Point3D(1, 2, 3)]); // Get value
// Overwrite the previous value for the same key dict[new Point3D(1, 2, 3)] += 1; Console.WriteLine(dict[new Point3D(1, 2, 3)]);
// Now this point will cause a collision with the // previous one and the elements will be chained dict[new Point3D(3, 2, 2)] = 42;
Console.WriteLine(dict[new Point3D(3, 2, 2)]);
// Test if the chaining works as expected, i.e. // elements with equal hash-codes are not overwritten Console.WriteLine(dict[new Point3D(1, 2, 3)]);
// Creation of another entry in the internal table // This will cause the internal table to expand dict[new Point3D(4, 5, 6)] = 1111; Console.WriteLine(dict[new Point3D(4, 5, 6)]);
// Delete an existing by its key dict.Remove(new Point3D(3, 2, 2));
// Iterate through the dictionary entries and print them foreach (KeyValuePair<Point3D, int> entry in dict) { Console.WriteLine( "Key: " + entry.Key + "; Value: " + entry.Value); } } } |
As we could expect, the result of the program execution is the following:
|
1 2 42 2 1111 Key: (1, 2, 3); Value: 2 Key: (4, 5, 6); Value: 1111 |
Open Addressing Methods for Collision Resolution
Now let’s look over the methods for collision resolution, alternative to chaining in a list. In general, the idea is, in case of collision we try to put the new pair in a table position, which is free. These methods differentiate from each other in the way they choose where to look for a free position for the new pair. Moreover, the new pair must be easily located at its new place.
Main drawback of this group of methods, compared to chaining in a list, is that they are inefficient at high rates of the load factor (close to 1).
Linear Probing
This is one of easiest methods for implementation. Linear probing, in general, can be presented with the following sample code:
|
int newPosition = (oldPosition + i) % capacity; |
Here capacity is the internal table capacity, oldPostion is the position where collision occurs and i is a number for the next probing. If the new position is free, then we place the new pair there. Otherwise we try again (probing), incrementing i. Probing can be either forward or backwards. Backward probing is when instead of adding, we are subtracting i from the position we have collision for.
The advantage of this method is the relatively quick way to find of a new position. Unfortunately, if there was a collision at a certain place, there is an extremely high probability collision to occur again at the same place. So this, in practice, leads to a high inefficiency.
|
Using linear probing as a method for collision resolution in hash tables is inefficient and has to be avoided. |
Quadratic Probing
Quadratic probing is a classic method for collision resolution. The main difference between quadratic probing and linear probing is that it uses a quadratic function of i (the number of the next probing) to find new position. Possible quadratic probing function is shown below:
|
int newPosition = (oldPosition + c1*i + c2*i*i) % capacity; |
The given example uses two constants: c1 and c2, such that c2 must not be 0, otherwise we are going back to linear probing.
By choosing c1 and c2 we define the position we are going to probe, compared to the starting position. For instance, if c1 and c2 are equal to 1, we are going to probe consequently oldPosition, oldPosition + 2, oldPosition + 6, … For a hash-table with capacity of the kind 2n, the best is to choose c1 and c2 equal to 0.5.
Quadratic probing is more efficient than linear the linear probing.
Double Hashing
As the name implies, the double hashing method uses two different hash functions. The main concept is that, the second hash function is used for the elements that fall into a collision. This method is better than the linear and quadratic probing, because all the next probing depends of the value of the key and not of the table position inside the hash-table. It makes sense, because the position of a given key depends on the current capacity of the hash-table.
Cuckoo Hashing
Cuckoo hashing is a relatively new method for collision resolution, using an open addressing. It was firstly presented by R. Pagh and F. Rodler in 2001. Its name comes from the behavior, observed with some kinds of cuckoos. The mother cuckoos push out the eggs and/or the nests out of other birds, in order to put their own eggs there and the other birds mistakenly care for the cuckoos' eggs in that way. (Also for the nests, after the incubation)
The main idea of this method is the use of two hash-functions instead of one. In this way, we have not one, but two positions to place the element inside the hash-table. If one of the positions is free, then we just put the element there. If both are taken, then we put the new element in one of them and it "kicks out" the element, which was already there. In turn, the "kicked" element is going to his alternative position and "kicks" another element out, if necessary. The new "kicked out" is repeating the procedure, and in that way until reaching a free position or we fall into a loop. In the last case, the whole hash table is built again with greater size and new hash-functions.
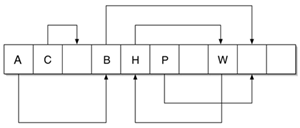
On the figure bellow it is shown an example scheme of a hash-table using cuckoo hashing. Every position, containing an element, has a link to the alternative position for the key inside. Now, let’s play out different situations of adding an element.
If, at least one of the two hash functions result is a free cell, there is no problem. We put the element in one of them. Let both hash functions result is a taken cell and we randomly have been choosing one of them.
Let’s assume that this is the cell, containing element A. The new element "kicks out" A from his place, A in turn goes to its alternative position and "kicks out" B from his place. The alternative position of B is free, so the adding is successfully completed.
Let’s assume, that the cell, the new element is trying to "kick out" an element, is the cell containing H. Then we have a loop, formed by H and W. In this case, a rebuild must be done using greater size, and new hash-functions.
In its simplest version this method has a constant access to its elements, even in the worst case, but this is valid with the constraint that the load factor is less than 0.5.
The use of three different hash-functions instead of two could result in an efficient upper limit of the load factor above 0.9.
Some researches show, the cuckoo hashing and its modifications could be much more efficient than the widely spread today chaining in a list and open addressing methods. Nevertheless, this method is still not well adopted in the industry and not used internally in .NET Framework. The main stopper is the need of two hash functions, which means that the class System.Object should introduce two GetHashCode() methods.
In this section we will look over the abstract data structure "set" and two of its typical implementations. We will explain their advantages and disadvantages and which of them should be preferred for different situations.
The Abstract Data Structure "Set"
Sets are collections of unique elements (without any repeating elements inside). In the .NET context, it means, for every set object, calling its Equals() method and passing another object from the set as an argument, will always result in false. Note that two different objects in .NET may be equal when compared by certain field and thus in the data structure "set" only one of them could be put.
Some sets allow their elements to be null, while others do not allow.
Besides not allowing the repetition of objects, another important thing, that distinguishes sets from lists and arrays, is that the set element has no index. The elements of the set cannot be accessed by any key, as it is with dictionaries. The elements themselves are the keys.
The only way to access an object from a set is by having available either the object itself or another object, which is equal to it. That is why, in practice we access all the elements of a given set at once, while iterating, by using the foreach loop construct.
Set Implementations in .NET Framework
In .NET (version 4.0 and above) there is an interface ISet<T> representing the ADT "set" and it has two standard implementation classes:
- HashSet<T> – hash-table based implementation of set.
- SortedSet<T> – red-black tree based implementation of set.
Let’s review both of them and see their strong and weak sides.
The main operations, defined by the ISet<T> interface (abstract data structure set), are the following:
- bool Add(element) – adding the element to the set and returning false if the element is already present inside the set, otherwise returning true.
- bool Contains(element) – checks if the set already contains the element passed as an argument. If yes, returns true as a result, otherwise returns false.
- bool Remove(element) – removes the element from the set. Returns Boolean if the element has been present inside the set.
- void Clear() – removes all the elements from the set.
- void IntersectWith(Set other) – inside the current set remain only the elements of the intersection of both sets – the result is a set, containing the elements, which are present in both sets at the same time – the set, calling the method and the other, passed as parameter.
- void UnionWith(Set other) – inside the current set remain only the elements of the sets union – the result is a set, containing the elements of either one or the other, or both sets.
- bool IsSubsetOf(Set other) – checks if the current set is a subset of the other set. Returns true, if yes and false, if no.
- bool IsSupersetOf(Set other) – checks if the other set is a subset of the current one. Returns true, if yes and false, if no.
- int Count – a property, which returns the current number of elements inside the set.
Implementation with Hash-Table – HashSet<T>
As we already mentioned, the hash-table implementation of set in .NET is the HashSet<T> class. This class, like Dictionary<K, V>, has constructors, by which we might pass a list of elements, as well as an IEqualityComparer implementation, mentioned earlier. They have the same semantics, because here we use a hash-table again.
Here is an example, which demonstrates the use of sets and the already described, operations: union and intersection:
|
using System; using System.Collections.Generic;
class StudentListSetsExample { static void Main() { HashSet<string> aspNetStudents = new HashSet<string>(); aspNetStudents.Add("S. Jobs"); aspNetStudents.Add("B. Gates"); aspNetStudents.Add("M. Dell");
HashSet<string> silverlightStudents = new HashSet<string>(); silverlightStudents.Add("M. Zuckerberg"); silverlightStudents.Add("M. Dell");
HashSet<string> allStudents = new HashSet<string>(); allStudents.UnionWith(aspNetStudents); allStudents.UnionWith(silverlightStudents);
HashSet<string> intersectStudents = new HashSet<string>(aspNetStudents); intersectStudents.IntersectWith(silverlightStudents);
Console.WriteLine("ASP.NET students: " + string.Join(", ", aspNetStudents)); Console.WriteLine("Silverlight students: " + string.Join(", ", silverlightStudents)); Console.WriteLine("All students: " + string.Join(", ", allStudents)); Console.WriteLine( "Students in both ASP.NET and Silverlight: " + string.Join(", ", intersectStudents)); } } |
And the output from the above code is:
|
ASP.NET students: S. Jobs, B. Gates, M. Dell Silverlight students: M. Zuckerberg, M. Dell All students: S. Jobs, B. Gates, M. Dell, M. Zuckerberg Students in both ASP.NET and Silverlight: M. Dell |
Pay attention that "M. Dell" is present in both sets, but inside the union it is present only once. That is, because, as we already explained, one element might be present at most once in a given set.
Implementation with Red-Black Tree – SortedSet<T>
The standard .NET class SortedSet<T> is a set, implemented by a balanced search tree (red-black tree). Because of this, its elements are internally kept in an increasing order. For that reason we can only add elements, which are comparable. We remind that in .NET it typically means the objects are instances of a class, implementing IComparable<T>. We would demonstrate the use of the SortedSet<T> class by the following example:
|
using System; using System.Collections.Generic;
class SortedSetsExample { static void Main() { SortedSet<string> bandsBradLikes = new SortedSet<string>(new[] { "Manowar", "Blind Guardian", "Dio", "Kiss", "Dream Theater", "Megadeth", "Judas Priest", "Kreator", "Iron Maiden", "Accept" });
SortedSet<string> bandsAngelinaLikes = new SortedSet<string>(new[] { "Iron Maiden", "Dio", "Accept", "Manowar", "Slayer", "Megadeth", "Running Wild", "Grave Gigger", "Metallica" });
Console.Write("Brad Pitt likes these bands: "); Console.WriteLine(string.Join(", ", bandsBradLikes));
Console.Write("Angelina Jolie likes these bands: "); Console.WriteLine(string.Join(", ", bandsAngelinaLikes));
SortedSet<string> intersectBands = new SortedSet<string>(bandsBradLikes); intersectBands.IntersectWith(bandsAngelinaLikes);
Console.WriteLine(string.Format( "Does Brad Pitt like Angelina Jolie? {0}", intersectBands.Count >= 5 ? "Yes!" : "No!"));
Console.Write( "Because Brad Pitt and Angelina Jolie both like: "); Console.WriteLine(string.Join(", ", intersectBands));
SortedSet<string> unionBands = new SortedSet<string>(bandsBradLikes); unionBands.UnionWith(bandsAngelinaLikes);
Console.Write( "All bands that Brad Pitt or Angelina Jolie like: "); Console.WriteLine(string.Join(", ", unionBands)); } } |
And the output of the program execution is:
|
Brad Pitt likes these bands: Accept, Blind Guardian, Dio, Dream Theater, Iron Maiden, Judas Priest, Kiss, Kreator, Manowar, Megadeth Angelina Jolie likes these bands: Accept, Dio, Grave Gigger, Iron Maiden, Manowar, Megadeth, Metallica, Running Wild, Slayer Does Brad Pitt like Angelina Jolie? Yes! Because Brad Pitt and Angelina Jolie both like: Accept, Dio, Iron Maiden, Manowar, Megadeth All bands that Brad Pitt or Angelina Jolie like: Accept, Blind Guardian, Dio, Dream Theater, Grave Gigger, Iron Maiden, Judas Priest, Kiss, Kreator, Manowar, Megadeth, Metallica, Running Wild, Slayer |
As we may note, the elements in all set are always ordered, in comparison with HashSet<T>.
1. Write a program that counts, in a given array of integers, the number of occurrences of each integer.
Example: array = {3, 4, 4, 2, 3, 3, 4, 3, 2}
2 à 2 times 3 à 4 times 4 à 3 times
2. Write a program to remove from a sequence all the integers, which appear odd number of times. For instance, for the sequence {4, 2, 2, 5, 2, 3, 2, 3, 1, 5, 2, 6, 6, 6} the output would be {5, 3, 3, 5}.
3. Write a program that counts how many times each word from a given text file words.txt appears in it. The result words should be ordered by their number of occurrences in the text.
Example: "This is the TEXT. Text, text, text – THIS TEXT! Is this the text?"
Result: is à 2, the à 2, this à 3, text à 6.
4. Implement a DictHashSet<T> class, based on HashDictionary<K, V> class, we discussed in the text above.
5. Implement a hash-table, maintaining triples (key1, key2, value) and allowing quick search by the pair of keys and adding of triples.
6. Implement a hash-table, allowing the maintenance of more than one value for a specific key.
7. Implement a hash-table, using "cuckoo hashing" with 3 hash-functions.
8. Implement the data structure hash-table in a class HashTable<K,T>. Keep the data in an array of key-value pairs (KeyValuePair<K,T>[]) with initial capacity of 16. Resole the collisions with quadratic probing. When the hash table load runs over 75%, perform resizing to 2 times larger capacity. Implement the following methods and properties: Add(key, value), Find(key) à value, Remove(key), Count, Clear(), this[] and Keys. Try to make the hash-table to support iterating over its elements with foreach.
9. Implement the data structure "Set" in a class HashedSet<T>, using your class HashTable<K, T> to hold the elements. Implement all standard set operations like Add(T), Find(T), Remove(T), Count, Clear(), union and intersect.
10. We are given three sequences of numbers, defined by the formulas:
- f1(0) = 1; f1(k) = 2*f1(k-1) + 3; f1 = {1, 5, 13, 29, …}
- f2(0) = 2; f2(k) = 3*f2(k-1) + 1; f2 = {2, 7, 22, 67, …}
- f3(0) = 2; f3(k) = 2*f3(k-1) - 1; f3 = {2, 3, 5, 9, …}
Write a program to find the intersection and union of sets of sequences’ elements within the range [0; 100000]: f1 * f2; f1 * f3; f2 * f3; f1 * f2 * f3; f1 + f2; f1 + f3; f2 + f3; f1 + f2 + f3. Here + and * mean respectively union and intersection of sets.
11. * Define TreeMultiSet<T> class, which allows to keep a set of elements, in increasing order and to have duplicates of the elements. Implement operations adding of element, finding the number of occurrences, deletion, iterator, min / max element finding, min / max deletion. Implement the possibility to pass an external Comparer<T> for elements comparison.
12. * We are given a list of arriving and departing schedule at a bus station. Write a program, using the HashSet<T> class, which by given interval (start, end) returns the number of buses, which have arrived and departed during that time.
Example:
We have the data of the following buses: [08:24-08:33], [08:20-09:00], [08:32-08:37], [09:00-09:15]. We are given the range [08:22-09:05]. The number of buses, arriving and departing during that time is 2.
13. * We are given a sequence P containing L integers L (1 < L < 50,000) and a number N. We call a “lucky sub-sequence within P” every sub-sequence of integers from P with a sum equal to N.
Imagine we have a sequence S, holding all the lucky sub-sequences of P, kept in decreasing order by their length. When the length is the same, the sequences are ordered in decreasing order by their elements: from the leftmost to the rightmost. Write a program to return the first 10 elements of S.
Example: We are given N = 5 and the sequence P = {1, 1, 2, 1, -1, 2, 3, -1, 1, 2, 3, 5, 1, -1, 2, 3}. The sequence S consists of the following 13 sub-sequences of P:
- [1, -1, 2, 3, -1, 1]
- [1, 2, 1, -1, 2]
- [3, -1, 1, 2]
- [2, 3, -1, 1]
- [1, 1, 2, 1]
- [1, -1, 2, 3]
- [1, -1, 2, 3]
- [-1, 1, 2, 3]
- [5, 1, -1]
- [2, 3]
- [2, 3]
- [2, 3]
- [5]
The last 10 elements of P are given in bold.
1. Use Dictionary<TKey, TValue> counts and though a single scan through the input numbers count the occurrences of each one. When you pass through a number p, if it is missing in the dictionary counts[p] = 1. If the number is already stored in the dictionary, increase its count: counts[p] = counts[p] + 1. Finally scan through the element of the dictionary (with foreach-loop) and print its key-value pairs.
2. Use Dictionary<K, T> to count how many times each element occurs (like in the previous problem) and List<T> where you can add all elements occurring even number of times.
3. Use Dictionary<string, int> with word as a key and number of occurrences as a value. After counting all the words, sort the dictionary by value using something like this:
|
var sorted = dictionary.OrderBy(p => p.Value); |
To use the OrderBy(<keySelector>) extension method you need to include the System.Linq namespace.
4. Use the element of the set as key and value at the same time.
5. Use hash-table of hash-tables: Dictionary<key, Dictionary<key, value>>. Think about how to add and search elements in this structure.
6. Use Dictionary<K, List<V>>.
7. You can use GetHashCode() % size as the first hash-function, (GetHashCode() * 83 + 7) % size as the second, (GetHashCode () * GetHashCode() + 19) % size) as the third.
8. Follow the example from the section "Implementation of a Dictionary with Hash-Table and Chaining". Read about quadratic probing in Wikipedia: http://en.wikipedia.org/wiki/Quadratic_probing. In order to expand the hash table (double its size), you can allocate an array with double size, transfer all the elements from the old one to the new one and at the end redirect the reference from the old array to the new one. To have foreach on your collection, implement the interface IEnumerable and inside your GetEnumerator() method you must return GetEnumerator() to the array of lists. You can use yield operator.
9. One way to solve the task is to use as key for the hash-table the element of the set and as a value always true. The union and intersection will be done by looping all the elements of the first set and checking if there is (respectively there is not) element of the second one.
10. Find all the members of the three sequences inside the given range and using HashSet<int> implement union and intersection of sets after that. At the end do the calculations requested.
11. TreeMultiSet<T> class you can implement by using the .NET system class SortedDictionary<K, List<T>>. It is not so easy, so take enough time to write the code and test it.
12. The obvious solution is to check for all the buses whether they arrive or depart in the given range. But according to the task terms we have to use HashSet<T>. Let’s think how.
With a linear scan (a for-loop) we can find all buses arriving after the beginning of the range and find all buses departing before the end of the range. These are two separate sets, right? The intersection of these sets should give us the set of buses we need.
If TimeInterval is a class, keeping the schedule of a bus (arriveHour, arriveMinute, departureHour, departureMinute), the intersection could be efficiently found by HashSet<TimeInterval> with correctly defined GetHashCode() and Equals().
Another, efficient solution is to use SortedSet<T> and its method GetViewBetween(<start>, <end>), but this contradicts to the problem description (recall that we are assigned to use HashSet<T>).
13. The first idea for a solution is simple: Using two nested loops we find all lucky sub-sequences of the sequence P. After that we sort them by their length (and by their elements as second criteria) and at the end we print the first 10. However, this algorithm will not work well if we have millions of sub-sequences. It may cause “out of memory”.
We would describe an idea for a much efficient solution: we will first define a class Sequence<T> to hold a sequence of elements. We will implement IComparable<Sequence<T>> to compare sequences by length in decreasing order (and by elements in decreasing order when the length is the same).
Later we will use our TreeMultiSet<T> class. Inside we will keep the first 10 sub-sequences of S, i.e. multi-set of the lucky sub-sequences of P, kept in decreasing order by length (and in decreasing order of their content when the length is the same). When we have 10 sub-sequences inside the multi-set and we add 11th sequence, it would take its correct place in the order, because of the IComparable<Sequence<T>> defined. After that we can delete the 11th subsequence, because it is not amongst the first 10. In that way we would always keep the first 10 elements, discarding the others in any given moment, consuming much less memory and with no need of sorting at the end. The implementation is not so easy, so spare enough time for it.
Demonstrations (source code)
Download the demo examples for this chapter from the book: Dictionaries,Hash-Tables-and-Sets-Demos.zip.
Discussion Forum
Comment the book and the tasks in the : forum of the Software Academy.
Tags: ADTs dictionary, balanced search tree, collisions, dictionaries and sets, Dictionary Data Structure, hash-tables, hashing, implementations with hash-tables and balanced trees, The "Set" Data Structure5 responses to “Chapter 18. Dictionaries, Hash-Tables and Sets”
Leave a Reply
You must be logged in to post a comment.
[…] Chapter 18. Dictionaries, Hash-Tables and Sets […]
Your post gave me a divine breakthrough in my project.I highly appreciate
Could you please shed more light on how you implemented the following:
class CaseInsensitiveComparer : IComparer
{
public int Compare(string s1, string s2)
{
return string.Compare(s1, s2, true);
}
}
Let’s use this interface IComparer when creating the dictionary:
IDictionary words =
new SortedDictionary(
new CaseInsensitiveComparer());
I tried to modify the previous code to run this IComparer, but it just did not work. Kindly help.
Node
Please ask in the forum: https://softuni.bg/forum
Sorry for the bother. I got it fixed! Now working fine