Chapter 7. Arrays
In this chapter we will learn about arrays as a way to work with sequences of elements of the same type. We will explain what arrays are, how we declare, create, instantiate and use them. We will examine one-dimensional and multidimensional arrays. We will learn different ways to iterate through the array, read from the standard input and write to the standard output. We will give many example exercises, which can be solved using arrays and we will show how useful they really are.
Content
- Video
- Presentation
- Mind Maps
- In This Chapter
- What Is an "Array"?
- Declaration and Allocation of Memory for Arrays
- Access to the Elements of an Array
- Reading an Array from the Console
- Printing an Array to the Console
- Iteration through Elements of an Array
- Multidimensional Arrays
- Arrays of Arrays
- Exercises
- Solutions and Guidelines
- Demonstrations (source code)
- Discussion Forum
Video
Presentation
Mind Maps
Arrays are vital for most programming languages. They are collections of variables, which we call elements:
An array’s elements in C# are numbered with 0, 1, 2, … N-1. Those numbers are called indices. The total number of elements in a given array we call length of an array.
All elements of a given array are of the same type, no matter whether they are primitive or reference types. This allows us to represent a group of similar elements as an ordered sequence and work on them as a whole.
Arrays can be in different dimensions, but the most used are the one-dimensional and the two-dimensional arrays. One-dimensional arrays are also called vectors and two-dimensional are also known as matrices.
Declaration and Allocation of Memory for Arrays
In C# the arrays have fixed length, which is set at the time of their instantiation and determines the total number of elements. Once the length of an array is set we cannot change it anymore.
Declaring an Array
We declare an array in C# in the following way:
|
int[] myArray; |
In this example the variable myArray is the name of the array, which is of integer type (int[]). This means that we declared an array of integer numbers. With [] we indicate, that the variable, which we are declaring, is an array of elements, not a single element.
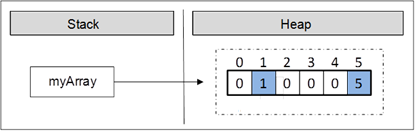
When we declare an array type variable, it is a reference, which does not have a value (it points to null). This is because the memory for the elements is not allocated yet.
The figure below shows how a declared array variable looks, when the memory for elements of the array is not allocated yet:
In the program’s execution stack the variable with the name myArray is created and its value is set to null (meaning it holds no value).
Creation of an Array – the Operator "new"
In C# we create an array with the help of the keyword new, which is used to allocate memory:
|
int[] myArray = new int[6]; |
In this example we allocate an array with length of 6 elements of type int. This means that in the dynamic memory (heap) an area of 6 integer numbers is allocated and they all are initialized with the value 0:
The figure shows, that after the allocation of memory for the array the variable myArray points to an address in the dynamic memory, where the values are. In C#, the elements of an array are always stored in the dynamic memory (called also heap).
During the allocation of the memory for an array we set the total number of the elements in the brackets (a non-negative integer number), defining its length. The type of the elements is written after the reserved word new, so we indicate what type of elements are going to be allocated in the memory.
Array Initialization and Default Values
Before we can use an element of a given array, it has to be initialized or to have a default value. In some programming languages there are no default values and then if we try to access an element, which is not initialized, this may cause an error. In C# all variables, including the elements of arrays have a default initial value. This value is either 0 for the numeral types or its equivalent for the non-primitive types (for example null for a reference type and false for the bool type).
Of course we can set initial values explicitly. We can do this in different ways. Here is one of them:
|
int[] myArray = { 1, 2, 3, 4, 5, 6 }; |
In this case we create and initialize the elements of the array at the time of the declaration. On the figure below we see how the array is allocated in the memory when its values are initialized at the moment of its declaration:
With this syntax we use curly brackets instead of the operator new. Between the brackets we list the initial values of the array, separated by commas. Their count defines the length of the array.
Declaration and Initialization of an Array – Example
Here is one more example how to declare and initialize an array:
|
string[] daysOfWeek = { "Monday", "Tuesday", "Wednesday","Thursday", "Friday", "Saturday", "Sunday" }; |
In this case we allocate an array of seven elements of type string. The type string is a reference type (object) and its values are stored in the dynamic memory. The variable daysOfWeek is allocated in the stack memory, and points to a section of the dynamic memory containing the elements of the array. The type of each of these seven elements is string, which itself points to a different section of the dynamic memory, where the real value is stored.
On this figure we see how the array is allocated in the memory:
Boundaries of an Array
Arrays are by default zero-based, which means the enumeration of the elements starts from 0. The first element has the index 0, the second – 1, etc. In an array of N elements, the last element has the index N-1.
Access to the Elements of an Array
We access the array elements directly using their indices. Each element can be accessed through the name of the array and the element’s index (consecutive number) placed in the brackets. We can access given elements of the array both for reading and for writing, which means we can treat elements as variables.
Here is an example for accessing an element of an array:
|
myArray[index] = 100; |
In the example above we set a value of 100 to the element, which is at position index.
Here is an example, where we allocate an array of numbers and then we change some of them:
|
int[] myArray = new int[6]; myArray[1] = 1; myArray[5] = 5; |
After the change, the array is allocated in the memory as shown below:
As we can see, all elements, except those for which values are explicitly set, are initialized with the value 0 when the memory of the array was allocated.
We can iterate through the array using a loop statement. The most common form of such iteration is by using a for-loop:
|
int[] arr = new int[5]; for (int i = 0; i < arr.Length; i++) { arr[i] = i; } |
Going Out of Bounds of the Array
The .NET Framework does an automatic check on each element access attempt, whether the index is valid or it is out of the range of the array. When we try to access an invalid (not existing) element in an array, a System.IndexOutOfRangeException is thrown. The automatic check really helps the developers find errors while working with arrays. Of course, checking for exceptions has its price. Checks affect the performance, but that’s nothing compared to avoiding errors like "out of range", "access to unallocated memory", etc.
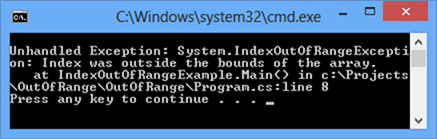
Here is an example, where we are trying to access an element, which is out of the range of the array:
|
IndexOutOfRangeExample.cs |
|
class IndexOutOfRangeExample { static void Main() { int[] myArray = { 1, 2, 3, 4, 5, 6 }; Console.WriteLine(myArray[6]); } } |
In the example above we allocate an array, which contains six integer numbers. The first index is 0, and the last index is 5. We are trying to print to the console an element with index 6, but because there is no such element this leads to an exception:
Reversing an Array – Example
In the next example we will access elements and change them using their indices. The task is to print the elements in reversed order. We will reverse the elements of the array using a second, auxiliary array, where we will keep the elements of the first one, but in a reversed order. Note that the length of both arrays is the same and it stays unchanged after the first allocation:
|
ArrayReverseExample.cs |
|
class ArrayReverseExample { static void Main() { int[] array = { 1, 2, 3, 4, 5 }; // Get array size int length = array.Length; // Declare and create the reversed array int[] reversed = new int[length];
// Initialize the reversed array for (int index = 0; index < length; index++) { reversed[length - index - 1] = array[index]; }
// Print the reversed array for (int index = 0; index < length; index++) { Console.Write(reversed[index] + " "); } } } // Output: 5 4 3 2 1 |
The example works in the following way: initially we allocate a one-dimensional array of type int and we initialize it with the numbers from 1 to 5. After that we keep the length of the array in the variable length. Note that we are using the property Length, which returns the total count of the elements of the array. In C# each array has a length property.
After that we declare the array reversed with the same length, where we will keep elements of the original array, but in a reversed order.
To reverse the elements we use a for-loop. At each iteration we increment the index variable by one and we make sure we access all consecutive elements of the array. The loop condition ensures that the array will be iterated from end to end.
Let’s follow what happens when we iterate through the array. On the first iteration, index has a value of 0. Using array[index] we access the first element of the array, and respectively with reversed[length - index - 1] we access the last element of the new array reversed where we assign the values. Thus, we appropriated the value of the first element of the array to the last element of the reversed array. At each iteration index is incremented by one. This way, we access the next element in the order of array and the previous element in the order of reversed.
As a result we reversed the array and printed it. In the example we showed consecutive iterations through the array, which can also be done with different types of loop constructs (e.g. while and foreach).
Reading an Array from the Console
Let’s see how we can read values of an array from the console. We will use a for-loop and the .NET Framework tools for reading from the console.
Initially we read a line from the console using Console.ReadLine(), and then we parse that line to an integer number using int.Parse() and we set it to the variable n. We then use the number n as length of the array.
|
int n = int.Parse(Console.ReadLine()); int[] array = new int[n]; |
Again we use a loop to iterate through the array. At each iteration we set the current element to what we have read from the console. The loop will continue n times, which means it will iterate through the array and so we will read a value for each element of the array:
|
for (int i = 0; i < n; i++) { array[i] = int.Parse(Console.ReadLine()); } |
Check for Symmetric Array – Example
An array is symmetric if the first and the last elements are equal and at the same time the second element and the last but one are equal as well and so on. On the figure a few examples for symmetric arrays are shown:
In the next example we will check whether an array is symmetric:
|
Console.Write("Enter a positive integer: "); int n = int.Parse(Console.ReadLine()); int[] array = new int[n];
Console.WriteLine("Enter the values of the array:");
for (int i = 0; i < n; i++) { array[i] = int.Parse(Console.ReadLine()); }
bool symmetric = true; for (int i = 0; i < array.Length / 2; i++) { if (array[i] != array[n - i - 1]) { symmetric = false; break; } }
Console.WriteLine("Is symmetric? {0}", symmetric); |
We initialize an array and we read its elements from the console. We need to iterate through half of the array to check whether it is symmetric. The middle element of the array has an index array.Length / 2. If the length is an odd number this index is exactly the middle one, but if it is an even number, the index is to the right of the middle (the middle is between two elements). Thus the loop runs from 0 to array.Length / 2 (non-inclusive).
To check whether an array is symmetric, we use a bool variable, and initially assume that the array is symmetric. During the iteration through the array we compare the first with the last element, the second with the last but one and so on. If at some point the compared elements are not equal, then we set the bool variable to false, which means the array is not symmetric.
In the end we print the value of the bool variable to the console.
Printing an Array to the Console
Often we have to print the elements of a given array to the console, after we have finished working with it.
We print elements of an array to the console similarly to the initializing of the elements, i.e. by using a loop to iterate through the array. There are no strict rules for printing, but often some sort of suitable formatting is used.
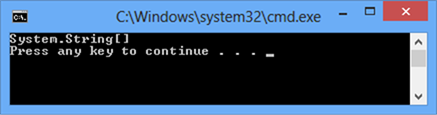
A frequent mistake is an attempt to print an array like a number:
|
string[] array = { "one", "two", "three", "four" }; Console.WriteLine(array); |
Unfortunately this code does not print the elements of an array, just its type. Here is what we get after the execution of this code:
We print the elements of an array by hand, by using a for-loop:
|
string[] array = { "one", "two", "three", "four" };
for (int index = 0; index < array.Length; index++) { // Print each element on a separate line Console.WriteLine("Element[{0}] = {1}", index, array[index]); } |
We are iterating through the array using the for-loop, which will go array.Length times, and we will print the current element using Console.WriteLine() and a formatted string. Here is the result:
|
Element[0] = one Element[1] = two Element[2] = three Element[3] = four |
Iteration through Elements of an Array
As we can see, the iteration through the elements of an array is one of the most used techniques when we work with arrays. Consecutive iterating using a loop will allow us to access each element through its index and we will be able to modify it as we want. We can do that with different loop constructs, but the most appropriate loop is the for-statement. We will examine in details how this type of iteration works.
Iteration with a For Loop
It is a good practice to use for-loops, when we work with arrays and structures with indices. In the following example we will double the values of all elements of an array of numbers and we will print them:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Output: "); for (int index = 0; index < array.Length; index++) { // Doubling the number array[index] = 2 * array[index]; // Print the number Console.Write(array[index] + " "); } // Output: 2 4 6 8 10 |
Using a for-loop we keep track of the current index of the array and we access the elements as needed. We do not have to iterate consecutively through all of them, which means the index that we are using in the for-loop may iterate through the elements in a way that our algorithm requires. For example we can iterate through some of the elements of the array, not through all of them:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Output: "); for (int index = 0; index < array.Length; index += 2) { array[index] = array[index] * array[index]; Console.Write(array[index] + " "); } // Output: 1 9 25 |
In this example we are iterating through all elements at even positions and we square their values.
Sometimes we want to iterate through the array in a reverse order. We do that in a similar way, except that the for-loop will start with the index of the last element and the index will decrease on each step until its value gets to 0 (inclusive). Here is an example:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Reversed: "); for (int index = array.Length - 1; index >= 0; index--) { Console.Write(array[index] + " "); } // Reversed: 5 4 3 2 1 |
In this example we are iterating through the array in reverse order and we print each element to the console.
Iteration with "foreach" Loop
One of the most used constructs for iterating through elements of an array is foreach. The foreach-loop construct in C# is as follows:
|
foreach (var item in collection) { // Process the value here } |
In this programming construct var is the type of the elements, which we iterate through. The collection is the array (or any other collection of elements) and item is the current element of the array on each step.
In general the foreach loop construct has the same properties like the for-loop. The main difference is that the iteration is made always through all elements – from the start to the end. We cannot access the current index, we are just iterating through the collection in a way, defined by the collection itself. For arrays the order of iteration is consecutive from the first element to the last one. The loop variable in foreach-loops is read-only so we cannot modify the current loop item from the loop body.
The foreach-loop statement is used, when we do not need to change the elements, but just to read them.
Iteration with "foreach" Loop – Example
In the next example we will learn how to use the foreach loop to iterate through the array:
|
string[] capitals = { "Sofia", "Washington", "London", "Paris" };
foreach (string capital in capitals) { Console.WriteLine(capital); } |
After we declared an array of strings capitals, we iterate through the array using foreach loop and we print the elements to the console. The current element on each step is stored in a variable capital. We get the following result when we execute the code:
|
Sofia Washington London Paris |
The one-dimensional arrays are known also as vectors in mathematics. Often we need arrays with more than one dimension. For example we can easily represent the standard chess board as a two-dimensional array with size 8 by 8 (8 cells in a horizontal direction and 8 cells in a vertical direction).
What Is a Multidimensional Array? What Are Matrices?
Every valid type in C# can be used for a type of an array. So, we can have an array of arrays, which we will discuss later.
We declare a one-dimensional array of integer numbers using int[], and we declare a two-dimensional with int[,]. This example shows that:
|
int[,] twoDimensionalArray; |
Those arrays we will call two-dimensional, because they have two dimensions. They are also known as matrices (it is mathematical term). In general arrays with more than one dimension we will call multidimensional.
This way we can declare three-dimensional arrays as we add one more dimension:
|
int[,,] threeDimensionalArray; |
In theory there is no limit for an array dimensions, but in practice we do not use much arrays with more than two dimensions therefore we will focus on two-dimensional arrays.
Multidimensional Array Declaration and Allocation
We declare multidimensional arrays in a way similar to one-dimensional arrays. Each dimension except the first is marked with comma:
|
int[,] intMatrix; float[,] floatMatrix; string[,,] strCube; |
In the example above we create two-dimensional and three-dimensional arrays. Each dimension is represented by a comma in the square brackets [].
We are allocating memory for multidimensional arrays by using the keyword new and for each dimension we set a length in the brackets as shown:
|
int[,] intMatrix = new int[3, 4]; float[,] floatMatrix = new float[8, 2]; string[,,] stringCube = new string[5, 5, 5]; |
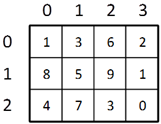
In this example intMatrix is a two-dimensional array with 3 elements of type int[] and each of those 3 elements has a length of 4. Two-dimensional arrays are difficult to understand explained that way. Therefore we can imagine them as two-dimensional matrices, which have rows and columns for the dimensions:
The rows and the columns of the square matrices are numbered with indices from 0 to n-1. If a two-dimensional array has a size of m by n, there are exactly m*n elements.
Two-Dimensional Array Initialization
We initialize two-dimensional arrays in the same way as we initialize one-dimensional arrays. We can list the element values straight after the declaration:
|
int[,] matrix = { {1, 2, 3, 4}, // row 0 values {5, 6, 7, 8}, // row 1 values }; // The matrix size is 2 x 4 (2 rows, 4 cols) |
In the example above we initialize a two-dimensional array of type integer with size of 2 rows and 4 columns. In the outer brackets we place the elements of the first dimension, i.e. the rows of the array. Each row contains one dimensional array, which we know how to initialize.
Accessing the Elements of a Multidimensional Array
Matrices have two dimensions and respectively we access each element by using two indices: one for the rows and one for the columns. Multidimensional arrays have different indices for each dimension.
|
Each dimension in a multidimensional array starts at index 0. |
Let’s examine the next example:
|
int[,] matrix = { {1, 2, 3, 4}, {5, 6, 7, 8}, }; |
The array matrix has 8 elements, stored in 2 rows and 4 columns. Each element can be accessed in the following way:
|
matrix[0, 0] matrix[0, 1] matrix[0, 2] matrix[0, 3] matrix[1, 0] matrix[1, 1] matrix[1, 2] matrix[1, 3] |
In this example we can access each element using indices. If we assign the index for rows to row, and the index for columns to col, then we can access any element as shown:
|
matrix[row, col] |
When we use multidimensional arrays each element is unique and can be identified with indices from the array:
|
nDimensionalArray[index1, …, indexN] |
Length of Multidimensional Arrays
Each dimension of a multidimensional array has its own length, which can be accessed during the execution of the program. Let’s look at an example for a two-dimensional array:
|
int[,] matrix = { {1, 2, 3, 4}, {5, 6, 7, 8}, }; |
We can get the number of the rows of this two-dimensional array by using matrix.GetLength(0) and the number of all columns per row with matrix.GetLength(1). So, in this case matrix.GetLength(0) returns 2 and matrix.GetLength(1) returns 4.
Printing Matrices – Example
In the next example we will demonstrate how we can print two-dimensional arrays to the console:
|
// Declare and initialize a matrix of size 2 x 4 int[,] matrix = { {1, 2, 3, 4}, // row 0 values {5, 6, 7, 8}, // row 1 value };
// Print the matrix on the console for (int row = 0; row < matrix.GetLength(0); row++) { for (int col = 0; col < matrix.GetLength(1); col++) { Console.Write(matrix[row, col]); } Console.WriteLine(); } |
First we declare and initialize an array, which we want to iterate through and print to the console. The array is two-dimensional, therefore we use a for-loop which will iterate through the rows and a nested for loop which for each row will iterate through the columns. At each iteration we will print the current element using the appropriate method to access this element by using its two indices (row and column). Finally, if we execute this piece of code we will get the following result:
|
1 2 3 4 5 6 7 8 |
Reading Matrices from the Console – Example
In this example we will learn how to read a two-dimensional array from the console. First, we read the values (lengths) of the two-dimensions and then by using two nested loops we assign the value of each element (and in the end we print out the values of the array):
|
Console.Write("Enter the number of the rows: "); int rows = int.Parse(Console.ReadLine());
Console.Write("Enter the number of the columns: "); int cols = int.Parse(Console.ReadLine());
int[,] matrix = new int[rows, cols];
Console.WriteLine("Enter the cells of the matrix:");
for (int row = 0; row < rows; row++) { for (int col = 0; col < cols; col++) { Console.Write("matrix[{0},{1}] = ",row, col); matrix[row, col] = int.Parse(Console.ReadLine()); } }
for (int row = 0; row < matrix.GetLength(0); row++) { for (int col = 0; col < matrix.GetLength(1); col++) { Console.Write(" " + matrix[row, col]); } Console.WriteLine(); } |
The program output when we execute it (in this case the array consists of three rows and two columns) is:
|
Enter the number of the rows: 3 Enter the number of the columns: 2 Enter the cells of the matrix: matrix[0,0] = 2 matrix[0,1] = 3 matrix[1,0] = 5 matrix[1,1] = 10 matrix[2,0] = 8 matrix[2,1] = 9 2 3 5 10 8 9 |
Maximal Platform in a Matrix – Example
In the next example we will solve another interesting problem: we are given a two-dimensional rectangular array (matrix) of integers and our task is to find the sub-matrix of size of 2 by 2 with maximum sum of its elements and to print it to the console.
One solution to the problem might be the following:
|
MaxPlatform2x2.cs |
|
class MaxPlatform2x2 { static void Main() { // Declare and initialize the matrix int[,] matrix = { { 0, 2, 4, 0, 9, 5 }, { 7, 1, 3, 3, 2, 1 }, { 1, 3, 9, 8, 5, 6 }, { 4, 6, 7, 9, 1, 0 } };
// Find the maximal sum platform of size 2 x 2 long bestSum = long.MinValue; int bestRow = 0; int bestCol = 0;
for (int row = 0; row < matrix.GetLength(0) - 1; row++) { for (int col = 0; col < matrix.GetLength(1) - 1; col++) { long sum = matrix[row, col] + matrix[row, col + 1] + matrix[row + 1, col] + matrix[row + 1, col + 1]; if (sum > bestSum) { bestSum = sum; bestRow = row; bestCol = col; } } }
// Print the result Console.WriteLine("The best platform is:"); Console.WriteLine(" {0} {1}", matrix[bestRow, bestCol], matrix[bestRow, bestCol + 1]); Console.WriteLine(" {0} {1}", matrix[bestRow + 1, bestCol], matrix[bestRow + 1, bestCol + 1]); Console.WriteLine("The maximal sum is: {0}", bestSum); } } |
If we execute the program, we will see that it works properly:
|
The best platform is: 9 8 7 9 The maximal sum is: 33 |
We will explain the algorithm. First we create a two-dimensional array, which contains integer numbers. We declare our auxiliary variables bestSum, bestRow, bestCol and we initialize bestSum with the minimal value of type long (so any other value is greater than this one). Note that sum of 4 integers may not fit in int, so we use long.
In the variable bestSum we keep the current maximal sum and in bestRow and bestCol we keep the current best sub-matrix. This means the current row and current column describe the start element for the sub-matrix of size 2 x 2, which is currently found to have the maximal sum of its elements.
To access all elements of a sub-array with a size of 2 by 2 we need the indices of the first element. Having them we can easily access the rest 3 elements:
|
matrix[row, col] matrix[row, col + 1] matrix[row + 1, col] matrix[row + 1, col + 1] |
In this example row and col are the indices of the first element of the sub-matrix with a size of 2 by 2, which is part of the array matrix.
After we know how to access all four elements of the matrix with a size of 2 by 2, starting from a particular row and column, we can look at the algorithm, which we will use to find the maximal sub-matrix.
We need to iterate through each 2 x 2 platform in the matrix until we reach the platform with the best sum. We will do this using two nested for-loops and two variables row and col. Note that we are not iterating through the entire matrix, because if we try to access index row + 1 or col + 1, as we are at the last row or column we will go out of the range of the matrix, respectively System.IndexOutOfRangeException will be thrown.
We access the neighbor elements of each current element of the sub-matrix and we sum them. Then we check if our current sum is bigger than our current highest sum for the moment. If it is so, our current sum becomes our best sum and our current indices will update bestRow and bestCol. So, after the entire iteration through the main matrix we will find the maximal sum and the first element of the sub-matrix of size 2 by 2 and its indices.
If there is more than one sub-matrix with the same maximal sum, we will find the one, which appears first.
At the end of the example we are printing to the console the requested sub-matrix of size 2 x 2 and its sum of elements in an appropriate way.
In C# we can have arrays of arrays, which we call jagged arrays.
Jagged arrays are arrays of arrays, or arrays in which each row contains an array of its own, and that array can have length different than those in the other rows.
Declaration and Allocation an Array of Arrays
The only difference in the declaration of the jagged arrays compared to the regular multidimensional array is that we do not have just one pair of brackets. With the jagged arrays we have a pair brackets per dimension. We allocate them this way:
|
int[][] jaggedArray; jaggedArray = new int[2][]; jaggedArray[0] = new int[5]; jaggedArray[1] = new int[3]; |
Here is how we declare, allocate and initialize an array of arrays (a jagged array whose elements are arrays of integer values):
|
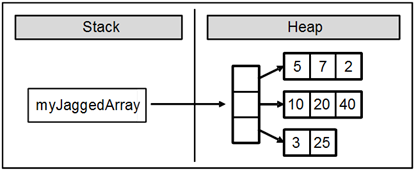
int[][] myJaggedArray = { new int[] {5, 7, 2}, new int[] {10, 20, 40}, new int[] {3, 25} }; |
Memory Allocation
The figure below depicts how the now declared jagged array myJaggedArray is allocated in the memory. As we see the jagged arrays are an aggregation of references. A jagged array does not directly contain any arrays, but rather has elements pointing to them. The size is unknown and that is why CLR just keeps references to the internal arrays. After we allocate memory for one array-element of the jagged array, then the reference starts pointing to the newly created block in the dynamic memory. The variable myJaggedArray is stored in the execution stack of the program and points to a block in the dynamic memory, which contains a sequence of three references to other three blocks in memory; each of them contains an array of integer numbers – the elements of the jagged array:
Initialization and Access to the Elements
We can access elements of the arrays, which are part of the jagged array by using their index. In next example we will access the element with index 3 of the array stored at index 0 in the myJaggedArray declared above:
|
myJaggedArray[0][2] = 45; |
The elements of the jagged array can be one-dimensional and multi-dimensional arrays. Here is an example for jagged array of two-dimensional arrays:
|
int[][,] jaggedOfMulti = new int[2][,]; jaggedOfMulti[0] = new int[,] { { 5, 15 }, { 125, 206 } }; jaggedOfMulti[1] = new int[,] { { 3, 4, 5 }, { 7, 8, 9 } }; |
Pascal’s Triangle – Example
In the next example we will use a jagged array to generate and visualize the Pascal’s triangle. As we know from mathematics, the first row of the triangle contains the number 1 and each next number is generated by sum of the two numbers on the row above it. The Pascal’s triangle looks like this:
|
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 . . . |
To have a Pascal’s triangle with a given height, for example 12, we allocate a jagged array triangle[][], which contains 1 element on the zero row, 2 – on first, 3 – on second and so on. First we initialize triangle[0][0] = 1 and the rest of the cells will have a default value than 0 by allocation. Then we loop through the rows and from row we will get the values for row+1. It works with nested for loop through the columns on the current row and the following Pascal definitions for values in the triangle: we add the value of the current cell of the current row (triangle[row][col]) to the cell below (triangle[row+1][col]) and to the cell below on the right (triangle
[row+1][col+1]). We print using an appropriate number of spaces (using method PadLeft () of class String), because we want the result to be aligned.
Here is the code of the described algorithm:
|
PascalTriangle.cs |
|
class PascalTriangle { static void Main() { const int HEIGHT = 12;
// Allocate the array in a triangle form long[][] triangle = new long[HEIGHT + 1][];
for (int row = 0; row < HEIGHT; row++) { triangle[row] = new long[row + 1]; }
// Calculate the Pascal's triangle triangle[0][0] = 1; for (int row = 0; row < HEIGHT - 1; row++) { for (int col = 0; col <= row; col++) { triangle[row + 1][col] += triangle[row][col]; triangle[row + 1][col + 1] += triangle[row][col]; } }
// Print the Pascal's triangle for (int row = 0; row < HEIGHT; row++) { Console.Write("".PadLeft((HEIGHT - row) * 2)); for (int col = 0; col <= row; col++) { Console.Write("{0,3} ", triangle[row][col]); } Console.WriteLine(); } } } |
If we execute the program, we will see that it is working properly and it generates a Pascal’s triangle by a given numbers of rows:
|
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 1 11 55 165 330 462 462 330 165 55 11 1 |
1. Write a program, which creates an array of 20 elements of type integer and initializes each of the elements with a value equals to the index of the element multiplied by 5. Print the elements to the console.
2. Write a program, which reads two arrays from the console and checks whether they are equal (two arrays are equal when they are of equal length and all of their elements, which have the same index, are equal).
3. Write a program, which compares two arrays of type char lexicographically (character by character) and checks, which one is first in the lexicographical order.
4. Write a program, which finds the maximal sequence of consecutive equal elements in an array. E.g.: {1, 1, 2, 3, 2, 2, 2, 1} à {2, 2, 2}.
5. Write a program, which finds the maximal sequence of consecutively placed increasing integers. Example: {3, 2, 3, 4, 2, 2, 4} à {2, 3, 4}.
6. Write a program, which finds the maximal sequence of increasing elements in an array arr[n]. It is not necessary the elements to be consecutively placed. E.g.: {9, 6, 2, 7, 4, 7, 6, 5, 8, 4} à {2, 4, 6, 8}.
7. Write a program, which reads from the console two integer numbers N and K (K<N) and array of N integers. Find those K consecutive elements in the array, which have maximal sum.
8. Sorting an array means to arrange its elements in an increasing (or decreasing) order. Write a program, which sorts an array using the algorithm "selection sort".
9. Write a program, which finds a subsequence of numbers with maximal sum. E.g.: {2, 3, -6, -1, 2, -1, 6, 4, -8, 8} à 11
10. Write a program, which finds the most frequently occurring element in an array. Example: {4, 1, 1, 4, 2, 3, 4, 4, 1, 2, 4, 9, 3} à 4 (5 times).
11. Write a program to find a sequence of neighbor numbers in an array, which has a sum of certain number S. Example: {4, 3, 1, 4, 2, 5, 8}, S=11 à {4, 2, 5}.
12. Write a program, which creates square matrices like those in the figures below and prints them formatted to the console. The size of the matrices will be read from the console. E.g. matrices with size of 4 x 4:
13. Write a program, which creates a rectangular array with size of n by m elements. The dimensions and the elements should be read from the console. Find a platform with size of (3, 3) with a maximal sum.
14. Write a program, which finds the longest sequence of equal string elements in a matrix. A sequence in a matrix we define as a set of neighbor elements on the same row, column or diagonal.
15. Write a program, which creates an array containing all Latin letters. The user inputs a word from the console and as result the program prints to the console the indices of the letters from the word.
16. Write a program, which uses a binary search in a sorted array of integer numbers to find a certain element.
17. Write a program, which sorts an array of integer elements using a "merge sort" algorithm.
18. Write a program, which sorts an array of integer elements using a "quick sort" algorithm.
19. Write a program, which finds all prime numbers in the range [1…10,000,000].
20. * Write a program, which checks whether there is a subset of given array of N elements, which has a sum S. The numbers N, S and the array values are read from the console. Same number can be used many times.
Example: {2, 1, 2, 4, 3, 5, 2, 6}, S = 14 à yes (1 + 2 + 5 + 6 = 14)
21. Write a program which by given N numbers, K and S, finds K elements out of the N numbers, the sum of which is exactly S or says it is not possible.
Example: {3, 1, 2, 4, 9, 6}, S = 14, K = 3 à yes (1 + 2 + 4 = 14)
22. Write a program, which reads an array of integer numbers from the console and removes a minimal number of elements in such a way that the remaining array is sorted in an increasing order.
Example: {6, 1, 4, 3, 0, 3, 6, 4, 5} à {1, 3, 3, 4, 5}
23. Write a program, which reads the integer numbers N and K from the console and prints all variations of K elements of the numbers in the interval [1…N]. Example: N = 3, K = 2 à {1, 1}, {1, 2}, {1, 3}, {2, 1}, {2, 2}, {2, 3}, {3, 1}, {3, 2}, {3, 3}.
24. Write a program, which reads an integer number N from the console and prints all combinations of K elements of numbers in range [1 … N]. Example: N = 5, K = 2 à {1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}.
25. *Write a program, which finds in a given matrix the largest area of equal numbers. We define an area in the matrix as a set of neighbor cells (by row and column). Here is one example with an area containing 13 elements with equal value of 3:
1. Use an int[] array and a for-loop.
2. Two arrays are equal if they have the same value for the length and the values for their elements. You can check for the second condition using a for-loop.
3. In lexicographic order the elements are compared one by one starting from the very left. If the elements are not the same, the array, whose element is smaller (comes earlier in the alphabet), comes first. If the elements are equal, the next character is compared. If the end of one of the arrays is reached, without finding different elements, the shorter array is the smaller (comes earlier lexicographically). If all elements are equal, the arrays are equal.
4. Scan the array from left to right. Every time when the current number is different from the one before it, a new sequence starts. If the current element is equal to the one before it, it is a continuation of the same sequence. So, if we keep the index of the start position of the current sequence (in the beginning it is 0) in start and the length of the current sequence (in the beginning it is 1) in len, we can find all sequences of equal elements and their lengths. We can easily keep the shortest one in two additional variables – bestStart and bestLen.
5. This exercise is very similar to the previous one, but we have a continuation of the current sequence when the next element is bigger.
6. We can solve the problem with two nested loops and one more array len[0…n-1]. In the array len[i] we can keep the length of the longest consecutively increasing sequence, which starts somewhere in the array (it does not matter where exactly) and ends with the element arr[i]. Therefore len[0]=1, len[x] is the maximal sum max(1 + len[prev]), where prev < x and arr[prev] < arr[x]. Following the definition, we can calculate len[0…n-1] with two nested loops: the outer loop will iterate through the array from left to right with the loop variable x. The inner loop will iterate through the array from the start to position x-1 and searches for the element prev with maximal value of len[prev], where arr[prev] < arr[x]. After the search, we initialize len[x] with 1 + the biggest found value of len[prev] or with 1, if such a value is not found.
The described algorithm finds the lengths of all maximal ascending sequences, which end at each of the elements. The biggest one of these values is the length of the longest increasing sequence. If we need to find the elements themselves, which compose that longest sequence, we can start from the element, where the sequence ends (at index x), we can print it and we can search for a previous element (prev). By definition prev < x and len[x] = 1 + len[prev] so we can find prev with a for-loop from 1 to x-1. After that we can repeat the same for x=prev. By finding and printing the previous element (prev) many times until it exists, we can find the elements, which compose the longest sequence in reversed order (from the last to the first).
7. You can find out which sequence of the sequences of K numbers has the biggest sum by checking the sums of all of those sequences. The first sequence starts at index 0 and finishes at index K-1 and has sum S. Then the second one starts at index 1 and ends at index K and we can find its sum using S by subtracting the element at index 0 and adding the element at index K. In this way we can reach the end of the sequence.
8. Find in Internet information about "Selection sort" and its C# implementations. Briefly the idea is to find the smallest element and to place it at position 0 (through swapping) then to find the smallest number excluding the first and place it at position 1 and so on, until the entire array is arranged in ascending order.
9. There are two ways to solve this problem. The first way is to use brute force method, which in this case means that using two nested loops we check every possible start and end and its corresponding sum.
The second way is to use one loop through the array to scan it from left to right and sum the elements. Once we get a negative sum, we can restart summing from the next element. Think why this is correct! At each step we check if the current sum is greater than the current max.
10. This exercise can be solved in a couple of ways. One of them is the following: get the first number and check how many times it is repeated in the array and store this number in a variable. After a repeated number is found we change its value to int.MinValue. Then pass to the next number and do the same with it. The current number is remembered if its occurrences are maximal. As you may guess, when a number equal to int.MinValue is found (already processed number) we should skip it.
Another solution is to sort the numbers in ascending order and then the elements with same value will be placed next to each other. So, basically we then find the longest sequence of neighbor equal elements.
11. This exercise can be solved with two nested loops. The first loop assigns a starting index. The second loop sums the elements from the starting index to the right until this partial sum reaches or is greater than S. If the sum is equal to S, we will remember the starting index (from the first loop) and the ending index (from the second loop).
If all numbers are positive, there is a much faster algorithm. We sum all numbers from left to the right, starting from zero. If the current sum becomes greater than S during the summation, we remove the leftmost number in the sequence and we subtract it from the sum. If the current sum is still greater than S, we remove the next leftmost number and do that until the current sum becomes smaller than S. When the sum becomes smaller than S we add the next number on right. If we find a sum equal to S, we print the sum and the sequence to the console. So this solution uses just with one scan through the elements in the array.
12. a), b), c) Think about appropriate ways for iterating through the matrices with two nested loops.
d) We can start from (0, 0) and go down N times. Therefore, go to the right N-1 times, after that up N-1 times, after that left N-2 times, after that down N-2 times and etc. At each iteration we place the next number in a sequence 1, 2, 3, …, N in the cell, which we are leaving.
13. Modify the example about maximal platform with size of 2 by 2.
14. Check every element in a diagonal line, a row and a column until you get a sequence. If you get a sequence, check whether this sequence is longer than the currently longest sequence.
15. We can solve this problem with two nested for-loops (one for the words and one for the letters of the current word). There is a solution without using an array: we can calculate the index of a given uppercase Latin letter ch using the expression: (int) ch – (int) 'A'.
16. Find on the Internet information about the algorithm "binary search". Note that binary search works only on sorted arrays.
17. Find on the Internet information about the algorithm "merge sort" and its implementations in C#. It is a bit complicated to write merge sort efficiently. You can have 3 preallocated arrays when merging arrays: two arrays for keeping the numbers for merging and а result array. Thus you will never allocate new arrays during the algorithm’s execution. The arrays will be allocated just once at the start and you will just change their purpose (swap them) during the algorithm execution.
18. Find information about the "quick sort" algorithm in Internet and its C# implementations. It can be best implemented by using recursion. See the chapter “Recursion” to read about recursive algorithms. Generally at each step you choose an element called pivot and reorder the array into two sections: at the left side move all elements ≤ pivot and at the right side move all elements > pivot. Finally run the quicksort algorithm recursively over the left and the right sides.
19. Find on the Internet information about "The sieve of Erathostenes" (you have probably heard about it in math classes in high-school).
20. Generate all possible sums this way: take all the numbers and mark them as "possible sum". Then take every number ko, k2, …, kn-1 and for each already marked "possible sum" p, mark as possible the sum p+ki. If at some step you get S, a solution is found. You can keep track of the "possible sums" either in a bool[] array possible[], where each index is a possible sum, or in a more complex data structure like Set<int>. Once you have possible[S] == true, you can find a number ki such that possible[S-ki] == true, print ki and subtract it from S. Repeat the same to find the next ki and print and subtract is again, until S reaches 0.
Another algorithm: generate all possible subsets of the numbers by a for-loop from 0 to 2N-1. If we have a number p, take its binary representation (which consists of exactly N bits) and sum the numbers that correspond to 1 in the binary representation of p (with a nested loop from 0 to N-1). Thus all possible sums will be generated and if some of them is S, it can be printed. Note that this algorithm is slow (needs exponential time and cannot run for 100 or 1000 elements). It also does not allow using the same array element twice in the sum.
21. See the previous problem. Generate all subsets of exactly K elements (the second algorithm) and check if their sum is equal to S.
Try in the first algorithm to think how to keep the count of the numbers used in the sum in order to take exactly K numbers. Can you define a matrix possible[p, n] to keep whether the number p can be obtained as a sum of the first n numbers (the numbers ko, k2, …, kn-1)?
22. Use dynamic programming to find the longest increasing sub-sequence in the input sequence arr[], just like in problem #6. The elements not included in the maximal increasing sequence should be removed in order the array to become sorted.
23. Start from the first variation in the lexicographical order: {1, 1, …} K times. Think of this as k-digit number. To obtain the next variation, increase the last digit. If it becomes greater than N, change it to 1 and increase the next digit on the left. Do the same on the left until the first digit goes greater than N.
24. Modify the algorithm from the previous problem in the following way: start from {1, 2, …, N} and increase the last digit (with the digits at the left when required), but always keep all elements in the array in ascending order (element p[i] should start increasing from p[i-1]+1).
25. This is a little bit more difficult. You can use different graph traversal algorithms like "DFS" (Depth-First-Search) and "BFS" (Breadth-First-Search) to go through all the cells in certain area starting from any cell that belongs to it. If you have an area traversal algorithm (like DFS), run it several times starting from unvisited cell and mark the cells of the traversed area as visited. Repeat this until all cells become visited. Read later in this book about DFS and BFS in the chapter “Trees and Graphs” or find information about these algorithms in Internet.
Demonstrations (source code)
Download the demo examples for this chapter from the book: Arrays-Demos.zip.
Discussion Forum
Comment the book and the tasks in the : forum of the Software Academy.
9 responses to “Chapter 7. Arrays”
Leave a Reply
You must be logged in to post a comment.

![clip_image002[13] clip_image002[13]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image00213_thumb.png)
![clip_image004[8] clip_image004[8]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0048_thumb.png)
![clip_image006[9] clip_image006[9]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0069_thumb.png)
![clip_image008[6] clip_image008[6]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0086_thumb.png)
![clip_image010[4] clip_image010[4]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0104_thumb.png)

![clip_image025[7] clip_image025[7]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0257_thumb.png)
![clip_image027[7] clip_image027[7]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0277_thumb.png)
![clip_image029[7] clip_image029[7]](https://introprogramming.info/wp-content/uploads/2013/07/clip_image0297_thumb.png)
[…] Chapter 7. Arrays […]
After months of lookin for a good C# website, I’ve finally the absolute best C# site. The explanations are thorough and not too slow and the questions are challenging and infomative. Whoever you are that’s responsible for this site, I cannot thank you enough.
The website is perfect for learning programming the right way! Comment to PascalTriangle.cs:
One row too much is allocated, it would suffice to do sth like this:
long[][] triangle[] = new long[HEIGHT][];
PJ Males s Stylish Slim Fit Hoodies Hooded Coat four Size
S~XL CL4493.
Thanks a lot.In a word this is great.
Java Array is very important topic from logic and java interview point of view. Here you explained java array in detail.
thanks you so much for this useful java array article.
hello everyone
i have been working on exercise number 20 in chapter 7 (arrays) , did anybody solve it , any help?
I love this programming bool but I have a request to the team of Fundamentals of Programming with C# to kindly add solutions to the exercises .I am a beginner
in C# programming and it is quite difficult for me to solve some of the problems.\
I hope you guys look forward to adding solution for this book
Please join the programming community at https://softuni.org. All questions will be answered.
Nakov