Глава 17. Дървета и графи
Автор
Веселин Колев
В тази тема...
В настоящата тема ще разгледаме т. нар. дървовидни структури от данни, каквито са дърветата и графите. Познаването на свойствата на тези структури е важно за съвременното програмиране. Всяка от тях се използва за моделирането на проблеми от реалността, които се решават ефективно с тяхна помощ. Ще разгледаме в детайли какво представляват дървовидните структури данни и ще покажем техните основни предимства и недостатъци. Ще дадем примерни реализации и задачи, демонстриращи реалната им употреба. Ще се спрем по-подробно на двоичните дървета, наредените двоични дървета за претърсване и балансираните дървета. Ще разгледаме структурата от данни "граф", видовете графи и тяхната употреба. Ще покажем как се работи с вградените в Java платформата имплементации на балансирани дървета.
Съдържание
- Автор
- В тази тема...
- Дървовидни структури
- Дървета
- Графи
- Упражнения
- Решения и упътвания
- Дискусионен форум
Видео
Презентация
Дървовидни структури
В много ситуации в ежедневието се налага да опишем (моделираме) съвкупност от обекти, които са взаимно свързани по някакъв начин и то така, че не могат да бъдат описани чрез досега изложените линейни структури от данни. В следващите няколко точки от тази тема ще дадем примери за такива структури, ще покажем техните свойства и съответно практическите задачи, които са довели до тяхното възникване.
Дървета
В програмирането дърветата са изключително често използвана структура от данни, защото те моделират по естествен начин всякакви йерархии от обекти, които постоянно ни заобикалят в реалния свят. Нека дадем един пример, преди да изложим терминологията, свързана с дърветата.
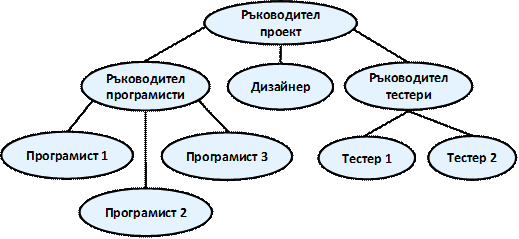
Пример – йерархия на участниците в един софтуерен проект
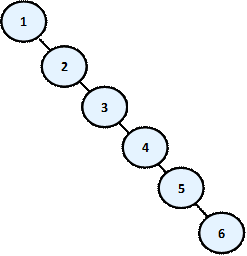
Да вземем за пример един екип, отговорен за изработването на даден софтуерен проект. Участниците в него са взаимно свързани с връзката ръководител-подчинен. Ще разгледаме една конкретна ситуация, в която имаме екип от 9 души:
Каква информация можем да извлечем от така изобразената йерархия? Прекият шеф на програмистите е съответно "Ръководител програмисти". "Ръководител проект" е също е техен началник, но непряк, т.е. те отново са му подчинени. "Ръководител програмисти" е подчинен само на "Ръководител проект". От друга страна, ако погледнем "Програмист 1", той няма нито един подчинен. "Ръководител проект" стои най-високо в йерархията и няма шеф.
По аналогичен начин можем да опишем и ситуацията с останалите участници в проекта. Виждаме как една на пръв поглед малка фигура ни носи много информация.
Терминология, свързана с дърветата
За по-доброто разбиране на тази точка силно препоръчваме на читателя да се опита на всяка стъпка да прави аналогия между тяхното абстрактно значение и това, което използваме в ежедневието.
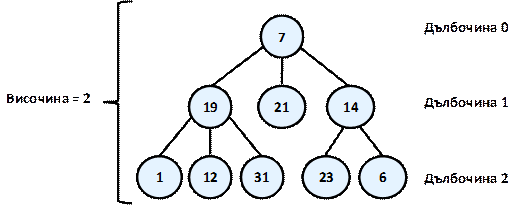
Нека да опростим начина, по който изобразихме нашата йерархия. Можем да приемем, че тя се състои от точки, свързани с отсечки. За удобство, точките ще номерираме с произволни числа, така че после лесно да можем да говорим за някоя конкретна.
Всяка една точка, ще наричаме връх, а всяка една отсечка – ребро. Върховете "19", "21" и "14" стоят под върха "7" и са директно свързани с него. Тях ще наричаме преки наследници (деца) на "7", а "7" – техен родител (баща). Аналогично "1", "12" и "31" са деца на "19" и "19" е техен родител. Съвсем естествено ще казваме, че "21" е брат на "19", тъй като са деца на "7" (обратното също е вярно – "19" е брат на "21"). От гледна точка на "1", "12", "31", "23" и "6", "7" е предшестващ ги в йерархията (в случая е родител на техните родители). Затова "7" ще наречем техен непряк предшественик (дядо, прародител), а тях – негови непреки наследници.
Корен е върхът, който няма предшественици. В нашия случай той е "7".
Листа са всички върхове, които нямат наследници. В примера – "1", "12", "31", "21", "23" и "6" са листа.
Вътрешни върхове са всички върхове, различни от корена и листата (т.е. всички върхове, които имат както родител, така и поне един наследник). Такива са "19" и "14".
Път ще наричаме последователност от свързани чрез ребра върхове, в която няма повтарящи се върхове. Например последователността "1", "19", "7" и "21" е път. "1", "19" и "23" не е път, защото "19" и "23" не са свързани помежду си с ребро.
Дължина на път е броят на ребрата, свързващи последователността от върхове в пътя. Практически този брой е равен на броят на върховете в пътя минус единица. Дължината на примера ни за път ("1", "19", "7" и "21") е три.
Дълбочина на връх ще наричаме дължината на пътя от корена до дадения връх. На примера ни "7" като корен е с дълбочина нула, "19" е с дълбочина едно, а "23" – с дълбочина две.
И така, ето и дефиницията за това какво е дърво:
Дърво (tree) – рекурсивна структура от данни, която се състои от върхове, които са свързани помежду си с ребра. За дърветата са в сила твърденията:
- Всеки връх може да има 0 или повече преки наследници (деца).
- Всеки връх има най-много един баща. Съществува точно един специален връх, който няма предшественици – коренът (ако дървото не е празно).
- Всички върхове са достижими от корена, т.е съществува път от корена до всички тях.
Можем да дефинираме дърво и по по-прост начин: всеки единичен връх наричаме дърво и той може да има нула или повече наследници, които също са дървета.
Височина на дърво е максималната от дълбочините на всички върхове. В горния пример височината е 2.
Степен на връх ще наричаме броят на преките наследници (деца) на дадения връх. Степента на "19" и "7" е три, докато тази на "14" е две. Листата са от нулева степен.
Разклоненост на дърво се нарича максималната от степените на всички върхове в дървото. В нашият пример степента на върховете е най-много 3, следователно разклонеността на дървото ни е 3.
Реализация на дърво – пример
Нека сега разгледаме как можем да представяме дърветата като структури от данни в програмирането. Ще реализираме дърво, което съдържа числа във върховете си и всеки връх може да има 0 или повече наследници, които също са дървета (следвайки рекурсивната дефиниция). Всеки връх от дървото е рекурсивно-дефиниран чрез себе си. Един връх от дървото (TreeNode<T>) съдържа в себе си списък от наследници, които също са върхове от дървото (TreeNode<T>). Нека разгледаме сорс кода:
|
import java.util.ArrayList;
/** * Represents a tree data structure. * @author Vesko Kolev * @param <T> - the type of the values in the tree. */ public class Tree<T> { /** * Represents a tree node. * @author Vesko Kolev * @param <T> - the type of the values in nodes. */ public static class TreeNode<T> { // Contains the value of the node private T value;
// Shows whether the current node has parent private boolean hasParent;
// Contains the children of the node private ArrayList<TreeNode<T>> children;
/** * Constructs a tree node. * @param value - the value of the node. */ public TreeNode(T value) { if (value == null) { throw new IllegalArgumentException( "Cannot insert null value!"); } this.value = value; this.children = new ArrayList<TreeNode<T>>(); }
/** * @return the value of the node. */ public T getValue() { return this.value; }
/** * Sets the value of the node. * @param value - the value to be set. */ public void setValue(T value) { this.value = value; }
/** * Adds child to the node. * @param child - the child to be added. */ public void addChild(TreeNode<T> child) { if (child == null) { throw new IllegalArgumentException( "Cannot insert null value!"); }
if (child.hasParent) { throw new IllegalArgumentException( "The node already has a parent!"); }
child.hasParent = true; this.children.add(child); }
/** * Gets the child of the node at given index. * @param index - the index of the desired child. * @return the child on the given position. */ public TreeNode<T> getChild(int index) { return this.children.get(index); }
/** * @return the number of node's children. */ public int getChildrenCount() { return this.children.size(); } }
// The root of the tree private TreeNode<T> root;
/** * Constructs the tree. * @param value - the value of the node. */ public Tree(T value) { if (value == null) { throw new IllegalArgumentException( "Cannot insert null value!"); }
this.root = new TreeNode<T>(value); }
/** * Constructs the tree. * @param value - the value of the root node. * @param children - the children of the root node. */ public Tree(T value, Tree<T> ...children) { this(value);
for (Tree<T> child : children) { this.root.addChild(child.root); } }
/** * @return the root node or null if the tree is empty. */ public TreeNode<T> getRoot() { return this.root; }
/** * @return the child nodes of the tree. */ public ArrayList<TreeNode<T>> getChildNodes() { if (this.root != null) { return this.root.children; } return new ArrayList<TreeNode<T>>(); }
/** * Traverses and prints tree in * Depth First Search (DFS) manner. * @param root - the root of the tree * to be traversed. * @param spaces - the spaces used for * representation of the parent-child relation. */ private void printDFS(TreeNode<T> root, String spaces) { if (this.root == null) { return; }
System.out.println(spaces + root.getValue());
TreeNode<T> child = null; for (int i = 0; i < root.getChildrenCount(); i++) { child = root.getChild(i); printDFS(child, spaces + " "); } }
/** * Traverses and prints the tree in * Depth First Search (DFS) manner. */ public void printDFS() { this.printDFS(this.root, new String()); } }
/** * Shows a sample usage of the Tree<E> class. * @author Vesko Kolev */ public class TreeExample { public static void main(String[] args) { // Create the tree from the sample Tree<Integer> tree = new Tree<Integer>(7, new Tree<Integer>(19, new Tree<Integer>(1), new Tree<Integer>(12), new Tree<Integer>(31)), new Tree<Integer>(21), new Tree<Integer>(14, new Tree<Integer>(23), new Tree<Integer>(6)) );
// Traverse and print the tree using Depth-First-Search tree.printDFS();
// Console output: // 7 // 19 // 1 // 12 // 31 // 21 // 14 // 23 // 6 } } |
Как работи нашата имплементация на дърво?
Нека кажем няколко думи за предложения код. В примера имаме клас Tree<Т>, който е имплементация на самото дървото. В него е дефиниран вътрешен клас – TreeNode<T>, който представлява един връх от дървото.
Функционалността, свързана с връх като например създаване на връх, добавяне на наследник на връх, взимане на броя на наследниците и т.н. се реализират на ниво TreeNode<T>.
Останалата функционалност (например обхождане на дървото) се реализира на ниво Tree<Т>. Така функционалността става логически разделена между двата класа, което прави имплементацията по гъвкава.
Причината да разделим на два класа имплементацията е, че някои операции се отнасят за конкретен връх (например добавяне на наследник), докато други се отнасят за цялото дърво (например търсене на връх по неговата стойност). При такова разделяне дървото е клас, който знае кой му е коренът, а всеки връх знае наследниците си. При такава имплементация е възможно да имаме и празно дърво (при root=null).
Ето и някои подробности от реализацията на TreeNode<T>. Всеки един връх (node) на дървото представлява съвкупност от частно поле value, което съдържа стойността му, и списък от наследници children. Списъкът на наследниците е от елементи на същия тип. Така всеки връх съдържа списък от референции към неговите преки наследници. Предоставени са също get и set методи за достъп до стойността на върха. Операциите, които могат да се извършват от външен за класа код върху децата, са:
- addChild(TreeNode<T> child) - добавя нов наследник.
- TreeNode<T> getChild(int index) - връща наследник по зададен индекс.
- getChildrenCount() - връща броя на наследници на даден връх.
За да спазим изискването всеки връх в дървото да има точно един родител, сме дефинирали частното поле hasParent, което показва дали даденият връх има родител. Тази информация се използва вътрешно в нашия клас и ни трябва в метода addChild(Tree<E> child). В него правим проверка дали кандидат детето няма вече родител. Ако има, се хвърля изключение, показващ, че това е недопустимо.
В класа Tree<Т> сме предоставили два get метода TreeNode<T> getRoot() и ArrayList<TreeNode<T>> getChildNodes(), които връщат съответно корена на дървото и неговите преки наследници (деца).
Рекурсивно обхождане на дърво в дълбочина
В класа Tree<Т> e реализиран е и методът TraverseDFS(), който извиква частният метод DFS(TreeNode<E> root, String spaces), който обхожда дървото в дълбочина и извежда на стандартният изход елементите му, така че нагледно да се изобрази дървовидната структура чрез отместване надясно (с добавяне на интервали).
Алгоритъмът за обхождане в дълбочина (Depth-First-Search или DFS) започва от даден връх и се стреми да се спусне колкото се може по-надолу в дървовидната йерархия и когато стигне до връх, от който няма продължение се връща назад към предходния връх. Алгоритъмът можем да опишем схематично по следния начин:
1. Обхождаме текущия връх.
2. Последователно обхождаме рекурсивно всяко едно от поддърветата на текущия връх (обръщаме се рекурсивно към същия метод последователно за всеки един от неговите преки наследници).
Създаване на дърво
За да създаваме по-лесно дървета сме дефинирали специален конструктор, който приема стойност на връх и списък от поддървета за този връх. Така позволяваме подаването на произволен брой аргументи от тип Tree<E> (поддървета). При създаването на дървото за нашия пример използваме точно този конструктор и той ни позволява да онагледим структурата му.
Обхождане на директориите по твърдия диск
Нека сега разгледаме още един пример за дърво – файловата система. Замисляли ли сте се, че директориите върху твърдия ви диск образуват йерархична структура, която е дърво? Можете да се сетите и за много други реални примери, при които се използват дървета.
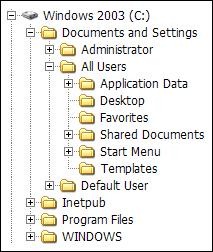
Нека разгледаме по-подробно файловата система в Windows. Както знаем от нашия всекидневен опит, ние създаваме папки върху твърдия диск, които могат да съдържат от своя страна подпапки или файлове. Подпапките отново може да съдържат подпапки и т. н. до някакво разумно ограничение (максимална дълбочина).
Дървото на файловата система е достъпно чрез стандартни функции от класа java.io.File. То не съществува като структура от данни в явен вид, но съществува начин да извличаме за всяка директория файловете и директориите в нея и следователно можем да го обходим чрез стандартен алгоритъм за обхождане на дървета.
Ето как изглежда типичното дърво на директориите в Windows:
Рекурсивно обхождане на директориите в дълбочина
Следващият пример показва как да обходим рекурсивно (в дълбочина, по алгоритъмa Depth-First-Search) дървовидната структура на дадена папка и да изведем на стандартния изход и нейното съдържание:
|
DirectoryTraverserDFS.java |
|
import java.io.File;
/** * Sample class, which traverses recursively given directory * based on the Depth-First-Search (DFS) algorithm. * * @author Vesko Kolev */ public class DirectoryTraverserDFS { /** * Traverses and prints given directory recursively. * @param dir - the directory to be traversed. * @param spaces - the spaces used for representation * of the parent-child relation. */ private static void traverseDir(File dir, String spaces) {
// If the current element is a directory, // we get all it subdirectories and files if (dir.isDirectory()) { System.out.println(spaces + dir.getAbsolutePath()); String[] children = dir.list();
// For each child go and visit its subtree for (String child : children) { traverseDir(new File(dir, child), spaces + " "); } } }
/** * Traverses and prints given directory recursively. * @param directoryPath - the path to the directory which * should be traversed. */ public static void traverseDir(String directoryPath) { traverseDir(new File(directoryPath), new String()); }
public static void main(String[] args) { traverseDir("C:\\"); } } |
Както се вижда от примера, рекурсивното обхождане на съдържанието на директория по нищо не се различава от обхождането на нашето дърво. В случая, файловете представляват листа, началната директория – корен, а останалите директории – вътрешни върхове. Всъщност, ако една директория е празна, тогава тя също се явява листо, защото няма наследници.
Ето как изглежда резултатът от обхождането (със съкращения):
|
C:\ C:\Config.Msi C:\Documents and Settings C:\Documents and Settings\Administrator C:\Documents and Settings\Administrator\.ARIS70 C:\Documents and Settings\Administrator\.jindent C:\Documents and Settings\Administrator\.nbi C:\Documents and Settings\Administrator\.nbi\downloads C:\Documents and Settings\Administrator\.nbi\log C:\Documents and Settings\Administrator\.nbi\cache C:\Documents and Settings\Administrator\.nbi\tmp C:\Documents and Settings\Administrator\.nbi\wd C:\Documents and Settings\Administrator\.netbeans C:\Documents and Settings\Administrator\.netbeans\6.0 ... |
Обхождане на директориите в ширина
Нека сега разгледаме още един начин да обхождаме дървета. Обхождането в ширина (Breadth-First-Search или BFS) е алгоритъм за обхождане на дървовидни структури от данни, при който първо се посещава началният връх, след това неговите преки съседи, след тях преките съседи на съседите и т.н. Този процес метод на вълната, защото прилича на вълните, образувани от камък, хвърлен в езеро.
Алгоритъмът за обхождане на дърво в ширина по метода на вълната можем да опишем схематично по следния начин:
1. Записваме в опашката Q началния връх.
2. Докато Q не е празна повтаряме следните две стъпки:
- Изваждаме от Q поредния връх v и го отпечатваме.
- Добавяме всички наследници на v в опашката.
Алгоритъмът BFS е изключително прост и има свойството да обхожда първо най-близките до началния връх върхове, след тях по-далечните и т.н. и най-накрая – най-далечните върхове. С времето ще се убедите, че BFS алгоритъмът има широко приложение при решаването на много задачи, като например при търсене на най-кратък път в лабиринт.
Нека сега приложим BFS алгоритъма за отпечатване на всички директории от файловата система:
|
DirectoryTraverserBFS.java |
|
import java.io.File; import java.util.LinkedList; import java.util.Queue;
/** * Sample class, which traverses given directory * based on the Breadth-First-Search (BFS) algorithm. * @author Svetlin Nakov */ public class DirectoryTraverserBFS { /** * Traverses and prints given directory with BFS. * @param startDir - the path to the directory which * should be traversed. */ public static void traverseDir(String startDirectory) { Queue<File> visitedDirsQueue = new LinkedList<File>(); visitedDirsQueue.add(new File(startDirectory)); while (visitedDirsQueue.size() > 0) { File currentDir = visitedDirsQueue.remove(); System.out.println(currentDir.getAbsolutePath()); File[] children = currentDir.listFiles(); if (children != null) { for (File child : children) { if (child.isDirectory()) { visitedDirsQueue.add(child); } } } } }
public static void main(String[] args) { traverseDir("C:\\"); } } |
Ако стартираме програмата, ще се убедим, че обхождането в ширина първо открива най-близките директории до корена (дълбочина 1), след тях всички директории на дълбочина 2, след това директориите на дълбочина 3 и т.н. Ето примерен изход от програмата:
|
C:\ C:\Config.Msi C:\Documents and Settings C:\Inetpub C:\Program Files C:\RECYCLER C:\System Volume Information C:\WINDOWS C:\wmpub C:\Documents and Settings\Administrator C:\Documents and Settings\All Users C:\Documents and Settings\Default User ... |
Двоични дървета
В предишната точка от темата разгледахме обобщената структура дърво. Сега ще преминем към един неин полезен частен случай, който се оказва изключително важен за практиката – двоично дърво. Важно е да отбележим, че термините, които дефинирахме до момента, важат с пълна сила и при този вид дърво. Въпреки това по-долу ще дадем и някои допълнителни, специфични за дадената структура определения.
Двоично дърво (binary tree) – дърво, в което всеки връх е от степен не надвишаваща две т.е. дърво с разклоненост две. Тъй като преките наследници (деца) на всеки връх са най-много два, то е прието да се въвежда наредба между тях, като единият се нарича ляв наследник, а другият – десен наследник. Те от своя страна са корени съответно на лявото поддърво и на дясното поддърво на техния родител.
Двоично дърво – пример
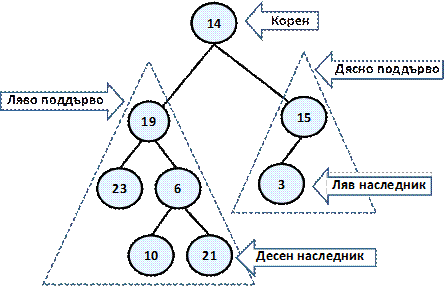
Ето и едно примерно двоично дърво, което ще използваме за изложението по-нататък. В този пример отново въвеждаме номерация на върховете, която е абсолютно произволна и която ще използваме, за да може по-лесно да говорим за всеки връх.
На примера са изобразени съответно коренът на дървото "14", пример за ляво поддърво (с корен "19") и дясно поддърво (с корен "15"), както и ляв и десен наследник – съответно "3" и "21".
Следва да отбележим обаче, че двоичните дървета имат едно много сериозно различие в дефиницията си, за разлика от тази на обикновеното дърво – наредеността на наследниците на всеки връх. Следващият пример ясно показва това различие:
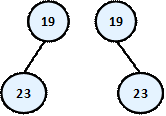
На схемата са изобразени две абсолютно различни двоични дървета – в единия случай коренът е "19" и има ляв наследник "23", а в другия имаме двоично дърво с корен отново "19", но с "23" за десен наследник. Ако разгледаме обаче двете структури като обикновени дървета, те ще са абсолютно еднакви и неразличими. Затова такова дърво бихме изобразили по следния начин:
|
Запомнете! Въпреки, че разглеждаме двоичните дървета като подмножество на структурата дърво, трябва да се отбележи, че условието за нареденост на наследниците ги прави до голяма степен различни като структури. |
Обхождане на двоично дърво
Обхождането на дърво по принцип е една класическа и често срещана задача. В случая на двоичните дървета има няколко основни начина за обхождане:
- ЛДК (Ляво-Корен-Дясно/Pre-order) – обхождането става като първо се обходи лявото поддърво, след това коренът и накрая дясното поддърво. В нашият пример последователността, която се получава при обхождането е: "23", "19", "10", "6", "21", "14", "3", "15".
- КЛД (Корен-Ляво-Дясно/In-order) – в този случай първо се обхожда коренът на дървото, после лявото поддърво и накрая дясното. Ето и как изглежда резултатът от този вид обхождане: "14", "19", "23", "6", "10", "21", "15", "3".
- ЛДК (Ляво-Дясно-Корен/Post-order) – тук по аналогичен на горните два примера начин, обхождаме първо лявото поддърво, после дясното и накрая коренът. Резултатът след обхождането е "23", "10", "21", "6", "19", "3", "15", "14".
Обхождане на двоично дърво с рекурсия – пример
В следващия пример ще покажем примерна реализация на двоично дърво, което ще обходим по схемата ЛДК:
|
/** * Represents a binary tree structure. * @author Vesko Kolev */ public class BinaryTree<T> {
/** * Represents a binary tree node. * @author Vesko Kolev * @param <T> - the type of the values in nodes. */ public static class BinaryTreeNode<T> { // Contains the value of the node private T value;
// Shows whether the current node has parent private boolean hasParent;
// Contains the left child of the node private BinaryTreeNode<T> leftChild;
// Contains the right child of the node private BinaryTreeNode<T> rightChild;
/** * Constructs a binary tree node. * @param value - the value of the node. * @param leftChild - the left child of the node. * @param rightChild - the right child of the node. */ public BinaryTreeNode(T value, BinaryTreeNode<T> leftChild, BinaryTreeNode<T> rightChild) { if (value == null) { throw new IllegalArgumentException( "Cannot insert null value!"); }
this.value = value; this.leftChild = leftChild; this.rightChild = rightChild; }
/** * Constructs a binary tree node with no children. * @param value - the value of the node. */ public BinaryTreeNode(T value) { this(value, null, null); }
/** * @return the value of the node. */ public T getValue() { return this.value; }
/** * Sets the value of the node. * @param value - the value to be set. */ public void setValue(T value) { this.value = value; }
/** * @return the left child or null if it does not exists. */ public BinaryTreeNode<T> getLeftChild() { return this.leftChild; }
/** * Sets the left child. * @param value - the new left child to be set. */ public void setLeftChild(BinaryTreeNode<T> value) { if (value == null || value.hasParent) { throw new IllegalArgumentException(); }
value.hasParent = true; this.leftChild = value; }
/** * @return the right child or null if it does not exists. */ public BinaryTreeNode<T> getRightChild() { return this.rightChild; }
/** * Sets the right child. * @param value - the new right child to be set. */ public void setRightChild(BinaryTreeNode<T> value) { if (value == null || value.hasParent) { throw new IllegalArgumentException(); }
value.hasParent = true; this.rightChild = value; } }
// The root of the tree private BinaryTreeNode<T> root;
/** * Constructs the tree. * @param value - the value of the node. * @param children - the children of the node. */ public BinaryTree(T value, BinaryTree<T> leftChild, BinaryTree<T> rightChild) { if (value == null) { throw new IllegalArgumentException(); }
BinaryTreeNode<T> leftChildNode = leftChild != null ? leftChild.root : null; BinaryTreeNode<T> rightChildNode = rightChild != null ? rightChild.root : null; this.root = new BinaryTreeNode<T>( value, leftChildNode, rightChildNode); }
/** * Constructs the tree. * @param value - the value of the node. */ public BinaryTree(T value) { this(value, null, null); }
/** * @return the root of the tree. */ public BinaryTreeNode<T> getRoot() { return this.root; }
/** * @return the left child of the root. */ public BinaryTreeNode<T> getLeftChildNode() { if (this.root != null) { return this.root.getLeftChild(); }
return null; }
/** * @return the right child of the root. */ public BinaryTreeNode<T> getRightChildNode() { if (this.root != null) { return this.root.getRightChild(); }
return null; }
/** * Traverses binary tree in pre-order manner. * @param root - the binary tree to be traversed. */ private void printPreOrder(BinaryTreeNode<T> root) { if (root == null) { return; }
// 1. Visit the left child. printPreOrder(root.getLeftChild());
// 2. Visit the root of this subtree. System.out.print(root.getValue() + " ");
// 3. Visit the right child. printPreOrder(root.getRightChild()); }
/** * Traverses and prints the binary * tree in pre-order manner. */ public void printPreOrder() { printPreOrder(this.root); System.out.println(); } }
/** * Shows how the BinaryTree class can be used. * @author Vesko Kolev */
public class BinaryTreeExample { public static void main(String[] args) { // Create the binary tree from the sample. BinaryTree<Integer> binaryTree = new BinaryTree<Integer>(14, new BinaryTree<Integer>(19, new BinaryTree<Integer> (23), new BinaryTree<Integer> (6, new BinaryTree<Integer>(10), new BinaryTree<Integer>(21))), new BinaryTree<Integer>(15, new BinaryTree<Integer>(3), null));
// Traverse and print the tree in pre-order manner. binaryTree.printPreOrder();
// Console output: // 23 19 10 6 21 14 3 15 } } |
Как работи примерът?
Тази примерна имплементация на двоично дърво не се различава съществено от реализацията, която показахме в случая на обикновено дърво. Отново имаме отделни класове за представяне на двоично дърво и на връх в такова – BinaryTree<T> и BinaryTreeNode<T>. Във вътрешния клас BinaryTreeNode<T> имаме частни полета value и hasParent. Както и преди първото съдържа стойността на върха, а второто показва дали върха има родител. При добавяне на ляв или десен наследник (ляво/дясно дете) на даден връх, се прави проверка дали имат вече родител и ако имат, се хвърля изключение, аналогично на реализацията ни на дърво.
За разлика от реализацията на обикновеното дърво, сега вместо списък на децата, всеки връх съдържа по едно частно поле за ляв и десен наследник. За всеки от тях сме дефинирали публични get и set методи, за да могат да се достъпват от външен за класа код.
В BinaryTree<T> са реализирани три get метода, които връщат съответно корена на дървото, левия му наследник и десния му наследник. Методът traversePreOrder() извиква вътрешно метода preOrder(BinaryTreeNode< T> root). Вторият метод от своя страна обхожда подаденото му дърво по схемата ляво-корен-дясно (ЛКД). Това става по следния тристъпков алгоритъм:
1. Рекурсивно извикване на метода за обхождане за лявото поддърво на дадения връх.
2. Обхождане на самия връх.
3. Рекурсивно извикване на метода за обхождане на дясното поддърво.
Силно препоръчваме на читателя да се опита (като едно добро упражнение) да модифицира предложения алгоритъм и код самостоятелно, така че да реализира другите два основни типа обхождане.
Наредени двоични дървета за претърсване
До момента видяхме как можем да построим обикновено дърво и двоично дърво. Тези структури сами по себе си са доста обобщени и трудно, в такъв суров вид, могат да ни свършат някаква по-сериозна работа. На практика в информатиката се прилагат някои техни разновидности, в които са дефинирани съвкупност от строги правила (алгоритми) за различни операции с тях и с техните елементи. Всяка една от тези разновидности носи със себе си специфични свойства, които са полезни в различни ситуации.
Като примери за такива полезни свойства могат да се дадат бързо търсене на елемент по зададена стойност (червено-черно дърво); нареденост (сортираност) на елементите в дървото; възможност да се организира големи количества информация на някакъв файлов носител, така че търсенето на елемент в него да става бързо с възможно най-малко стъпки (B-дърво) както и много други.
В тази секция ще разгледаме един по-специфичен клас двоични дървета – наредените. Те използват едно често срещано при двоичните дървета свойство на върховете, а именно съществуването на уникален идентификационен ключ във всеки един от тях. Този ключ не се среща никъде другаде в рамките на даденото дърво. Наредените двоични дървета позволяват бързо (в общия случай с приблизително log(n) на брой стъпки) търсене, добавяне и изтриване на елемент, тъй като поддържат елементите си индиректно в сортиран вид.
Сравнимост между обекти
Преди да продължим, ще въведем следната дефиниция, от която ще имаме нужда в по-нататъшното изложение.
Сравнимост – два обекта A и B наричаме сравними, ако е изпълнена точно една от следните три зависимости между тях:
- "A е по-малко от B"
- "A е по-голямо от B"
- "A е равно на B"
Аналогично два ключа A и B ще наричаме сравними, ако е изпълнена точно една от следните три възможности: A < B, A > B или A = B.
Върховете на едно дърво могат да съдържат най-различни полета. В по-нататъшното разсъждение ние ще се интересуваме само от техните уникални ключове, които ще искаме да са сравними. Да покажем един пример. Нека са дадени два конкретни върха A и B:
В примера ключът на A и B са съответно целите числа 19 и 7. Както знаем от математиката, целите числа (за разлика от комплексните например) са сравними, което според гореизложените разсъждения ни дава правото да ги използваме като ключове. Затова за върховете A и B можем да кажем, че "A е по-голямо от B" тъй като "19 е по-голямо от 7".
|
Забележете! Този път числата изобразени във върховете са техни уникални идентификационни ключове, а не както досега произволни числа. |
Стигаме и до дефиницията за наредено двоично дърво за търсене:
Наредено двоично дърво (дърво за търсене, binary search tree) e двоично дърво, в което всеки два от ключовете са сравними и което е организирано, така че за всеки връх да е изпълнено:
- Всички ключове в лявото му поддърво са по-малки от неговия ключ.
- Всички ключове в дясното му поддърво са по-големи от неговия ключ.
Свойства на наредените двоични дървета за претърсване
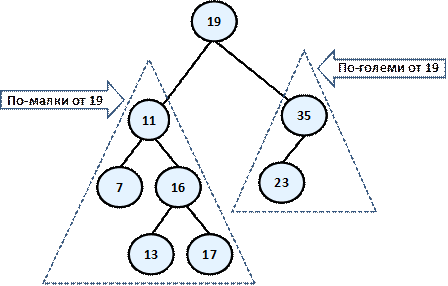
На фигурата е изобразен пример за наредено двоично дърво за претърсване. Ще използваме този пример, за да дадем някой важни свойства на наредеността на двоично дърво:
По дефиниция имаме, че лявото поддърво на всеки един от върховете се състои само от елементи, които са по-малки от него, докато в дясното поддърво има само по-големи елементи. Това означава, че ако искаме да намерим даден елемент тръгвайки от корена, то или сме го намерили или трябва да го търсим съответно в лявото или дясното му поддърво, с което ще спестим излишни сравнения. Например, ако търсим в нашето дърво 23, то няма смисъл да го търсим в лявото поддърво на 19, защото 23 със сигурност не е там (23 е по-голямо от 19 следователно евентуално е в дясното поддърво). Това ни спестява 5 излишни сравнения с всеки един от елементите от лявото поддърво, които, ако използваме свързан списък например, ще трябва да извършим.
От наредеността на елементите следва, че най-малкият елемент в дървото е най-левият наследник на корена, ако има такъв, или самият корен, ако той няма ляв наследник. По абсолютно същия начин най-големият елемент в дървото е най-десният наследник на корена, а ако няма такъв – самият корен. В нашия пример това са минималният елемент 7 и максималният – 35. Полезно и директно следващо свойство от това е, че всеки един елемент от лявото поддърво на даден връх е по-малък от всеки друг, който е в дясното поддърво на същия връх.
Наредени двоични дървета за търсене – пример
Следващият пример показва реализация на двоично дърво за търсене. Целта ни ще бъде да предложим методи за добавяне, търсене и изтриване на елемент в дървото. За всяка една от тези операции ще дадем подробно обяснение как точно се извършва.
Наредени двоични дървета: реализация на върховете
Както и преди, сега ще дефинираме вътрешен клас, който да опише структурата на един връх. По този начин ясно ще разграничим и капсулираме структурата на един връх като същност, която дървото ни ще съдържа в себе си. Този отделен клас сме дефинирали като частен и е видим само в класа на нареденото ни дърво. Ето и неговата дефиниция:
|
... private static class BinaryTreeNode<T extends Comparable<T>> implements Comparable<BinaryTreeNode<T>> { // Contains the value of the node T value;
// Contains the parent of the node BinaryTreeNode<T> parent;
// Contains the left child of the node BinaryTreeNode<T> leftChild;
// Contains the right child of the node BinaryTreeNode<T> rightChild; /** * Constructs the tree node. * @param value – the new value. */ public BinaryTreeNode(T value) { this.value = value; this.parent = null; this.leftChild = null; this.rightChild = null; }
@Override public String toString() { return this.value.toString(); }
@Override public int hashCode() { return this.value.hashCode(); }
@Override public boolean equals(Object obj) { BinaryTreeNode<T> other = (BinaryTreeNode<T>)obj; return this.compareTo(other) == 0; }
public int compareTo(BinaryTreeNode<T> other) { return this.value.compareTo(other.value); } } ... |
Да разгледаме предложения код. Още в името на структурата, която разглеждаме – "наредено дърво за търсене", ние говорим за наредба, а такава можем да постигнем само ако имаме сравнимост между елементите в дървото.
Сравнимост между обекти в Java
Какво означава понятието "сравнимост между обекти" за нас като програмисти? Това означава, че трябва да задължим по някакъв начин всички, които използват нашата структура от данни, да я създават подавайки и тип, който е сравним. На Java изречението "тип, който е сравним" би "звучало" така:
|
T extends Comparable<T> |
Интерфейсът Comparable<T>, намиращ се в пакета java.lang, се състои само от един метод int compareTo(T obj), който връща отрицателно цяло число, нула или положително цяло число съответно, ако текущият обект е по-малък, равен или по-голям от този, който е подаден на метода. Дефиницията му изглежда по приблизително следния начин:
|
public interface Comparable<T> { /** * Compares this object with the specified object for order. * @param obj - the Object to be compared * @return a negative integer, zero, or a positive integer as * this object is less than, equal to, or greater than the * specified object. */ int compareTo(T obj); } |
Имплементирането на този интерфейс от даден клас ни гарантира, че неговите инстанции са сравними.
От друга страна на нас ни е необходимо и самите върхове описани чрез класа BinaryTreeNode също да бъдат сравними помежду си. Затова той също имплементира Comparable<T>. Както се вижда от кода, имплементацията на Comparable<T> на класа BinaryTreeNode вътрешно извиква тази на типа T.
В кода също сме припокрили и методите equals(Object obj) и hashCode(). Добра (задължителна) практика е тези два метода да са съгласувани в поведението си т.е. когато два обекта са еднакви, хеш-кодът им да е еднакъв. Както ще видим в главата за хеш-таблици, обратното въобще не е задължително. Аналогично очакваното поведение на equals(Object obj) е да връща истина, точно когато и compareTo(T obj) връща 0.
|
Задължително синхронизирайте работата на методите equals(Object obj), compareTo(T obj) и hashCode(). Това е тяхното очаквано поведение и ще ви спести много трудно откриваеми проблеми! |
До тук разгледахме методите, предложени от нашият клас. Сега да видим какви полета ни предоставя. Те са съответно за value (ключът) от тип T родител – parent, ляв и десен наследник – съответно leftChild и rightChild. Последните три са от типа на дефиниращия ги клас, а именно BinaryTreeNode.
Наредени двоични дървета: реализация на основния клас
Преминаваме към реализацията на класа, описващ самото наредено двоично дърво. Дървото само по себе си като структура се състои от един корен от тип BinaryTreeNode, който вътрешно съдържа наследниците си – съответно ляв и десен, те вътрешно техните наследници и така рекурсивно надолу докато се стигне до листата. Друго важно за отбелязване нещо е дефиницията BinarySearchTree<T extends Comparable<T>>. Това ограничение на типа T се налага заради изискването на вътрешния ни клас, който работи само с типове, имплементиращи Comparable<T>.
|
public class BinarySearchTree<T extends Comparable<T>> {
/** * Represents a binary tree node. * @author Vesko Kolev * @param <T> */ private static class BinaryTreeNode<T extends Comparable<T>> implements Comparable<BinaryTreeNode<T>> { //... //... The implementation from above goes here!!! ... //... }
/** * The root of the tree. */ private BinaryTreeNode<T> root;
/** * Constructs the tree. */ public BinarySearchTree() { this.root = null; }
//... //... The operation implementation goes here!!! ... //...
} |
Както споменахме по-горе, ще разгледаме следните операции:
- добавяне на елемент;
- търсене на елемент;
- изтриване на елемент.
Добавяне на елемент в подредено двоично дърво
След добавяне на нов елемент, дървото трябва да запази своята нареденост. Алгоритъмът е следният: ако дървото е празно, то добавяме новия елемент като корен. В противен случай:
- Ако елементът е по-малък от корена, то се обръщаме рекурсивно към същия метод, за да включим елемента в лявото поддърво.
- Ако елементът е по-голям от корена, то се обръщаме рекурсивно към същия метод, за да включим елемента в дясното поддърво.
- Ако елементът е равен на корена, то не правим нищо и излизаме от рекурсията.
Ясно се вижда как алгоритъмът за включване на връх изрично се съобразява с правилото елементите в лявото поддърво да са по-малки от корена на дървото и елементите от дясното поддърво да са по-големи от корена на дървото. Ето и примерна имплементация на този метод. Забележете, че при включването се поддържа референция към родителя, защото родителят също трябва да бъде променен.
|
/** * Inserts new value in the binary search tree. * @param value - the value to be inserted. */ public void insert(T value) { if (value == null) { throw new IllegalArgumentException(); }
this.root = insert(value, null, root); }
/** * Inserts node in the binary search tree by given value. * @param value - the new value. * @param parentNode - the parent of the new node. * @param node - current node. * @return the inserted node */ private BinaryTreeNode<T> insert(T value, BinaryTreeNode<T> parentNode, BinaryTreeNode<T> node) { if (node == null) { node = new BinaryTreeNode<T>(value); node.parent = parentNode; } else { int compareTo = value.compareTo(node.value); if (compareTo < 0) { node.leftChild = insert(value, node, node.leftChild); } else if (compareTo > 0) { node.rightChild = insert(value, node, node.rightChild); } }
return node; } |
Търсене на елемент в подредено двоично дърво
Търсенето е операция, която е още по-интуитивна. В примерния код сме показали как може търсенето да се извърши без рекурсия, чрез итерация. Алгоритъмът започва с елемент node, сочещ корена. След това се прави следното:
- Ако елементът е равен на node, то сме намерили търсения елемент и го връщаме.
- Ако елементът е по-малък от node, то присвояваме на node левия му наследник т.е. продължаваме търсенето в лявото поддърво.
- Ако елементът е по-голям от node, то присвояваме на node десния му наследник т.е. продължаваме търсенето в дясното поддърво.
Следва примерен код:
|
/** * Finds a given value in the tree and returns the node * which contains it if such exsists. * @param value - the value to be found. * @return the found node or null if not found. */ private BinaryTreeNode<T> find(T value) { BinaryTreeNode<T> node = this.root;
while (node != null) { int compareTo = value.compareTo(node.value); if (compareTo < 0) { node = node.leftChild; } else if (compareTo > 0) { node = node.rightChild; } else { break; } }
return node; } |
Изтриване на елемент от подредено двоично дърво
Изтриването е най-сложната операция от трите основни. След нея дървото трябва да запази своята нареденост. Първата стъпка преди да изтрием елемент от дървото е да го намерим. Вече знаем как става това. След това се прави следното:
- Ако върхът е листо – насочваме референцията на родителя му към null. Ако елементът няма родител следва, че той е корен и просто го изтриваме.
- Ако върхът има само едно поддърво – ляво или дясно, то той се замества с корена на това поддърво.
- Ако върхът има две поддървета. Тогава намираме най-малкият връх в дясното му поддърво и го разменяме с него. След тази размяна върхът ще има вече най-много едно поддърво и го изтриваме по някое от горните две правила. Тук трябва да отбележим, че може да се направи аналогична размяна, само че взимаме лявото поддърво и най-големият елемент от него.
Оставяме на читателя като леко упражнение да провери коректността на всяка от тези три стъпки.
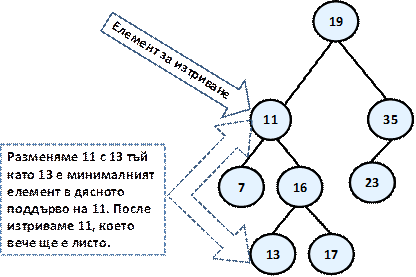
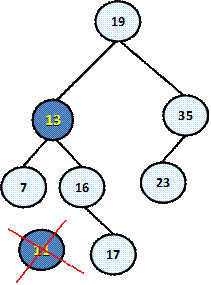
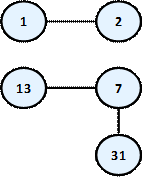
Нека даден един пример за изтриване. Ще използваме отново нашето наредено дърво, което показахме в началото на тази точка. Да изтрием например елемента с ключ 11.
Той има две поддървета и съгласно нашият алгоритъм трябва да бъде разменен с най-малкият елемент от дясното поддърво, т.е. с 13. След като извършим размяната вече можем спокойно да изтрием 11, който е листо. Ето крайният резултат:
Предлагаме следния примерен код, който реализира описания алгоритъм:
|
/** * Removes an element from the tree if exists. * @param value - the value to be deleted. */ public void remove(T value) { BinaryTreeNode<T> nodeToDelete = find(value); if (nodeToDelete == null) { return; }
remove(nodeToDelete); }
public void remove(BinaryTreeNode<T> node) { // Case 3: If the node has two children. // Note that if we get here at the end // the node will be with at most one child. if (node.leftChild != null && node.rightChild != null) { BinaryTreeNode<T> replacement = node.rightChild; while (replacement.leftChild != null) { replacement = replacement.leftChild; } node.value = replacement.value; node = replacement; }
// Case 1 and 2: If the node has at most one child. BinaryTreeNode<T> theChild = node.leftChild != null ? node.leftChild : node.rightChild;
// If the element to be deleted has one child. if (theChild != null) { theChild.parent = node.parent;
// Handle the case when the element is the root. if (node.parent == null) { root = theChild; } else { // Replace the element with its child subtree. if (node.parent.leftChild == node) { node.parent.leftChild = theChild; } else { node.parent.rightChild = theChild; } } } else { // Handle the case when the element is the root. if (node.parent == null) { root = null; } else { // Remove the element. It is a leaf. if (node.parent.leftChild == node) { node.parent.leftChild = null; } else { node.parent.rightChild = null; } } } } |
Балансирани дървета
Както видяхме по-горе, наредените двоични дървета представляват една много удобна структура за търсене. Така дефинирани операциите за създаване и изтриване на дървото имат един скрит недостатък. Какво би станало ако в дървото включим последователно елементите 1, 2, 3, 4, 5, 6? Ще се получи следното дърво:
В този случай двоичното дърво се е изродило в свързан списък. От там и търсенето в това дърво ще е доста по-бавно (с N на брой стъпки, а не с log(N)), тъй като, за да проверим дали даден елемент е вътре, в най-лошият случай ще трябва да преминем през всички елементи.
Ще споменем накратко за съществуването на структури от данни, които в общия случай запазват логаритмичното поведение на операциите добавяне, търсене и изтриване на елемент. Преди да кажем как се постига това, ще въведем следните две дефиниции:
Балансирано двоично дърво – двоично дърво, в което никое листо не е на "много по-голяма" дълбочина от всяко друго листо. Дефиницията на "много по-голяма" зависи от конкретната балансираща схема.
Идеално балансирано двоично дърво – двоично дърво, в което разликата в броя на върховете на лявото и дясното поддърво на всеки от върховете е най-много единица.
Без да навлизаме в детайли ще споменем, че ако дадено двоично дърво е балансирано, дори и да не е идеално балансирано, то операциите за добавяне, търсене и изтриване на елемент в него са с логаритмична сложност и дори и в най-лошия случай. За да се избегне дисбаланса на дървото за претърсване, се прилагат операции, които пренареждат част от елементите на дървото при добавяне или при премахване на елемент от него. Тези операции най-често се наричат ротации. Конкретният вид на ротациите, се уточнява допълнително и зависи реализацията от конкретната структура от данни. Като примери за такива структури, можем да дадем червено-черно дърво, AVL-дърво, AA-дърво, Splay-дърво и др.
За по-детайлно разглеждане на тези и други структури препоръчваме на читателя да потърси в строго специализираната литература за алгоритми и структури от данни.
Класът TreeSet<T> в Java
След като вече се запознахме с наредените двоични дървета и с това какво е предимството те да са балансирани, идва момента да покажем и какво Java има за нас по този въпрос. Може би всеки от вас тайно се е надявал, че никога няма да му се налага да имплементира балансирано наредено двоично дърво за търсене, защото изглежда доста сложно. Това най-вероятно наистина е така.
До момента разгледахме какво представляват балансираните дървета, за да добиете представа за тях. Когато ви се наложи да ги ползвате, винаги можете да разчитате да ги вземете от някъде наготово. В стандартните библиотеки на Java има готови имплементации на балансирани дървета, а освен това по Интернет можете да намерите и много външни библиотеки, като примерно Apache Commons Collections и JGL.
В Java Collection Framework се поддържа класът TreeSet<T>, който вътрешно представлява имплементация на червено-черно дърво. Това, както вече знаем, означава, че добавянето, търсенето и изтриването на елементи в дървото ще се извърши с логаритмична сложност (т.е. ако имаме 1 000 000 елемента операцията ще бъде извършена за около 20 стъпки). Методите са съответно с имена add(), contains() и remove().
Важно е да се отбележи, че итераторът на TreeSet<T> ще връща елементите на дървото един по един в нарастващ ред, като се започне от най-малкия. Това се дължи на вътрешната наредба на елементите. Следва да отбележим, че итераторите са класове, които се използват за обхождане на дадена колекция. Има случаи, в които се имплементират повече от един итератори, за да могат да бъдат постигнати няколко различни обхождания на дадената структура.
Класът TreeSet<T> – пример
Ето прост пример, който показва, че в TreeSet<T> можем да добавяме и изтриваме, а при обхождане получаваме елементите в нарастващ ред:
|
TreeSet<Integer> treeSet = new TreeSet<Integer>(); treeSet.add(5); treeSet.add(8); treeSet.add(1); treeSet.add(6); treeSet.add(3); treeSet.remove(6); for (int i : treeSet) { System.out.printf(" %d", i); } // Result: 1 3 5 8 |
Повече информация за класа TreeSet<T> можете да намерите в секцията "Множества" на главата "Речници, хеш-таблици и множества".
Графи
Графите се една изключително полезна и доста разпространена структура от данни. Използват се за описването на най-разнообразни взаимовръзки между обекти от практиката, свързани с почти всичко. Както ще видим по-късно, дървета са подмножество на графите, т.е. графите представляват една обобщена структура, позволяваща моделирането на доста голяма съвкупност от реални ситуации.
Честата употреба на графите в практиката е довела до задълбочени изследвания в "теория на графите", в която са известни огромен брой задачи за графи и за повечето от тях има и добре известно решение.
Графи – основни понятия
В тази точка ще въведем някои от по-важните понятия и дефиниции. Част от тях са аналогични на тези, въведени при структурата от данни дърво, но двете структури, както ще видим, имат много сериозни различия, тъй като дървото е само един частен случай на граф.
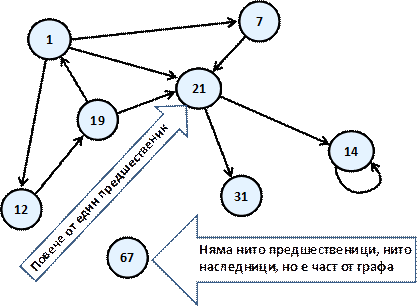
Да разгледаме следният примерен граф, чийто тип по-късно ще наречем краен ориентиран. В него отново имаме номерация на върховете, която е абсолютно произволна и е добавена, за да може по-лесно да говорим за някой конкретен:
Кръгчетата на схемата, ще наричаме върхове, а стрелките, които ги свързват, ще наричаме ориентирани ребра (дъги). Върхът, от който излиза стрелката ще наричаме предшественик на този, който стрелката сочи. Например "19" е предшественик на "1". "1" от своя страна се явява наследник на "19". За разлика от структурата дърво, сега всеки един връх може да има повече от един предшественик. Например "21" има трима - "19", "1" и "7". Ако два върха са свързани с ребро, то казваме, че тези два върха са инцидентни с това ребро.
Следва дефиниция за краен ориентиран граф (finite directed graph):
Краен ориентиран граф се нарича наредената двойката двойка (V, E), където V е крайно множество от върхове, а E е крайно множество от ориентирани ребра. Всяко ребро е принадлежащо на E представлява наредена двойка от върхове u и v т.е. e=(u, v), които еднозначно го определят.
За по-доброто разбиране на тази дефиниция силно препоръчваме на читателя да си мисли за върховете например като за градове, а ориентираните ребра като еднопосочни пътища. Така, ако единият връх е София, а другият е Велико Търново то еднопосочният път (дъгата) ще се нарича София-Велико Търново. Всъщност това е един от класическите примери за приложение на графите – в задачи свързани с пътища.
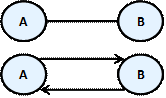
Ако вместо стрелки върховете са свързани с отсечки (както при структурата дърво), то тогава отсечките ще наричаме неориентирани ребра, а графът – неориентиран. На практика можем да си представяме, че едно неориентирано ребро от връх A до връх B представлява двупосочно ребро еквивалентно на две противоположни ориентирани ребра между същите два върха:
Два върха свързани с ребро, ще наричаме съседни.
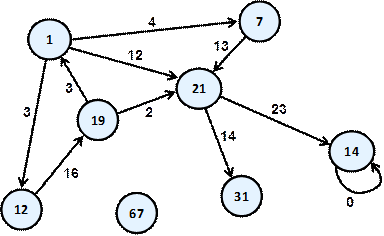
За ребрата може се зададе функция, която на всяко едно ребро съпоставя реално число. Тези така получени реални числа ще наричаме тегла. Като примери за тегла можем да дадем дължината на директните връзки между два съседни града, пропускателната способност на една тръба и др. Граф, който има тегла по ребрата се нарича претеглен (weighted). Ето как се изобразява претеглен граф:
Път в граф ще наричаме последователност от върхове v1, v2, … , vn, такава, че съществува ребро от vi до vi+1 за всяко i от 1 до n-1. В нашия граф път е например последователността "1", "12", "19", "21". "7", "21" и "1" обаче не е път, тъй като не съществува ребро започващо от "21" и завършващо в "1".
Дължина на път е броят на ребрата, свързващи последователността от върхове в пътя. Този брой е равен на броят на върховете в пътя минус единица. Дължината на примера ни за път "1", "12", "19", "21" е три.
Цена на път в претеглен граф, ще наричаме сумата от теглата на ребрата участващи в пътя. В реалния живот пътят от София до Варна например е равен на дължината на пътя от София до Велико Търново плюс дължината на пътя от Велико Търново до Варна. В нашия пример дължината на пътя "1", "12", "19" и "21" е равна на 3 + 16 + 2 = 21.
Цикъл е път, в който началният и крайният връх на пътя съвпадат. Пример за цикъл е "1", "12" и "19". "1", "7" и "21" обаче не е цикъл.
Примка ще наричаме ребро, което започва от и свършва в един и същ връх. В нашия пример върха "14" има примка.
Свързан неориентиран граф наричаме неориентиран граф, в който съществува път от всеки един връх до всеки друг. Например следният граф не е свързан, защото не съществува път от "1" до "7".
И така, вече имаме достатъчно познания, за да дефинираме понятието дърво по още един начин – като специален вид граф:
Дърво – неориентиран свързан граф без цикли.
Като леко упражнение оставяме на читателя да покаже защо двете дефиниции за дърво са еквивалентни.
Графи – видове представяния
Съществуват много различни начини за представяне на граф в програмирането. Различните представяния имат различни свойства и кое точно трябва да бъде избрано, зависи от конкретния алгоритъм, който искаме да приложим. С други думи казано – представяме графа си така, че операциите, които алгоритъмът ни най-често извършва върху него, да бъдат максимално бързи. Без да изпадаме в големи детайли ще изложим някои от най-често срещаните представяния на графи.
- Списък на ребрата – представя се, чрез списък от наредени двойки (vi, vj), където съществува ребро от vi до vj. Ако графът е претеглен, то вместо наредена двойка имаме наредена тройка, като третият й елемент показва какво е теглото на даденото ребро.
- Списък на наследниците – в това представяне за всеки връх v се пази списък с върховете, към които сочат ребрата започващи от v. Тук отново, ако графът е претеглен, към всеки елемент от списъка с наследниците се добавя допълнително поле, показващо цената на реброто до него.
- Матрица на съседство – графът се представя като квадратна матрица g[N][N], в която, ако съществува ребро от vi до vj, то на позиция g[i][j] в матрицата е записано 1. Ако такова ребро не съществува, то в полето g[i][j] е записано 0. Ако графът е претеглен, в позиция g[i][j] се записва теглото на даденото ребро, а матрицата се нарича матрица на теглата. Ако между два върха в такава матрица не съществува път, то тогава се записва специална стойност, означаваща безкрайност.
- Матрица на инцидентност между върхове и ребра – в този случай отново се използва матрица, само че с размери g[M][N], където М е броят на върховете, а N е броят на ребрата. Всеки стълб представя едно ребро, а всеки ред един връх. Тогава в стълба съответстващ на реброто (vi, vj) само и единствено на позиция i и на позиция j ще бъдат записани 1, а на останалите позиции в този стълб ще е записана 0. Ако реброто е примка т.е. е (vi, vi), то на позиция i записваме 2. Ако графът, който искаме да представим е ориентиран и искаме да представим ребро от vi до vj, то на позиция i пишем 1, а на позиция j пишем -1.
Графи – основни операции
Основните операции в граф са:
- Създаване на граф
- Добавяне / премахване на връх / ребро
- Проверка дали даден връх / ребро съществува
- Намиране на наследниците на даден връх
Ще предложим примерна реализация на представяне на граф с матрица на съседство и ще покажем как се извършват повечето операции. Този вид реализация е удобен, когато максималният брой на върховете е предварително известен и когато той не е много голям (за да се реализира представянето на граф с N върха е необходима памет от порядъка на N2 заради квадратната матрица). Поради това, няма да реализираме методи за добавяне / премахване на нов връх.
|
import java.util.LinkedList; import java.util.List;
/** * Represents a directed unweighted graph structure. * @author Vesko Kolev */ public class Graph { // Contains the vertices of the graph private int vertices[][];
/** * Constructs the graph. * @param vertices - the vertices of the graph. */ public Graph(int[][] vertices) { this.vertices = vertices; }
/** * Adds new edge from i to j. * @param i - the starting vertex. * @param j - the ending vertex. */ public void addEdge(int i, int j) { vertices[i][j] = 1; }
/** * Removes the edge from i to j if such exists. * @param i - the starting vertex. * @param j - the ending vertex. */ public void removeEdge(int i, int j) { vertices[i][j] = 0; }
/** * Checks whether there is an edge between vertex i and j. * @param i - the starting vertex. * @param j - the ending vertex. * @return true if there is an edge between * vertex i and vertex j. */ public boolean hasEdge(int i, int j) { return vertices[i][j] == 1; }
/** * Returns the successors of a given vertex. * @param i - the vertex. * @return list with all successors of the given vertex. */ public List<Integer> getSuccessors(int i) { List<Integer> successors = new LinkedList<Integer>();
for (int j = 0; j < vertices[i].length; i++) { if (vertices[i][j] == 1) { successors.add(j); } }
return successors; } } |
Основни приложения и задачи за графи
Графите се използват за моделиране на много ситуации от реалността, а задачите върху графи моделират множество реални проблеми, които често се налага да бъдат решавани. Ще дадем само няколко примера:
- Карта на град може да се моделира с ориентиран претеглен граф. На всяка улица се съпоставя ребро с дължина съответстваща на дължината на улицата и посока – посоката на движение. Ако улицата е двупосочна може да й се съпоставят две ребра за двете посоки на движение. На всяко кръстовище се съпоставя връх. При такъв модел са естествени задачи като търсене на най-кратък път между две кръстовища, проверка дали има път между две кръстовища, проверка за цикъл (дали можем да се завъртим и да се върнем на изходна позиция), търсене на път с минимален брой завои и т.н.
- Компютърна мрежа може да се моделира с неориентиран граф, чиито върхове съответстват на компютрите в мрежата, а ребрата съответстват на комуникационните канали между компютрите. На ребрата могат да се съпоставят различни числа, примерно капацитет на канала или скорост на обмена и др. Типични задачи при такива модели на компютърна мрежа са проверка за свързаност между два компютъра, проверка за двусвързаност между две точки (съществуване на двойно-подсигурен канал, който остава при отказ на който и да е компютър) и др. В частност Интернет може да се моделира като граф, в който се решават задачи за маршрутизация на пакети, които се моделират като задачи за графи.
- Речната система в даден регион може да се моделира с насочен претеглен граф, в който всяка река се състои от едно или няколко ребра, а всеки връх съответства на място, където две или повече реки се вливат една в друга. По ребрата могат да се съпоставят стойности, свързани с количеството вода, което преминава по тях. Естествени при този модел са задачи като изчисление на обемите вода, преминаващи през всеки връх и предвиждане на евентуални наводнения при увеличаване на количествата.
Виждате, че графите могат да имат многобройни приложения. За тях има изписани стотици книги и научни трудове. Съществуват десетки класически задачи за графи, за които има известни решения или е известно, че нямат ефективно решение. Ние няма да се спираме на тях. Надяваме се чрез краткото представяне да събудим интересът ви към темата и да ви подтикнем да отделите достатъчно внимание на задачите за графи от упражненията.
Упражнения
1. Да се напише програма, която намира броя на срещанията на дадено число в дадено дърво от числа.
2. Да се напише програма, която извежда корените на онези поддървета на дадено дърво, които имат точно k на брой върха, където k e дадено естествено число.
3. Да се напише програма, която намира броя на листата и броя на вътрешните върхове на дадено дърво.
4. Напишете програма, която по дадено двоично дърво от числа намира сумата на върховете от всяко едно ниво на дървото.
5. Да се напише програма, която намира и отпечатва всички върхове на двоично дърво, които имат за наследници само листа.
6. Да се напише програма, която проверява дали дадено двоично дърво е идеално балансирано.
7. Нека е даден граф G(V, E) и два негови върха x и y. Напишете програма, която намира най-краткия път между два върха по брой на върховете.
8. Нека е даден граф G(V, E). Напишете програма, която проверява дали графът е цикличен.
9. Нека е даден граф G(V, E). Напишете програма, която намира всички компоненти на свързаност на графа, т.е. намира всички негови максимални свързани подграфи. Максимален свързан подграф на G е свързан граф такъв, че няма друг подграф на G, който да е свързан и да го съдържа.
10. Нека е даден претеглен ориентиран граф G(V, E), в който теглата по ребрата са неотрицателни числа. Напишете програма, която по зададен връх x от графа намира минималните пътища от него до всички останали.
11. Имаме N задачи, които трябва да бъдат изпълнени последователно. Даден е списък с двойки задачи, за които втората зависи от резултата от първата и трябва да бъде изпълнена след нея. Напишете програма, която подрежда задачите по такъв начин, че всяка задача да се изпълни след всички задачи, от които зависи. Ако не съществува такава наредба, да се отпечата подходящо съобщение.
12. Ойлеров цикъл в граф се нарича цикъл, който започва от даден връх, минава точно по веднъж през всички негови ребра и се връща в началния връх. При това обхождане всеки връх може да бъде посетен многократно. Напишете програма, която по даден граф намира в него Ойлеров цикъл или установява, че такъв няма.
13. Хамилтонов цикъл в граф се нарича цикъл, съдържащ всеки връх в графа точно по веднъж. Да се напише програма, която при даден претеглен ориентиран граф G(V, E), намира Хамилтонов цикъл с минимална дължина, ако такъв съществува.
Решения и упътвания
1. Обходете рекурсивно дървото в дълбочина и пребройте срещанията на даденото число.
2. Обходете рекурсивно дървото в дълбочина и проверете за всеки връх даденото условие.
3. Можете да решите задачата с рекурсивно обхождане на дървото в дълбочина.
4. Използвайте обхождане в дълбочина или в ширина и при преминаване от един връх в друг запазвайте в него на кое ниво се намира. Знаейки нивата на върховете търсената сума лесно се изчислява.
5. Можете да решите задачата с рекурсивно обхождане на дървото в дълбочина и проверка на даденото условие.
6. Чрез рекурсивно спускане в дълбочина за всеки връх на дървото изчислете дълбочините на лявото и дясното му поддърво. След това проверете непосредствено дали е изпълнено условието от дефиницията за идеално балансирано дърво.
7. Използвайте като основа алгоритъма за обхождане в ширина. Слагайте в опашката заедно с даден връх и неговия предшественик. Това ще ви помогне накрая да възстановите пътя между върховете (в обратен ред).
8. Използвайте обхождане в дълбочина или в ширина. Отбелязвайте за всеки връх дали вече е бил посетен. Ако в даден момент достигнете до връх, който е бил посетен по-рано, значи сте намерили цикъл.
Помислете как можете да намерите и отпечатате самия цикъл. Ето една възможна идея: при обхождане в дълбочина за всеки връх пазите предшественика му. Ако в даден момент стигнете до връх, който вече е бил посетен, вие би трябвало да имате запазен за него някакъв път до началния връх. Текущият път в стека на рекурсията също е път до въпросния връх. Така в даден момент имаме два различни пътя от един връх до началния връх. От двата пътя лесно можете да намерите цикъл.
9. Използвайте като основа алгоритъма за обхождане в ширина или в дълбочина.
10. Използвайте алгоритъма на Dijkstra (намерете го в Интернет).
11. Търсената наредба се нарича "топологично сортиране на ориентиран граф". Може да се реализира по два начина:
За всяка задача t пазим от колко на брой други задачи P(t) зависи. Намираме задача t0, която не зависи от никоя друга (P(t0)=0) и я изпълняваме. Намаляваме P(t) за всяка задача t, която зависи от t0. Отново търсим задача, която не зависи от никоя друга и я изпълняваме. Повтаряме докато задачите свършат или до момент, в който няма нито една задача tk с P(tk)=0.
Можем да решим задачата чрез обхождане в дълбочина на графа и печатане на всеки връх при напускането му. Това означава, че в момента на отпечатването на дадена задача всички задачи, които зависят от нея са били вече отпечатани.
12. За да съществува Ойлеров цикъл в даден граф, трябва графът да е свързан и степента на всеки негов връх да е четно число. Чрез поредица впускания в дълбочина можете да намирате цикли в графа и да премахвате ребрата, които участват в тях. Накрая като съедините циклите един с друг ще получите Ойлеров цикъл.
13. Ако напишете вярно решение на задачата, проверете дали работи за граф с 200 върха. Не се опитвайте да решите задачата, така че да работи бързо за голям брой върхове. Ако някой успее да я реши, ще остане трайно в историята!
Дискусионен форум
Коментирайте книгата и задачите в нея във: форума на софтуерната академия.
Тагове: BFS, DFS, Java, Java книга, балансирани дървета, графи, двоични дървета, дървета, дървовидни структури данни, книга, обхождане в дълбочина, обхождане в ширина, търсене в дълбочина, търсене в ширина5 отговора до “Глава 17. Дървета и графи”
Коментирай
Трябва да сте влезнали, за да коментирате.

Breath-First-Search – какво точно имате предвид?
И в трите книги е така (Java, C#, C# engl.)
Breath – дъх, дихание, дишане
или
Breadth – ширина, широчина
Трябва да е ширина, как не сме го забелязали….
Поправих го, но е сбъркано на много места.
Понеже няма пояснение след посочения пример, искам да попитам дали е грешка или така трябва да бъде?
В частта с Графи – основни операции е даден метода
public List getSuccessors(int i) {
List successors = new LinkedList();
for (int j = 0; j < vertices[i].length; i++) {
if (vertices[i][j] == 1) {
successors.add(j);
}
}
return successors;
}
Питането ми конкретно е за For цикъла. в началото е даден j=0, но после се дава i++
дали е грешка или така трябва да си е и ако да защо?
Трябва да е j++ , защото това е матрица за съседство и трябва да обходиш колоните на матрицата за дадения като параметър ред.
По-добре питай във форума: https://softuni.bg/forum