Chapter 26. Sample Programming Exam – Topic #3
In the present chapter we will review some sample exam problems and suggest solutions for them. While solving the problems we will stick to the advices given in the chapter "Methodology of Problem Solving".
Content
- Mind Maps
- In This Chapter
- Problem 1: Spiral Matrix
- Problem 2: Counting Words in a Text File
- Problem 3: School
- Exercises
- Solutions and Guidelines
- Discussion Forum
Mind Maps
With a given number N (input from the keyboard) generate and print a square matrix containing the numbers from 0 to N2-1, located as a spiral beginning from the center of the matrix and moving clockwise starting downwards (look at the examples).
Sample output for N=3 and N=4:
Start Thinking on the Problem
It’s obvious from the requirement that we are given an algorithmic problem. Contriving the appropriate algorithm for filling up the square matrix cells in the required way is the main part of the solution to the problem. We will demonstrate to the reader the typical reasoning needed for solving this particular problem.
Inventing an Idea for the Solution
The next step is to think up the idea for the algorithm, which we will implement. We must fill the matrix with the numbers from 0 to N2-1 and we may immediately notice that this could be made by a loop, which puts one of the numbers in the supposed cell of the matrix at each iteration. We first put 0 at its place, then put 1 at its place, then put 2, and so on until we finish with putting N2-1 at its place.
Let’s suppose we know the starting position – the one we have to put the first number on (the zero). That’s how the problem is reduced to finding a method for determining each of the next positions, which we must put a number at – this is our primary subtask.
We try to find an approach for determining the next to the current position: we search a strict regularity for changing the indices during the traversal of the cells. It looks like the directions of the numbers are changed from time to time, right? First the direction if down, then the direction is changed to left, later to up, then to right then again to down. Changing of the directions is always clockwise and the initial direction is always downwards.
If we define an integer variable direction that holds the current moving direction, it will take sequentially the values 0 (down), 1 (left), 2 (up), 3 (right) and then again 0, 1, 2, … Looking at the problem examples (for N=3 and N=4) we can conclude that the direction stays down for some time, then changes to left, stays some time, then changes to up, stays some time, etc. We can assume that with changing the moving direction we can increase the value of direction by one and take its remainder of division by 4. Thus the next direction after 3 (right) will be 0 (down).
The next step is to determine when the moving direction changes: what is the number of moves in each direction. This may take some time. We can take a sheet of paper and test few hypotheses we might have.
From the two examples we can see that the number of moves in the consequent directions does form special sequences: for N=3 à 1, 1, 2, 2, 2 and for N=4 à 1, 1, 2, 2, 3, 3, 3. This means that for N=3 we move 1 cell down, then 1 cell left, then 2 cells up, then 2 cells right and finally 2 down. For N=4, the process is the same. We found an interesting dependency which can evolve into an algorithm for filling the spiral matrix.
If we write down a bigger matrix of the same type on a sheet of paper, we will see that the sequence of the changes of direction follows the same pattern: the numbers increases by 1 at an interval of two and the last number does not increase.
Seems like we have an idea to solve the problem: start from the middle of the matrix and move 1 cell down, 1 cell left, 2 cells up, 2 cells right, 3 cells down, 3 cells left, etc. During the moving we can fill the numbers from 0 to N2-1 consequently at the cells we visit.
Checking the Idea
Let’s check the idea. First we need to find the starting cell and check we have a correct algorithm for it. If N is odd, the starting cell seems to be the absolute center cell of the matrix. We can check this for N=1, N=3 and N=5 on a sheet of paper and this confirms to be correct. If N is even number, it seems like the starting cell is located upper-right from the central point of the matrix. At the figure below the central point is shown for a matrix of size 4 x 4 and the starting point located at the upper-right direction:
Now let’s check the matrix filling algorithm. We take for example N=4. Let’s start from the starting cell. The first direction is down. We go down 1 cell, then left 1 cell, then up 2 cells, then right 2 cells, then down 3 cells, then left 3 cells and finally up 3 cells. For simplicity we can assume the last step is 4 cells up but we stop at the first moment when the entire matrix if filled. The figure below shows what we could draw on a sheet of paper to trace how the algorithm works. See the small sketch of our algorithm, done by hand during the idea checking process:
After sketching the algorithm paper for N = 1, 2 and 3 on a sheet of paper we see that it works correctly. Seems like the idea is correct and we can thinks about how to implement it.
Data Structures and Efficiency
Let’s start with choosing the data structure for implementing the matrix. It’s appropriate to have direct access to each element of the matrix so we will choose a two-dimensional array matrix of integer type. When starting the program we read from the standard input the dimensionality n of the matrix and initialize it as it follows:
|
int[,] matrix = new int[n,n]; |
In this case the choice of a data structure is unambiguous. We will keep the matrix in a two-dimensional array. We have no other data. We will not have problems with the performance because the program will make as much steps as the elements in the matrix are.
Implementation of the Idea: Step by Step
We may split the implementation into few steps. A loop runs from 0 to N2-1 and at each iteration it does the following steps:
- Fill the current cell of the matrix with the next number (this is a single move in the current direction).
- Check whether the current direction should be changed and if yes, change it and calculate the number of moves in the new direction.
- Move the current position to the next cell in the current direction (e.g. one position down / left / up / right).
Implementing the First Few Steps
We can represent the current position with integer variables positionX and positionY – the two coordinates for the position. At each iteration we will move to the next cell in the current direction and positionX and positionX will change accordingly.
For modeling the behavior of filling the spiral matrix we will use the variables stepsCount (total number of moves in the current direction), stepPosition (the move number in the current direction) and stepChange (flag showing if we have to change the value of stepCount – increments after every 2 direction changes).
Let’s see how we can implement this idea as a code:
|
for (int i = 0; i < count; i++) { // Fill the current cell with the current value matrix[positionY, positionX] = i;
// Check for direction / step changes if (stepPosition < stepsCount) { stepPosition++; } else { stepPosition = 1; if (stepChange == 1) { stepsCount++; } stepChange = (stepChange + 1) % 2; direction = (direction + 1) % 4; }
// Move to the next cell in the current direction switch (direction) { case 0: positionY++; break; case 1: positionX--; break; case 2: positionY--; break; case 3: positionX++; break; } } |
Performing a Partial Check after the First Few Steps
This is the moment to point out the unlikelihood of creating the body of such a loop from the first time, without making any mistakes. We already know the rule for writing the code step by step and testing after each piece of code is written but for the body of this loop the rule is hard to be applied – we have no independent subproblems, which can be tested separately of each other. To test the above code we need first to finish it: to assign initial values for all the variables used.
Assigning the Initial Values
After we have a well thought-out idea for the algorithm (even if we are not completely sure that the written code will work correctly), it remains to set initial values of the already defined variables and to print the matrix, obtained after the implementation of the loop.
It is clear that the number of loop iterations is exactly N2 and that’s why we replace the variable count with this value. From the two given examples and our own additional examples (written on a paper) we determine the initial position in the matrix depending on the parity (odd / even) of its size:
|
int positionX = n / 2; // The middle of the matrix int positionY = n % 2 == 0 ? (n / 2) - 1 : (n / 2); // middle |
To the rest of the variables we give the following initial values (we have already explained their semantics):
|
int direction = 0; // The initial direction is "down" int stepsCount = 1; // Perform 1 step in the current direction int stepPosition = 0; // 0 steps already performed int stepChange = 0; // Steps count will change after 2 steps |
Putting All Together
The last subproblem we have to solve for creating a working program is printing the matrix on the standard output. Let’s write it, then put all code together and start testing.
The fully implemented solution is shown below. It includes reading the input data (matrix size), filling the matrix in a spiral (calculating the matrix center and filling it cell by cell) and output the result:
|
MatrixSpiral.cs |
|
using System;
public class MatrixSpiral { static void Main() { Console.Write("N = "); int n = int.Parse(Console.ReadLine()); int[,] matrix = new int[n, n];
FillMatrix(matrix, n);
PrintMatrix(matrix, n); }
private static void FillMatrix(int[,] matrix, int n) { int positionX = n / 2; // The middle of the matrix int positionY = n % 2 == 0 ? (n / 2) - 1 : (n / 2);
int direction = 0; // The initial direction is "down" int stepsCount = 1; // Perform 1 step in current direction int stepPosition = 0; // 0 steps already performed int stepChange = 0; // Steps count changes after 2 steps
for (int i = 0; i < n * n; i++) { // Fill the current cell with the current value matrix[positionY, positionX] = i;
// Check for direction / step changes if (stepPosition < stepsCount) { stepPosition++; } else { stepPosition = 1; if (stepChange == 1) { stepsCount++; } stepChange = (stepChange + 1) % 2; direction = (direction + 1) % 4; }
// Move to the next cell in the current direction switch (direction) { case 0: positionY++; break; case 1: positionX--; break; case 2: positionY--; break; case 3: positionX++; break; } } }
private static void PrintMatrix(int[,] matrix, int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { Console.Write("{0,3}", matrix[i, j]); } Console.WriteLine(); } } } |
Testing the Solution
After we have implemented the solution it is appropriate to test it with enough values of N to ensure it works properly. We start with the sample values 3 and 4 and then we check for 5, 6, 7, 8, 9, … It works well.
It is important to check the border cases: 0 and 1. They work correctly as well. We do few more tests and we make sure all cases work correctly. We might notice that when N is large (e.g. 50) the output looks ugly, but this cannot be improved much. We can add more spaces between the numbers but the console is limited to 80 characters and the result is still ugly. We will not try to improve this further.
It is not necessary to test the program for speed (performance test, for example with N=1,000) because with a very big N the output will be extremely large and the task will be pointless.
We cannot find any non-working cases so we assume the algorithm and its implementation are both correct and the problem is successfully solved.
Now we are ready for the next problem from the exam.
Problem 2: Counting Words in a Text File
We are given a text file words.txt, which contains several words, one per each line. Each word consists of Latin letters only. Write a program, which retrieves the number of matches of each of the given words as a substring in the file text.txt. The counting is case insensitive. The result should be written into a text file named result.txt in the following format (the words should appear in the same order as given in the input file words.txt):
|
<word1> --> <number of matches> <word2> --> <number of matches> … |
Sample input file words.txt:
|
for academy student Java develop CAD |
Sample input file text.txt:
|
The Telerik Academy for software development engineers is a famous center for free professional training of .NET experts. Telerik Academy offers courses designed to develop practical computer programming skills. Students graduated the Academy are guaranteed to have a job as a software developers in Telerik. |
Sample result file result.txt:
|
for --> 2 academy --> 3 student --> 1 Java --> 0 develop --> 3 CAD --> 3 |
Below are the locations of the matched words from the above example:
|
The Telerik Academy for software development engineers is a famous center for free professional training of .NET experts. Telerik Academy offers courses designed to develop practical computer programming skills. Students graduated the Academy are guaranteed to have a job as a software developers in Telerik. |
Start Thinking on the Problem
The emphasis of the given problem seems not so much on the algorithm, but on its technical implementation. In order to write the solution we must be familiar with working with files in C# and with the basic data structures, as well as string processing in .NET Framework.
Inventing an Idea for a Solution
We get a piece of paper, write few examples and we come up with the following idea: we read the words file, scan through the text and check each word from the text for matches with the preliminary given list of words and increase the counter for each matched word.
Checking the Idea
The above idea for solving the task is trivial but we can still check it by writing down on a piece of paper the sample input (words and text) and the expected result. We just scan through the text word by word in our paper example and when we find a match with some of the preliminary given words (as a substring) we increment the counter for the matched word. The idea works in our example.
Now let’s think of counterexamples. In the same time we might also come with few questions regarding the implementation:
- How do we scan the text and search for matches? We can scan the text character by character or line by line or we can read the entire text in the memory and then scan it in the memory (by string matching or by a regular expression). All of these approaches might work correctly but the performance could vary, right? We will think about the performance a bit later.
- How do we extract the words from the text? Maybe we can read the text and split it by all any non-letter characters? Where shall we take these non-letter characters from? Or we can read the text char by char and once we find a non-letter character we will have the next word from the text? The second idea seems faster and will require less memory because we don’t need to read all the text at once. We should think about this, right?
- How do we match two words? This is a good question. Very good question. Suppose we have a word from the text and we want to match it with the words from the file words.txt. For example, we have “Academy” in the text and we should find whether it matches as substring the “CAD” word from the list of words. This will require searching each word from the list as a substring in each word from the text. Also can we have some word appearing several times inside another? This is possible, right?
From all the above questions we can conclude that we don’t need to read the text word by word. We need to match substrings, not words! The title of the problem is misleading. It says “Counting Words in a Text File” but it should be “Counting Substrings in a Text File”.
It is really good that we found we have to match substrings (instead of words), before we have implemented the code for the above idea, right?
Inventing a Better Idea
Now, considering the requirement for substring matching, we come with few new and probably better ideas about solving the problem:
- Scan the text line by line and for each line from the text and each word check how many times the word appears as substring in the line. The last can be counted with String.IndexOf(…) method in a loop. We already have solved this subproblem in the chapter “Strings and Text Processing” (see the section “Finding All Occurrences of a Substring”).
- Read the entire text and count the occurrences of each word in it (as a substring). This idea is very similar to the previous idea but it will require much memory to read the entire text. Maybe this will not be efficient. We gain nothing, but potentially we will run “out of memory”.
- Scan the text char by char and store the read characters in a buffer. After each character read we check if the text in the buffer ends with some of the words from the list. We will not need to search the words in the buffer because we check for each word after each character is read. We could also clear the buffer when we read any non-letter character (because the list of words for matching should contain letters only). Thus the memory consumption will be very low.
The first and the last idea seem to be good. Which of them to implement? Maybe we could implement both of them and choose the faster one. Having two solutions will also improve the testing because we should get identical results with both of the solutions on all test cases.
Checking the New Ideas
We have two good ideas and we need to check them for correctness before thinking about implementation. How to check the ideas? We can invent a good test case on a piece of paper and try the ideas on it.
Let’s have the following list of words:
|
Word S MissingWord DS aa |
We might be interested to find the number of occurrences of the above words in the following text:
|
Word? We have few words: first word, second word, third word. Some passwords: PASSWORD123, @PaSsWoRd!456, AAaA, !PASSWORD |
The expected result is as follows:
|
Word --> 9 S --> 13 MissingWord --> 0 DS --> 2 aa --> 3 |
In the above example we have many different special cases: whole-word matching, matching as a substring, matching in different casing, matches in the start / end of the text, several matches inside the same word, overlapping matches, etc. This example is a very good representative of the common case for this problem. It is important to have such short but comprehensive test case when solving programming problems. It is important to have it early, when checking the ideas, before any code is written. This avoids mistakes, catches incorrect algorithms and saves time!
Checking the Line by Line Algorithm
Now let’s check the first algorithm: read the two lines of text and check how many times each of the words from the given list occurs in each line ignoring the character casing. At the first line we find as substrings (ignoring the case) “word” 5 times, “s” 3 times, “MissingWord” 0 times, “aa” 0 times and “ds” – 1 time. At the second line we find as substrings (ignoring the case) “word” 4 times, “s” 10 times, “MissingWord” 0 times, “aa” 3 times and “ds” – 1 time. We sum the occurrences and we find that the result is correct.
We try to find counterexamples, but we can’t. The algorithm may not work with words spanning multiple lines. This is not possible by definition. It may also have issues with the overlapping matches like finding “aa” in “AAaA”. This will be definitely checked after the algorithm is implemented.
Checking the Char by Char Algorithm
Let’s check the other algorithm: scan through the text char by char, holding the characters in a buffer. After each character if the buffer ends with some of the words (ignoring the character casing), the occurrences of the matched word are increased. If a non-letter is occurred, the buffer is cleaned.
We start from empty buffer and append the first char from the text “W” to the buffer. None of the words match the end of the buffer. We append “o” and the buffer holds “Wo”. No matches. Then we append “r”. The buffer holds “Wor”. Again no matches are found with any of the words. We append the next char “d” and the buffer holds “Word”. We have found a match with the word form a list: “word”. We increase the number of occurrences of the matched word from zero to one. The next char is “?” and we clean the buffer, because it is not a letter. The next char is “ ” (space). We again clean the buffer. The next char is “W”. We append it to the buffer. No matches with any of the words. We continue further and further… After the last character is processed, the algorithm finishes and the results are correct.
We try to find counterexamples, but we can’t. The algorithm may not work with words spanning multiple lines, but this is not possible by definition.
Decompose the Problem into Subproblems
Now let’s try to divide the problem into subproblems. This should be done separately for the both algorithms we want to try because they differ significantly.
Line by Line Algorithm Decomposed into Subproblems
Let’s decompose the line by line algorithm into subproblems (sub-steps):
1. Read the input words. We can read the file words.txt by using File.ReadAllLines(…). It reads a text file in a string[] array of lines.
2. Process the lines of the text one by one to count the occurrences of each word in it. Initially assign zero occurrences for each word. Read the input file text.txt line by line. For each line from the text and for each word check the number of its occurrences (this is a separate subproblem) and increase the counters for each match. The occurrences counting should be case-insensitive.
3. Count the number of occurrences of certain substring in certain text. This is a separate subproblem. We find the leftmost occurrence of the substring in the text though string.IndexOf(…). If the returned index > -1 (the substring exists), we increase the counter and find the next occurrence of the substring on the right from the last found index. We perform this in a loop until we find -1 as a result which means that there are no more matches. To perform case-insensitive searching we can pass a special parameter StringComparison.OrdinalIgnoreCase to the IndexOf() method.
4. Print the results. Process all words and for each word print it along with its counter holding its occurrences in the output file result.txt.
Char by Char Algorithm Decomposed into Subproblems
Let’s decompose the char by char algorithm into subproblems (sub-steps):
1. Read the input words. We can read the file words.txt by using File.ReadAllLines(…). It reads a text file in a string[] array of lines. The original words can be saved and a copy of them in lowercase can be made to simplify the matching with ignoring the character casing.
2. Process the text char by char. Read the input file text.txt and append the letters into a buffer (StringBuilder). After each letter appended check whether the text in the buffer ends with some of the words in the input list of words (this check is a separate subproblem). If so, increase the number occurrences of the matched word. If a non-letter character is found, clean the buffer. Letters are converted to lowercase before added in the buffer.
3. Check whether a certain text (StringBuilder) ends by a certain string. In case the string has length n lower than the length of the text, the result is false. Otherwise the n letters of the string should be compared one by one with the last n letters of the text. If a mismatch is found, the result is false. If all checks pass, the result is true.
4. Print the results. Process all words and for each word print it along with its counter holding its occurrences in the output file result.txt.
Think about the Data Structures
In the line by line algorithm we don’t have any need of special data structures. We can keep the words in an array or list of strings. We can keep the number of occurrences for each word in array of integer values. The text lines we can keep in strings.
In the char by char algorithm the situation is similar. We don’t need any special data structures. We can keep the words in an array or list of strings. We can keep the number of occurrences for each word in array of integer values. The buffer for the characters we can implement by StringBuilder (because we need to append chars many times).
Think about the Performance
Following the guidelines for problem solving from the chapter “Methodology of Problem Solving” we should think about the efficiency and performance before writing any code.
The line by line algorithm will process the entire text line by line and for each text line it will search for all of the words. Thus if the text has a total size of t characters and the number of words are w, the algorithm will totally perform w string searches in t characters. Each search for a word in the text will pass through the entire text (at least once, but maybe not always). If we assume that searching for a word in a text is a linear time operation, we will have w scans through the entire text, so the excepted running time in quadratic: O(w*t). If we search in MSDN or in Internet, we will be unable to find any information about how exactly String.IndexOf(…) works internally and whether it runs in linear time or it is slower. This method calls a Win32 API function so it cannot be decompiled. Thus the best way to check its performance is by measuring.
The char by char algorithm will process the entire text char by char and for each character it will perform a string matching for each of the words. Suppose the text has t characters and the number of the words is w. In the average case the string matching will run in constant time (it will require just one check if the first letter is not matching, two checks if the first letter matches, etc.). In the worst case the string matching will require n comparisons where n is the length of the word being matched. Thus in the average case the expected running time of the algorithm will be quadratic: O(w*t). In the worst case it will be significantly slower.
It seems like the line by line algorithm is expected to run faster but we are uncertain about how fast is string.IndexOf(…), so this cannot be definitely stated. If we are at an exam, we will probably choose to implement the line by line algorithm. Just for the experiment, let’s implement both of them and compare their performance.
Implementation: Step by Step
If we directly follow the steps, which we have already identified we can write the code with ease. Of course it is better to implement the algorithms step-by-step, to find and fix the bugs early.
Line by Line Algorithm: Step by Step Implementation
We can start implementing the line by line algorithm for word counting in a text file from the method that counts how many times a substring appears in a text. It should look like the following:
|
static int CountOccurrences( string substring, string text) { int count = 0; int index = 0; while (true) { index = text.IndexOf(substring, index); if (index == -1) { // No more matches break; } count++; } return count; } |
Let’s test it before going further:
|
Console.WriteLine( CountOccurrences("hello", "Hello World Hello")); |
The result is 0 – wrong! It seems like we have forgotten to ignore the character casing. Let’s fix this. We need to change the name of the method as well and add the StringComparison.OrdinalIgnoreCase option when searching for the given substring:
|
static int CountOccurrencesIgnoreCase( string substring, string text) { int count = 0; int index = 0; while (true) { index = text.IndexOf(substring, index, StringComparison.OrdinalIgnoreCase); if (index == -1) { // No more matches break; } count++; } return count; } |
Let’s test again with the same example. The program hangs! What happens? We step through the code using the debugger and we find that the variable index takes the first occurrence at position 0 and at the next iteration it takes the same occurrence again at position 0 and the program enters into an endless loop. This is easy to fix. Just start searching from position index+1 (the next position on the right), not from index:
|
static int CountOccurrencesIgnoreCase( string substring, string text) { int count = 0; int index = 0; while (true) { index = text.IndexOf(substring, index + 1, StringComparison.OrdinalIgnoreCase); if (index == -1) { // No more matches break; } count++; } return count; } |
We run the fixed code with the same test. Now the result is incorrect (1 occurrence instead of 2). We again trace the program with the debugger and we find that the first match is at position 12. Immediately we find out why this happens: initially we start from position 1 (index + 1 when index is 0) and we skip the start of the text (position 0).
This is easy to fix:
|
static int CountOccurrencesIgnoreCase( string substring, string text) { int count = 0; int index = -1; while (true) { index = text.IndexOf(substring, index + 1, StringComparison.OrdinalIgnoreCase); if (index == -1) { // No more matches break; } count++; } return count; } |
We test again with the same example and finally the result is correct. We take another, more complex test:
|
Console.WriteLine(CountOccurrencesIgnoreCase( "Word", "Word? We have few words: first word, second word," + "third word. Passwords: PASSWORD123, @PaSsWoRd, !PASSWORD")); |
The result is again correct (9 matches). We test with missing word and the result is again correct (0 matches). This is enough. We assume the method works correctly. Now let’s continue with the next step: read the words.
|
string[] words = File.ReadAllLines("words.txt"); |
There is no need to test this code. It is too simple to have bugs. We will test it when we test the entire solution. Let’s not write the main logic of the program which reads the text line by line and counts the occurrences of each of the input words in each of the lines:
|
int[] occurrences = new int[words.Length]; using (StreamReader text = File.OpenText("text.txt")) { string line; while ((line = text.ReadLine()) != null) { for (int i = 0; i < words.Length; i++) { string word = words[i]; int wordOccurrences = CountOccurrencesIgnoreCase(word, line); occurrences[i] += wordOccurrences; } } } |
This code definitely should be tested but it will be easier to write the code which prints the results to simplify testing. Let’s do this:
|
using (StreamWriter result = File.CreateText("result.txt")) { for (int i = 0; i < words.Length; i++) { result.WriteLine("{0} --> {1}", words[i], occurrences[i]); } } |
The complete implementation of the line by line string occurrences counting algorithms looks as follows:
|
CountSubstringsLineByLine.cs |
|
using System; using System.IO;
public class CountSubstringsLineByLine { static void Main() { // Read the input list of words string[] words = File.ReadAllLines("words.txt");
// Process the file line by line int[] occurrences = new int[words.Length]; using (StreamReader text = File.OpenText("text.txt")) { string line; while ((line = text.ReadLine()) != null) { for (int i = 0; i < words.Length; i++) { string word = words[i]; int wordOccurrences = CountOccurrencesIgnoreCase(word, line); occurrences[i] += wordOccurrences; } } }
// Print the result using (StreamWriter result = File.CreateText("result.txt")) { for (int i = 0; i < words.Length; i++) { result.WriteLine("{0} --> {1}", words[i], occurrences[i]); } } }
static int CountOccurrencesIgnoreCase( string substring, string text) { int count = 0; int index = -1; while (true) { index = text.IndexOf(substring, index + 1, StringComparison.OrdinalIgnoreCase); if (index == -1) { // No more matches break; } count++; } return count; } } |
Testing the Line by Line Algorithm
Now let’s test the entire code of the program. We try our test and it works as expected!
|
text.txt |
|
Word? We have few words: first word, second word, third word. Some passwords: PASSWORD123, @PaSsWoRd!456, AAaA, !PASSWORD |
|
words.txt |
|
Word S MissingWord DS aa |
|
result.txt |
|
Word --> 9 S --> 13 MissingWord --> 0 DS --> 2 aa --> 3 |
We also try the sample test from the problem description and it also works correctly. We try few other tests and all they work correctly. We try also few border cases like empty text and empty list of words. All these cases are handled correctly. It seems like our line by line word counting algorithm and its implementation correctly solve the problem.
We need to conduct only a performance test but let’s first implement the other algorithm to be able to compare which is faster.
Char by Char Algorithm: Step by Step Implementation
Let’s now implement the char by char string occurrences counting algorithm. We will need a StringBuilder to hold the characters we read and a method to check for a match at the end of the StringBuilder. Let’s define this method first. For more flexibility it can be implemented as extension method to the StringBuilder class (recall how extension methods work from the chapter “Lambda Expressions and LINQ”):
|
static bool EndsWith(this StringBuilder buffer, string str) { for (int bufIndex = buffer.Length-str.Length, strIndex = 0; strIndex < str.Length; bufIndex++, strIndex++) { if (buffer[bufIndex] != str[strIndex]) { return false; } } return true; } |
Let’s test the method with a sample text and its ending:
|
Console.WriteLine( new StringBuilder("say hello").EndsWith("hello")); |
This test produces a correct result: True. Let’s test the negative case:
|
Console.WriteLine(new StringBuilder("abc").EndsWith("xx")); |
This test produces a correct result: False. Let’s test what will happen if the ending is longer than the test:
|
Console.WriteLine(new StringBuilder("a").EndsWith("abcdef")); |
We get IndexOutOfRangeException. We found a bug! It is easy to fix – we can return false if the ending string is longer than the text where it should be found:
|
static bool EndsWith(this StringBuilder buffer, string str) { if (buffer.Length < str.Length) { return false; } for (int bufIndex = buffer.Length - str.Length, strIndex = 0; strIndex < str.Length; bufIndex++, strIndex++) { if (buffer[bufIndex] != str[strIndex]) { return false; } } return true; } |
We run all the tests again and all of them pass. We assume the above method is correctly implemented.
Now let’s continue with the step-by-step implementation. Let’s implement the reading of the words:
|
string[] wordsOriginal = File.ReadAllLines("words.txt"); |
This is the same code from the line by line algorithm and it should work.
Let’s now implement the main program logic which reads the text char by char in a buffer of characters and after each letter checks all input words for matches at the ending of the buffer:
|
int[] occurrences = new int[words.Length]; using (StreamReader text = File.OpenText("text.txt")) { StringBuilder buffer = new StringBuilder(); int nextChar; while ((nextChar = text.Read()) != -1) { char ch = (char)nextChar; if (char.IsLetter(ch)) { // A letter is found --> check all words for matches buffer.Append(ch); for (int i = 0; i < words.Length; i++) { string word = words[i]; if (buffer.EndsWith(word)) { occurrences[i]++; } } } else { // A non-letter character is found --> clean the buffer buffer.Clear(); } } } |
To test the code we will need few lines of code to print the output:
|
using (StreamWriter result = File.CreateText("result.txt")) { for (int i = 0; i < words.Length; i++) { result.WriteLine("{0} --> {1}", words[i], occurrences[i]); } } |
Now the program is completed and we should test it.
Testing the Char by Char Algorithm
Let’s test the entire code of the program. We try our test and it fails. The produced result is incorrect:
|
Word --> 1 S --> 6 MissingWord --> 0 DS --> 0 aa --> 0 |
What’s wrong? Maybe the character casing? Do we compare the characters in case-insensitive fashion? No. We found the problem.
How to fix the character casing? Maybe we need to fix the EndsWith(…) method. We search in MSDN and in Internet and we cannot find a method to compare case-insensitively characters. We can do something like this:
|
if (char.ToLower(ch1) != char.ToLower(ch2)) … |
The above code will work but it will convert the characters to lowercase many times, at each character comparison. This may be slow so it is better to lowercase the words and the text preliminary before comparing. If we lowercase the words, they will be printed in lowercase at the output and this will be incorrect. So we need to remember the original words and to make a copy of them in lowercase. Let’s try it. We can use the built-in extension methods from System.Linq to perform the lowercase conversion:
|
string[] wordsOriginal = File.ReadAllLines("words.txt"); string[] wordsLowercase = wordsOriginal.Select(w => w.ToLower()).ToArray(); |
We need to apply few other fixes and finally we get the following full source code of the char by char algorithm for counting the occurrences of a list of substrings in given text:
|
CountSubstringsCharByChar.cs |
|
using System.IO; using System.Linq; using System.Text;
public static class CountSubstringsCharByChar { static void Main() { // Read the input list of words string[] wordsOriginal = File.ReadAllLines("words.txt"); string[] wordsLowercase = wordsOriginal.Select(w => w.ToLower()).ToArray();
// Process the file char by char int[] occurrences = new int[wordsLowercase.Length]; StringBuilder buffer = new StringBuilder(); using (StreamReader text = File.OpenText("text.txt")) { int nextChar; while ((nextChar = text.Read()) != -1) { char ch = (char)nextChar; if (char.IsLetter(ch)) { // A letter is found --> check all words for matches ch = char.ToLower(ch); buffer.Append(ch); for (int i = 0; i < wordsLowercase.Length; i++) { string word = wordsLowercase[i]; if (buffer.EndsWith(word)) { occurrences[i]++; } } } else { // A non-letter is found --> clean the buffer buffer.Clear(); } } }
// Print the result using (StreamWriter result = File.CreateText("result.txt")) { for (int i = 0; i < wordsOriginal.Length; i++) { result.WriteLine("{0} --> {1}", wordsOriginal[i], occurrences[i]); } } }
static bool EndsWith(this StringBuilder buffer, string str) { if (buffer.Length < str.Length) { return false; } for (int bufIndex = buffer.Length-str.Length, strIndex = 0; strIndex < str.Length; bufIndex++, strIndex++) { if (buffer[bufIndex] != str[strIndex]) { return false; } } return true; } } |
We need to test again with our example. Now the program works. The result is correct:
|
Word --> 9 S --> 13 MissingWord --> 0 DS --> 2 aa --> 3 |
We test with all other tests we have (the test from the problem statement, the border cases, etc.) and all of them pass correctly.
Testing for Performance
Now it is time to test for performance both our solutions. We need a big test. We can do it with copy-paste. It is easy to copy-paste the text from our text example 10,000 times and its words 100 times. The repeating words might cause inaccuracies in performance measuring so we manually replace the last 26 words with the letters from “a” to “z”. We also play a bit with the rectangular selection in Visual Studio ([Alt] + mouse selection) and we insert the alphabet as a vertical column in few other places. All this will result in 20,000 lines of text (1.2 MB) and 500 words (3 KB).
To measure the execution time we add two lines of code – before the first line of the Main() method and after the last line of the Main() method:
|
static void Main() { DateTime startTime = DateTime.Now; // The original code goes here Console.WriteLine(DateTime.Now - startTime); } |
Now we execute first the line by line algorithm and it seems not very fast. On average computer from 2008 it prints the following result:
|
00:01:33.6393559 |
After that we execute the char by char algorithm. It produces the following output:
|
00:00:18.1080357 |
Unbelievable! Our char by char processing algorithm is more than 5 times faster than the line by line processing algorithm! But … it still is slow! 18 seconds for 1 MB file is not fast. How about processing 500 MB input and search for 10,000 words?
Invent a Better Idea (Again)
If we are at exam, we could decide whether to take the risk to submit the char by char solution or spend more time to think of faster algorithm. This depends on how much time we have to the end of the exam and how much problems we have already solved, how hard are the unsolved problems, etc. Suppose we have enough time and we want to think more.
What makes our solution slow? If we have 500 words, we check for each of them at each character. We do 500 * length(text) string comparisons. The text is scanned only once (char by char). This cannot be improved, right? If we do not scan the entire text, we will be unable to find all occurrences. So if we want to improve the performance, we should look how to check the words faster after each character is read, right? For 500 words we perform 500 checks after each character is read. This is slow! Can’t we do it faster?
In fact we perform a kind of searching for a matching word in a list of words? From the data structures we know that this takes linear time. Also, from the data structures we know that the fastest data structure for searching is the hash-table. OK, can’t we use a hash table? Instead of searching the words by trying each of them one by one, can’t we directly find the word we need through a hast-table lookup?
We take a sheet of paper and the pencil and we start making sketches and thinking. Suppose we have the text “passwords” and the word “s”. We can check the word that we obtain when we append the letters one after another:
|
p, pa, pas, pass, passw, passwo, passwor, password, passwords |
In this case we will not match the word “s”, right. In fact, when we find a word in the text, we should check all its substrings in the hash table. For example if the text is “password”, all its substrings are:
|
p, pa, a, pas, as, s, pass, ass, ss, s, passw, assw, ssw, sw, w, passwo, asswo, sswo, swo, wo, o, passwor, asswor, sswor, swor, wor, or, r, password, assword, ssword, sword, word, ord, rd, d, passwords, asswords, sswords, swords, words, ords, rds, ds, s |
There are 45 substrings of the word “password”. In a word of n characters we have n*(n+1)/2 substrings. This will work well with short words (e.g. 3-4 characters) and will be slow for the long words (e.g. 15-20 characters).
We get into another idea? This multi-pattern matching problem should have a standard solution. Why don’t we search for it in Internet? We try to search for “multi-pattern matching algorithm” in Google and after exploring the first few results we learn about the “Aho-Corasick string matching algorithm”. Once we know the algorithm name we search for “Aho Corasick C#” and we find a nice C# implementation: https://github.com/tupunco/Tup.AhoCorasick. The theory says that after we have a new idea, we should check it for correctness. The best way to check this idea is by putting the code we found in action. In fact we do not implement the algorithm. We just try to adopt it to solve the problem we have.
Counting Substrings with the Aho-Corasick Algorithm
From the open-source implementation of the Aho-Corasick multi-pattern string matching algorithm mentioned above we can take the class AhoCorasickSearch and put it in action. We write a new solution of the substring counting problem based on what we have learned from the previous solutions. We find all matches of all words by the SearchAll(…) method of the AhoCorasickSearch class. Then we use a hash-table to count the number of occurrences for each of the words. To ensure we ignore the character casing we convert the text and the words into lowercase. This is the code:
|
CountSubstringsAhoCorasick.cs |
|
using System; using System.Collections.Generic; using System.Linq; using System.IO;
class CountSubstringsAhoCorasick { static void Main() { DateTime startTime = DateTime.Now;
// Read the input list of words string[] wordsOriginal = File.ReadAllLines("words.txt"); string[] wordsLowercase = wordsOriginal.Select(w => w.ToLower()).ToArray();
// Read the text string text = File.ReadAllText("text.txt").ToLower();
// Find all word matches and count them var search = new AhoCorasickSearch(); var matches = search.SearchAll(text, wordsLowercase); Dictionary<string, int> occurrences = new Dictionary<string, int>(); foreach (string word in wordsLowercase) { occurrences[word] = 0; } foreach (var match in matches) { string word = match.Match; occurrences[word]++; }
// Print the result using (StreamWriter result = File.CreateText("result.txt")) { foreach (string word in wordsOriginal) { result.WriteLine("{0} --> {1}", word, occurrences[word.ToLower()]); } }
Console.WriteLine(DateTime.Now - startTime); } } |
We test the above code with all tests we already have and it seems to work correctly. We try the performance test and this time we can be amazed by its speed:
|
00:00:00.6540374 |
It runs really fast. This is the solution we needed and if we are allowed to use Internet at the exam, the best way to start when we have a standard well-known problem is to look for a well-known solution.
Students, which are studying in a school, are separated into groups. Each of the groups has a teacher. The following information is kept for the students: first name and last name. The following information is kept for the groups: name, a list of students and teacher. The following information is kept for the teachers: first name, last name and a list of groups he is teaching. Each teacher can teach more than one group. The following information is kept for the school: name, list of the teachers, list of the groups and list of the students. Your task is to:
1. Design a set of classes and relationships between them to model the school, its students, teachers and groups.
2. Implement functionality for add / edit / delete teachers, students, groups and their properties.
3. Implement functionality for printing in human-readable form the school, the teachers, the students, the groups and their properties.
4. Write a sample test program, which demonstrates the work of the implemented classes and methods.
Example of school with teachers, students and groups:
|
School "Freedom". Teachers: Tom Johnson, Elizabeth Hall. Group "English": David Russell, Nicholas Grant, Emma Fletcher, John Brown, Emily Cooper, teacher Elizabeth Hall. Group "French": Kevin Simmons, Ian Hayes, teacher Elizabeth Hall. Group "Informatics": Jessica Carter, Andrew Cooper, Ashley Moore, Olivia Adams, Jonathan Smith, teacher Tom Johnson. |
Start Thinking on the Problem
This is a good example of an exam assignment the purpose of which is to test your abilities to use object-oriented programming (OOP) for modeling problems from the real life, design classes and relationships between them as well as working with collections.
All we need to solve this problem is to use our object-oriented modeling skills that we have gained from chapter “Object-Oriented Programming Principles”, especially from the section “Object-Oriented Modeling (OOM)”.
Inventing an Idea for Solution
In this task there is nothing complex to invent. It is not algorithmic and there is not anything to be thought up. We must define a class for each of the described in the problem description objects (students, teachers, school students, groups, school, etc.) and after that we should define in each class properties to describe its characteristics and methods to implements the actions the class can do, e.g. printing in human-readable form. That’s all.
Following the directions from the section “Object-Oriented Modeling (OOM)” we could identify the nouns in the problem description. Some of them should be modeled as classes; some of them as properties; and some of them may not be important and could be disregarded.
Reading the text from the problem description and analyzing the nouns, we could come to the idea to model the school through defining few interrelated classes: Student, Group, Teacher and School. For testing the classes we could create a class SchoolTest, which will create few objects of each class and will demonstrate their work in action.
Checking the Idea
We will not check the idea because there is nothing to be proven or checked. We need to write few classes to model a real-world situation: a school with students, teachers and groups.
Dividing the Problem into Subproblems
The implementation of each of the classes we already identified can be considered a subproblem of the given school modeling problem. Thus we have the following subproblems:
- Class for the students – Student. Students will have first name, last name and a method for printing in human-readable form – ToString().
- Class for the groups – Group. Groups will have a name, a teacher and a list of students. It will also have а method for printing in human-readable form.
- Class for the teachers – Teacher. Teachers will have first name, last name and a list of groups, as well as а method for printing in human-readable form.
- Class for the school – School. It will have a name and will hold all students, all teachers and all groups.
- Class for testing the other classes – SchoolTest. It will create a school with a few students, a few groups holding subsets of the students and a few teachers. It will assign one teacher per group and a few groups per teacher accordingly. Finally the class will print the school and all its teachers, groups and students.
Think about the Data Structures
The data structures, needed for this problem, are of two main groups: classes and relationships between the classes. Classes will be classes. We have nothing to decide here. The interesting part is how to describe the relationships between the classes, e.g. when a group has a collection of students.
To describe a relationship (link) between two classes we can use an array. With an array we have access to its elements by index, but once it is created we will not be able to add or delete items (arrays have a fixed size). This makes it uncomfortable for our problem, because we don’t know how many students we will have in the school and more students can be added or removed after the school is once created.
List<T> seems more comfortable. It has the advantages of an array and also has a variable length – it is easy to add or delete elements. List<T> can hold lists of students (inside the school and inside a group), lists of teachers (inside a school) and lists of groups (inside a school and inside a teacher).
So far it seems List<T> is the most appropriate for holding aggregations of objects inside another object. To be convinced we will analyze a few more data structures. For example hash-table – it is not appropriate in this case, because the school, teachers, students and groups are not of a key-value type. A hash-table would be appropriate if we need to search a student by its unique student ID, but this is not the case. Structures like stack and queue are inappropriate – we do not have LIFO or FIFO behavior.
The structure “set” and its implementation HashSet<T> may be used when we need to have uniqueness for given key. It would be good sometimes to use this structure to avoid duplicates. We must recall that HashSet<T> requires the methods GetHashCode() and Equals(…) to be correctly defined by the T type. Shall we use sets and where? To answer this question we need to recall the problem description. What is says? We need to design a set of classes to model the school, its students, teachers and groups and functionality for add / edit / delete teachers, students, groups and their properties. The easiest way to implement it is to hold a list of students in the school, a list of groups for each teacher, etc. Lists are easier to implement. Sets give uniqueness, but require Equals() and GetHashCode(). Sets need more effort to be used. So we may use lists to simplify our work.
According to the requirements the school should allow add / edit / delete of students, teachers and groups. The easiest way to implement this is to expose the lists of students, teachers and groups as public properties. List<T> already have methods for add and delete of its elements and its elements are accessible by index and editable. It does the job.
Finally we choose to use List<T> for all aggregations in our classes and we will expose all the class members as properties with read and write access. We do not have a good reason to restrict the access to the members or implement immutable behavior.
Implementation: Step by Step
It’s appropriate to start the implementation with the class Student because it does not depend on any of the other classes.
Step 1: Class Student
In the problem definition we have only two fields representing the first name and the last name of a student. We may add a property Name, which returns a string with the full name of the student and a ToString() implementation to print the student in human-readable form. We might define the class Student as follows:
|
Student.cs |
|
public class Student { public string FirstName { get; set; } public string LastName { get; set; }
public Student(string firstName, string lastName) { this.FirstName = firstName; this.LastName = lastName; }
public string Name { get { return this.FirstName + " " + this.LastName; } }
public override string ToString() { return "Student: " + this.Name; } } |
We want to allow the class members to be editable so we define the FirstName and LastName as public read-write properties.
Testing the Class Student
Before continuing forward we want to test the class Student to be sure it is correct. Let’s create a testing class with a Main() method and create a student in it and print the student:
|
class TestSchool { static void Main() { Student studentPeter = new Student("Peter", "Lee"); Console.WriteLine(studentPeter); } } |
We run the testing program and we get a correct result:
|
Student: Peter Lee |
Now we can continue with the implementation of the other classes.
Step 2: Class Group
The next class we can define is Group. We choose it because the only one required for its definition is the class Student. The properties, which we will define, are the name of the group, a list of the students, which belong to the group, and a teacher who teaches the group. To implement the list with of the students we will use List<Student>. We will add a ToString() method to enable printing the group in a human-readable text form. Let’s see the implementation of the class Group:
|
Group.cs |
|
using System.Collections.Generic;
public class Group { public string Name { get; set; } public List<Student> Students { get; set; }
public Group(string name) { this.Name = name; this.Students = new List<Student>(); }
public override string ToString() { StringBuilder groupAsString = new StringBuilder(); groupAsString.AppendLine("Group name: " + this.Name); groupAsString.Append("Students in the group: " + this.Students); return groupAsString.ToString(); } } |
It is important when we create a group to assign an empty list of students to it. If we leave the list of students unassigned, it will be null and when we try to add a student, we will get an exception.
Testing the Class Group
Let’s now test the Group class. Let’s create a sample group, add few students to it and print the group at the console:
|
static void Main() { Student studentPeter = new Student("Peter", "Lee"); Student studentMaria = new Student("Maria", "Steward"); Group groupEnglish = new Group("English language course"); groupEnglish.Students.Add(studentPeter); groupEnglish.Students.Add(studentMaria); Console.WriteLine(groupEnglish); } |
We run the above testing code and we find a bug:
|
Group name: English language course Students in the group: System.Collections.Generic.List`1[Student] |
It seems like the list of students is printed incorrectly. It is easy to find why. The List<T> class does not correctly implement ToString() and we need to use another way to print a list of students. We can do this with a for-loop but let’s try something shorter and more elegant:
|
using System.Linq; … groupAsString.Append("Students in the group: " + string.Join(", ", this.Students.Select(s => s.Name))); |
The above code uses an extension method and a lambda expression to select all students’ names as IEnumerable<string> and then combines them into a string using a comma as separator. Let’s test the Group class again after the fix:
|
Group name: English language course Students in the group: Peter Lee, Maria Steward |
The group class now works correctly.
Let’s think a bit: who is teaching the students in the group? We should have a teacher, right. Let’s try to add the simplest possible class Teacher and define a property of it in the Group class:
|
public class Teacher { public string FirstName { get; set; } public string LastName { get; set; }
public string Name { get { return this.FirstName + ' ' + this.LastName; } } }
public class Group { public string Name { get; set; } public List<Student> Students { get; set; } public Teacher Teacher { get; set; }
public Group(string name) { this.Name = name; this.Students = new List<Student>(); }
public override string ToString() { StringBuilder groupAsString = new StringBuilder(); groupAsString.AppendLine("Group name: " + this.Name); groupAsString.Append("Students in the group: " + string.Join(", ", this.Students.Select(s => s.Name))); groupAsString.Append("\nGroup teacher: " + this.Teacher.Name); return groupAsString.ToString(); } } |
Let’s test again with our sample groups of two students studying English:
|
Student studentPeter = new Student("Peter", "Lee"); Student studentMaria = new Student("Maria", "Steward"); Group groupEnglish = new Group("English language course"); groupEnglish.Students.Add(studentPeter); groupEnglish.Students.Add(studentMaria); Console.WriteLine(groupEnglish); |
We find another bug:
|
Unhandled Exception: System.NullReferenceException: Object reference not set to an instance of an object. at Group.ToString() … |
We step through the debugger and we see that we try to print the teacher’s name but there is no teacher (it is null). This is easy to fix. We could check whether the teacher exists prior to printing it in the ToString() method:
|
if (this.Teacher != null) { groupAsString.Append("\nGroup teacher: " + this.Teacher.Name); } |
Let’s test again after the fix. Now we get the following correct result:
|
Group name: English language course Students in the group: Peter Lee, Maria Steward |
Let’s now add a teacher to the testing group and check what happens:
|
Student studentPeter = new Student("Peter", "Lee"); Student studentMaria = new Student("Maria", "Steward"); Group groupEnglish = new Group("English language course"); groupEnglish.Students.Add(studentPeter); groupEnglish.Students.Add(studentMaria); Teacher teacherNatasha = new Teacher() { FirstName = "Natasha", LastName = "Walters" }; groupEnglish.Teacher = teacherNatasha; Console.WriteLine(groupEnglish); |
The result is correct:
|
Group name: English language course Students in the group: Peter Lee, Maria Steward Group teacher: Natasha Walters |
Now the Group class works correctly. We can continue with the next class.
Step 3: Class Teacher
Let’s define the class Teacher. We already have some piece of it, but let’s define it in a better way. The teacher should have first name, last name and a list of group he teaches and should be printable in human-readable form. We can define it directly repeating the logic in the Group class:
|
Teacher.cs |
|
public class Teacher { public string FirstName { get; set; } public string LastName { get; set; } public List<Group> Groups { get; set; }
public Teacher(string firstName, string lastName) { this.FirstName = firstName; this.LastName = lastName; this.Groups = new List<Group>(); }
public string Name { get { return this.FirstName + " " + this.LastName; } }
public override string ToString() { StringBuilder teacherAsString = new StringBuilder(); teacherAsString.AppendLine("Teacher name: " + this.Name); teacherAsString.Append("Groups of this teacher: " + string.Join(", ", this.Groups.Select(s => s.Name))); return teacherAsString.ToString(); } } |
Like in the class Group, it is important to create and empty list of groups instead of leaving the Groups property uninitialized.
Testing the Class Teacher
Before going further, let’s test the class Teacher. We can create a teacher with a few groups and print it at the console:
|
static void Main() { Teacher teacherNatasha = new Teacher("Natasha", "Walters"); Group groupEnglish = new Group("English language"); Group groupFrench= new Group("French language"); teacherNatasha.Groups.Add(groupEnglish); teacherNatasha.Groups.Add(groupFrench); Console.WriteLine(teacherNatasha); } |
The result is correct:
|
Teacher name: Natasha Walters Groups of this teacher: English language, French language |
This was expected. We just repeated the same logic like in the Group class which was already tested and all bugs in it was fixed. We found once again how important is to write the code step by step with testing and bug-fixing after each step, right? The bug with incorrectly printing the list of students would have been repeated when printing the list of groups, right?
Step 4: Class School
We finish our object model with the definition of the class School, which uses all of the classes we already defined. It should have a name and should hold a list of students, a list of teachers and a list of groups:
|
public class School { public string Name { get; set; } public List<Teacher> Teachers { get; set; } public List<Group> Groups { get; set; } public List<Student> Students { get; set; }
public School(string name) { this.Name = name; this.Teachers = new List<Teacher>(); this.Groups = new List<Group>(); this.Students = new List<Student>(); } } |
Before testing the class, let’s think what the class School is expected to do. It should hold the students, teachers and groups and should be printable at the console, right? If we print the school, what should be printed? Maybe we should print its name, all its students (with their inner details), all its teachers (with their inner details) and all its groups (with their inner details). Let’s try to define the ToString() method for the class School:
|
public override string ToString() { StringBuilder schoolAsString = new StringBuilder(); schoolAsString.AppendLine("School name: " + this.Name); schoolAsString.AppendLine("Teachers: " + string.Join(", ", this.Teachers.Select(s => s.Name))); schoolAsString.AppendLine("Students: " + string.Join(", ", this.Students.Select(s => s.Name))); schoolAsString.Append("Groups: " + string.Join(", ", this.Groups.Select(s => s.Name))); foreach (var teacher in this.Teachers) { schoolAsString.Append("\n---\n"); schoolAsString.Append(teacher); } foreach (var group in this.Groups) { schoolAsString.Append("\n---\n"); schoolAsString.Append(group); } foreach (var student in this.Students) { schoolAsString.Append("\n---\n"); schoolAsString.Append(student); } return schoolAsString.ToString(); } |
We shall not test the class School, because this will be the main purpose of our last class: SchoolTest.
Step 5: Class SchoolTest
The final thing is the implementation of the class SchoolTest the purpose of which is to demonstrate all the classes we have defined (Student, Group, Teacher and School) and their methods and properties. This is our last subproblem. For the demonstration we create a sample school with a few students, a few teachers and a few groups and we print it:
|
SchoolTest.cs |
|
class TestSchool { static void Main() { // Create a few students Student studentPeter = new Student("Peter", "Lee"); Student studentGeorge = new Student("George", "Redwood"); Student studentMaria = new Student("Maria", "Steward"); Student studentMike = new Student("Michael", "Robinson");
// Create a group and add a few students to it Group groupEnglish = new Group("English language course"); groupEnglish.Students.Add(studentPeter); groupEnglish.Students.Add(studentMike); groupEnglish.Students.Add(studentMaria); groupEnglish.Students.Add(studentGeorge);
// Create a group and add a few students to it Group groupJava = new Group("Java Programming course"); groupJava.Students.Add(studentMaria); groupJava.Students.Add(studentPeter);
// Create a teacher and assign it to few groups Teacher teacherNatasha = new Teacher("Natasha", "Walters"); teacherNatasha.Groups.Add(groupEnglish); teacherNatasha.Groups.Add(groupJava); groupEnglish.Teacher = teacherNatasha; groupJava.Teacher = teacherNatasha;
// Create another teacher and a group he teaches Teacher teacherSteve = new Teacher("Steve", "Porter"); Group groupHTML = new Group("HTML course"); groupHTML.Students.Add(studentMike); groupHTML.Students.Add(studentMaria); groupHTML.Teacher = teacherSteve; teacherSteve.Groups.Add(groupHTML);
// Create a school with few students, groups and teachers School school = new School("Saint George High School"); school.Students.Add(studentPeter); school.Students.Add(studentGeorge); school.Students.Add(studentMaria); school.Students.Add(studentMike); school.Groups.Add(groupEnglish); school.Groups.Add(groupJava); school.Groups.Add(groupHTML); school.Teachers.Add(teacherNatasha); school.Teachers.Add(teacherSteve);
// Modify some of the groups, student and teachers groupEnglish.Name = "Advanced English"; groupEnglish.Students.RemoveAt(0); studentPeter.LastName = "White"; teacherNatasha.LastName = "Hudson";
// Print the school Console.WriteLine(school); } } |
We run the program and we get the expected result:
|
School name: Saint George High School Teachers: Natasha Hudson, Steve Porter Students: Peter White, George Redwood, Maria Steward, Michael Robinson Groups: Advanced English, Java Programming course, HTML course --- Teacher name: Natasha Hudson Groups of this teacher: Advanced English, Java Programming course --- Teacher name: Steve Porter Groups of this teacher: HTML course --- Group name: Advanced English Students in the group: Michael Robinson, Maria Steward, George Redwood Group teacher: Natasha Hudson --- Group name: Java Programming course Students in the group: Maria Steward, Peter White Group teacher: Natasha Hudson --- Group name: HTML course Students in the group: Michael Robinson, Maria Steward Group teacher: Steve Porter --- Student: Peter White --- Student: George Redwood --- Student: Maria Steward --- Student: Michael Robinson |
Of course in real life programs do not start from the first time, but in this task the mistakes you could make are trivial so there’s no point in discussing them. All classes are implemented and tested. We are almost finished with this problem.
Testing the Solution
As usually, it remains to test if the entire solution is working correctly. We’ve already done this. We tested all the classes in their nominal case.
We can do some tests with the border cases, for instance a group without students, empty school, etc. It seems like these cases work correctly. We might test a student without a name, but it is unclear whether the class should keep itself of incorrect names and what is a correct name. We can leave these classes without checks for the names. It will be a responsibility of their caller to put correct names though their constructors and properties. The problem description says nothing about this.
It is interesting how we delete a student. In our current implementation, if we delete a student, we will need to remove it from the school and to remove it from all groups he belongs to. The removal itself will require the student to have the Equals() method defined correctly or we should compare students by hand (property by property). It is unclear from the problem description how exactly the “delete student” operation should work.
We assume we don’t have time and we submit the solution in its current state without efficient delete operation. Sometimes it takes too much time to fix something and it is better to leave it in not perfect form. Below is the full source code of the solution of the school modeling problem:
|
School.cs |
|
using System; using System.Collections.Generic; using System.Linq; using System.Text;
public class Student { public string FirstName { get; set; } public string LastName { get; set; }
public Student(string firstName, string lastName) { this.FirstName = firstName; this.LastName = lastName; }
public string Name { get { return this.FirstName + " " + this.LastName; } }
public override string ToString() { return "Student: " + this.Name; } }
public class Group { public string Name { get; set; } public List<Student> Students { get; set; } public Teacher Teacher { get; set; }
public Group(string name) { this.Name = name; this.Students = new List<Student>(); }
public override string ToString() { StringBuilder groupAsString = new StringBuilder(); groupAsString.AppendLine("Group name: " + this.Name); groupAsString.Append("Students in the group: " + string.Join(", ", this.Students.Select(s => s.Name))); if (this.Teacher != null) { groupAsString.Append("\nGroup teacher: " + this.Teacher.Name); } return groupAsString.ToString(); } }
public class Teacher { public string FirstName { get; set; } public string LastName { get; set; } public List<Group> Groups { get; set; }
public Teacher(string firstName, string lastName) { this.FirstName = firstName; this.LastName = lastName; this.Groups = new List<Group>(); }
public string Name { get { return this.FirstName + " " + this.LastName; } }
public override string ToString() { StringBuilder teacherAsString = new StringBuilder(); teacherAsString.AppendLine("Teacher name: " + this.Name); teacherAsString.Append("Groups of this teacher: " + string.Join(", ", this.Groups.Select(s => s.Name))); return teacherAsString.ToString(); } }
public class School { public string Name { get; set; } public List<Teacher> Teachers { get; set; } public List<Group> Groups { get; set; } public List<Student> Students { get; set; }
public School(string name) { this.Name = name; this.Teachers = new List<Teacher>(); this.Groups = new List<Group>(); this.Students = new List<Student>(); }
public override string ToString() { StringBuilder schoolAsString = new StringBuilder(); schoolAsString.AppendLine("School name: " + this.Name); schoolAsString.AppendLine("Teachers: " + string.Join(", ", this.Teachers.Select(s => s.Name))); schoolAsString.AppendLine("Students: " + string.Join(", ", this.Students.Select(s => s.Name))); schoolAsString.Append("Groups: " + string.Join(", ", this.Groups.Select(s => s.Name))); foreach (var teacher in this.Teachers) { schoolAsString.Append("\n---\n"); schoolAsString.Append(teacher); } foreach (var group in this.Groups) { schoolAsString.Append("\n---\n"); schoolAsString.Append(group); } foreach (var student in this.Students) { schoolAsString.Append("\n---\n"); schoolAsString.Append(student); } return schoolAsString.ToString(); } }
class TestSchool { static void Main() { // Create a few students Student studentPeter = new Student("Peter", "Lee"); Student studentGeorge = new Student("George", "Redwood"); Student studentMaria = new Student("Maria", "Steward"); Student studentMike = new Student("Michael", "Robinson");
// Create a group and add a few students to it Group groupEnglish = new Group("English language course"); groupEnglish.Students.Add(studentPeter); groupEnglish.Students.Add(studentMike); groupEnglish.Students.Add(studentMaria); groupEnglish.Students.Add(studentGeorge);
// Create a group and add a few students to it Group groupJava = new Group("Java Programming course"); groupJava.Students.Add(studentMaria); groupJava.Students.Add(studentPeter);
// Create a teacher and assign it to few groups Teacher teacherNatasha = new Teacher("Natasha", "Walters"); teacherNatasha.Groups.Add(groupEnglish); teacherNatasha.Groups.Add(groupJava); groupEnglish.Teacher = teacherNatasha; groupJava.Teacher = teacherNatasha;
// Create another teacher and a group he teaches Teacher teacherSteve = new Teacher("Steve", "Porter"); Group groupHTML = new Group("HTML course"); groupHTML.Students.Add(studentMike); groupHTML.Students.Add(studentMaria); groupHTML.Teacher = teacherSteve; teacherSteve.Groups.Add(groupHTML);
// Create a school with few students, groups and teachers School school = new School("Saint George High School"); school.Students.Add(studentPeter); school.Students.Add(studentGeorge); school.Students.Add(studentMaria); school.Students.Add(studentMike); school.Groups.Add(groupEnglish); school.Groups.Add(groupJava); school.Groups.Add(groupHTML); school.Teachers.Add(teacherNatasha); school.Teachers.Add(teacherSteve);
// Modify some of the groups, student and teachers groupEnglish.Name = "Advanced English"; groupEnglish.Students.RemoveAt(0); studentPeter.LastName = "White"; teacherNatasha.LastName = "Hudson";
// Print the school Console.WriteLine(school); } } |
We will not run performance tests because the task is not of a computational nature which requires a fast algorithm. Operations that could be slow are deleting of elements from a collection. Creating objects, assigning their properties and adding elements to their collections of child elements are all fast operations. Only the deletion could be slow. We could improve its performance by using HashSet<T> instead of List<T> in all aggregations. We leave this to the reader.
Let’s make just one more note. Why we did not notice the performance problem with deleting elements earlier? Let’s recall how we proceeded with solving this problem. After thinking about the data structures we had to thing about the performance right? Did we do this step? We omitted this step and we found the problem too late. The conclusion is: follow the guidelines for problem solving. They are very wise.
1. Write a program, which prints a square spiral matrix beginning from the number 1 in the upper right corner and moving clockwise. Examples for N=3 and N=4:
2. Write a program, which counts the phrases in a text file. Any sequence of characters could be given as phrase for counting, even sequences containing separators. For instance in the text "I am a student in Sofia" the phrases "s", "stu", "a" and "I am" are found respectively 2, 1, 3 and 1 times.
3. Model with OOP the file system of a computer running Windows. We have devices, directories and files. The devices are for instance floppy disk, HDD, CD-ROM, etc. They have a name and a tree of directories and files. Each directory has a name, date of last change and list of files and directories, which it holds. Each file has a name, date of creation, date of last change and content. Each file is placed in one of the directories. Each file can be text or binary. Text files contain text (string), and the binary ones – sequence of bytes (byte[]). Create a class, which tests the other classes and demonstrates how we can build a model for devices, directories and files in the computer.
4. Using the classes from the previous task write a program which takes the real file system from your computer and loads it in your classes (just the names of the devices, directories and files, without the content of the files because you will run out of memory).
1. The task is analogical to the first task of the sample exam. You can modify the sample solution given above.
2. You may read the text char by char and after each char to append it to the current buffer buf and check each of the searched word for a match with EndsWith() in the buffer’s end. Of course you cannot use efficiently hash-table and you will have a loop for each letter from the text, which is not the fastest solution. This is a modification of the “char by char algorithm for word counting”.
Implementing a faster solution needs to adapt the Aho-Corasick algorithm. Try to play with it and modify the code from the section “Counting Substrings with the Aho-Corasick Algorithm”.
3. The problem is analogical with the “School” problem from the sample exam and it can be solved by using the same approach. Define classes Device, Directory, File, ComputerStorage and ComputerStorageTest. Think of what properties each of these classes has and what are the relationships between the classes. Create a base abstract class File and inherit it from TextFile and BinaryFile. Test your code with sample hierarchy of devices, files and folders. Note: a file can be listed in more than one directory at the same time (unlike in the file system).
4. Use the class System.IO.Directory and its static methods GetFiles(), GetDirectories() and GetLogicalDrives(). Traverse the files system using the BFS or DFS graph traversal algorithm. Load partially the content of long files (e.g. the first 128 bytes / chars) to save memory.
Discussion Forum
Comment the book and the tasks in the : forum of the Software Academy.
Tags: book, C#, C# book, Counting Words in a Text File, English, free, Nakov, programming, read online, review some sample exam problems and suggest solutions, School, Spiral MatrixOne response to “Chapter 26. Sample Programming Exam – Topic #3”
Leave a Reply
You must be logged in to post a comment.

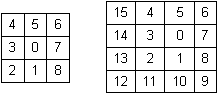
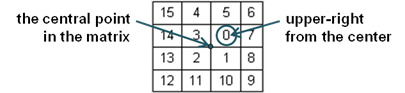
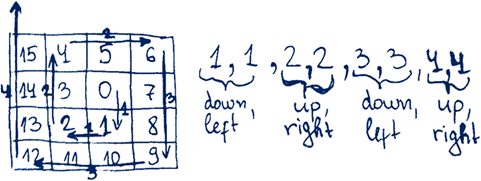

[…] Chapter 26. Sample Programming Exam – Topic #3 […]