Глава 6. Цикли

В тази тема...

В настоящата тема ще разгледаме конструкциите за цикли, с които можем да изпълняваме даден фрагмент програмен код многократно. Ще разгле­даме как се реализират повторения с условие (while и do-while цикли) и как се работи с for-цикли. Ще дадем примери за различните възмож­ности за дефиниране на цикъл, за начина им на конструиране и за някои от основните им приложения. Накрая ще разгледаме, как можем да използ­ваме няколко цикъла, разположени един в друг (вложени цикли).

Съдържание

• Видео
• Презентация
• Мисловни карти
• В тази тема...
• Какво е "цикъл"?
• Конструкция за цикъл while
• Конструкция за цикъл do-while
• Конструкция за цикъл for
• Конструкция за цикъл foreach
• Вложени цикли
• Упражнения
• Решения и упътвания
• Демонстрации (сорс код)
• Дискусионен форум

Видео

Презентация

Мисловни карти

Какво е "цикъл"?

В програмирането често се налага многократно изпълнение на дадена последователност от операции. Цикъл (loop) е основна конструкция в програмирането, която позво­лява многократно изпълнение на даден фраг­мент сорс код. В зависимост от вида на цикъла, програмният код в него се повтаря или фиксиран брой пъти или докато е в сила дадено условие.

Цикъл, който никога не завършва, се нарича безкраен цикъл (infinite loop). Използването на безкраен цикъл рядко се налага, освен в случаи, когато някъде в тялото на цикъла се използва операторът break, за да бъде прекратено неговото изпълнение преждевременно. Ще разгледаме тази възможност по-късно, а сега нека разгледаме конструкциите за цикли в езика C#.

Конструкция за цикъл while

Един от най-простите и най-често използвани цикли е while.

while (условие) {           тяло на цикъла; }

В кода по-горе условие представлява произволен израз, който връща булев резултат – истина (true) или лъжа (fasle). Той определя докога ще се изпълнява тялото на цикъла и се нарича условие на цикъла (loop condition). В примера тяло на цикъла е програмният код, изпълняван при всяко повторение (итерация) на цикъла, т.е. всеки път, когато входното условие е истина. Логически поведението на while циклите може да се опише чрез следната схема:

При while цикъла първоначално се изчислява булевият израз и ако ре­зултатът от него е true, се изпълнява последователността от операции в тялото на цикъла. След това входното условие отново се проверява и ако е истина, отново се изпълнява тялото на цикъла. Всичко това се повтаря отново и отново докато в някакъв момент условният израз върне стойност false. В този момент цикълът приключва своята работа и програмата продължава от следващия ред веднага след тялото на цикъла.

Понеже условието на while цикъла се намира в неговото начало, той често се нарича цикъл с предусловие (pre-test loop). Тялото на while цикъл може и да не се изпълни нито веднъж, ако в самото начало е нарушено условието на цикъла. Ако условието на цикъла никога не бъде нарушено, той ще се изпълнява безкрайно.

Използване на while цикли

Нека разгледаме един съвсем прост пример за използването на while цикъл. Целта на цикъла е да се отпечатват на конзолата числата в интер­вала от 0 до 9 в нарастващ ред:

// Initialize the counter int counter = 0;   // Execute the loop body while the loop condition holds while (counter <= 9) {             // Print the counter value           Console.WriteLine("Number : " + counter);           // Increment the counter           counter++; }

При изпълнение на примерния код получаваме следния резултат:

Number : 0 Number : 1 Number : 2 Number : 3 Number : 4 Number : 5 Number : 6 Number : 7 Number : 8 Number : 9

Нека дадем още примери, за да илюстрираме ползата от циклите и покажем някои задачи, които могат да се решават с помощта на цикли.

Сумиране на числата от 1 до N – пример

В настоящия пример ще разгледаме как с помощта на цикъл while можем да намерим сумата на числата от 1 до n. Числото n се чете от конзолата:

Console.Write("n = "); int n = int.Parse(Console.ReadLine()); int num = 1; int sum = 1; Console.Write("The sum 1"); while (num < n) {             num++;             sum += num;             Console.Write(" + " + num); } Console.WriteLine(" = " + sum);

Първоначално инициализираме променливите num и sum със стойност 1. В num пазим текущото число, което добавяме към сумата на предходните. При всяко преминаване през цикъла увеличаваме num с 1, за да получим следващото число, след което в условието на цикъла проверя­ваме дали то е в интервала от 1 до n. Променливата sum съдържа сумата на числата от 1 до num във всеки един момент. При влизане в цикъла добавяме към нея поредното число записано в num. На конзолата принти­раме всички числа num от 1 до n с разделител "+" и крайния резултат от сумирането след приключване на цикъла. Изходът от програмата е следният (въвеждаме n=17):

n = 17 The sum 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 = 153

Нека дадем още един пример за използване на while, преди да продъл­жим към другите конструкции за организиране на цикъл.

Проверка за просто число – пример

Ще напишем програма, с която да проверяваме дали дадено число е просто. Числото за проверка ще четем от конзолата. Както знаем от математиката, просто е всяко цяло положително число, което освен на себе си и на 1, не се дели на други числа. Можем да проверим дали числото num е просто, като в цикъл проверим дали се дели на всички числа между 2 и √num:

Console.Write("Enter a positive number: "); int num = int.Parse(Console.ReadLine()); int divider = 2; int maxDivider = (int)Math.Sqrt(num); bool prime = true; while (prime && (divider <= maxDivider)) {             if (num % divider == 0)             {                         prime = false;             }             divider++; } Console.WriteLine("Prime? " + prime);

Променливата divider използваме за стойността на евентуалния делител на числото. Първоначално я инициализираме с 2 (най-малкият възможен делител). Променливата maxDivider е максималният възможен делител, който е равен на корен квадратен от числото. Ако имаме делител, по-голям от √num, то би трябвало num да има и друг дели­тел, който е обаче по-малък от √num и затова няма смисъл да проверяваме числата, по-големи от √num. Така намаляваме броя на итерациите на цикъла.

За резултата използваме отделна променлива от булев тип с име  prime. Първоначално, нейната стойност е true. При преминаване през цикъла, ако се окаже, че числото има делител, стойността на prime ще стане false.

Условието на while цикъла се състои от две подусловия, които са свър­зани с логическия оператор && (логическо и). За да бъде изпълнен цикъ­лът, трябва и двете подусловия да са верни едновременно. Ако в някакъв момент намерим делител на числото num, променливата prime става false и условието на цикъла вече не е изпълнено. Това означава, че цикълът се изпълнява до намиране на първия делител на числото или до доказване на факта, че num не се дели на никое от числата в интервала от 2 до √num.

Ето как изглежда резултатът от изпълнението на горния пример при въвеждане съответно на числата 37 и 34 като входни стойности:

Enter a positive number: 37 Prime? True

Enter a positive number: 34 Prime? False

Оператор break

Операторът break се използва за преждевременно излизане от цикъл, преди той да е завършил изпълнението си по естествения си начин. При срещане на оператора break цикълът се прекратява и изпълнението на програмата продължава от следващия ред веднага след тялото на цикъла. Прекра­тяването на цикъл с оператора break може да стане само от неговото тяло, когато то се изпълнява в поредната итерация на цикъла. Когато break се изпълни кодът след него в тялото на цикъла се прескача и не се изпълнява. Ще демонстрираме аварийното излизане от цикъл с break с един пример.

Изчисляване на факториел – пример

В този пример ще пресметнем факториела на въведено от конзолата число с помощта на безкраен while цикъл и оператора break. Да си припомним от математиката какво е факториел и как се изчислява. Факториелът на дадено естествено число n е функция, която изчислява като произведение на всички естествени числа, по-малки или равни на n. Записва се като n! и по дефиниция са в сила формулите:

-    n! = 1*2*3.......(n-1)*n, за  n>1;

-    1! = 1;

-    0! = 1.

Произведението n! може да се изрази чрез факториел от естествени числа, по-малки от n:

-    n! = (n-1)! * n, като използваме началната стойност 0! = 1.

За да изчислим факториела на n ще използваме директно дефиницията:

int n = int.Parse(Console.ReadLine()); // "decimal" is the biggest type that can hold integer values decimal factorial = 1; // Perform an "infinite loop" while (true) {           if (n <= 1)           {                    break;           }           factorial *= n;           n--; } Console.WriteLine("n! = " + factorial);

В началото инициализираме променливата factorial с 1, а n прочитаме от конзолата. Конструираме безкраен while цикъл като използваме true за условие на цикъла. Използваме оператора break, за да прекратим цикъла, когато n достигне стойност по-малка или равна на 1. В противен случай умножаваме текущия резултат по n и намаляваме n с единица. Така на практика първата итерация от цикъла променливата factorial има стойност n, на втората – n*(n-1) и т.н. На последната итерация от цикъла стойността на factorial е произведението n*(n-1)*(n-2)*…*3*2, което е търсената стойност n!.

Ако изпълним примерната програма и въведем 10 като вход, ще получим следния резултат:

10 n! = 3628800

Конструкция за цикъл do-while

Do-while цикълът е аналогичен на while цикъла, само че при него проверката на булевото условие се извършва след изпълнението на операциите в цикъла. Този тип цикли се наричат цикли с условие в края (post-test loop). Един do-while цикъл изглежда по следния начин:

do {           код за изпълнение; } while (израз);

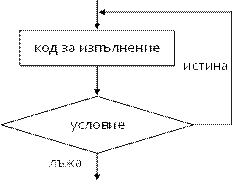
Схематично do-while циклите се изпълняват по следната логическа схема:

Първоначално се изпълнява тялото на цикъла. След това се проверява неговото условие. Ако то е истина, тялото на цикъла се повтаря, а в противен случай цикълът завършва. Тази логика се повтаря докато условието на цикъла бъде нарушено. Тялото на цикъла се повтаря най-малко един път. Ако условието на цикъла постоянно е истина, цикълът никога няма да завърши.

Използване на do-while цикли

Do-while цикълът се използва, когато искаме да си гарантираме, че поредицата от операции в него ще бъде изпълнена многократно и задължително поне веднъж в началото на цикъла.

Изчисляване на факториел – пример

В този пример отново ще изчислим факториела на дадено число n, но този път вместо безкраен while цикъл, ще използваме do-while. Логиката е аналогична на тази в предходния пример:

Console.Write("n = "); int n = int.Parse(Console.ReadLine()); decimal factorial = 1; do {           factorial *= n;           n--; } while (n > 0); Console.WriteLine("n! = " + factorial);

Започваме в началото от резултат 1 и умножаваме последователно на всяка итерация резултата с n и намаляваме n с единица докато n достигне 0. Така получаваме произведението n*(n-1)*…*1. Накрая отпечатваме получения резултат на конзолата. Този алгоритъм винаги извършва поне 1 умножение и затова няма да работи коректно при n=0, но ще работи правилно за n ≥ 1.

Ето го и резултатът от изпълнение на горния пример при n=7:

n = 7 n! = 5040

Факториел на голямо число – пример

Може би се питате какво ще се случи, ако в предходния пример въведем прекалено голяма стойност за числото n, например n=100. Тогава ще при пресмятането на n! ще препълним типа decimal и резултатът ще е изключение System.OverflowException:

n = 100 Unhandled Exception: System.OverflowException: Value was either too large or too small for a Decimal.    at System.Decimal.FCallMultiply(Decimal& result, Decimal d1, Decimal d2)    at System.Decimal.op_Multiply(Decimal d1, Decimal d2)    at TestProject.Program.Main() in C:\Projects\TestProject\Program .cs:line 17

Ако искаме да пресметнем 100!, можем да използваме типа данни BigInteger, който е нов за .NET Framework 4.0 и липсва в по-старите версии. Този тип представлява цяло число, което може да бъде много голямо (примерно 100 000 цифри). Няма ограничение за големината на числата записвани в класа BigInteger (стига да има достатъчно опера­тивна памет).

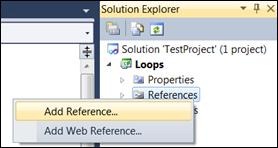
За да използваме BigInteger, първо трябва да добавим референция от нашия проект към асемблито System.Numerics.dll (това е стандартна .NET библиотека за работа с много големи цели числа). Добавянето на референция става с щракване с десния бутон на мишката върху референ­циите на текущия проект в прозореца Solution Explorer на Visual Studio:

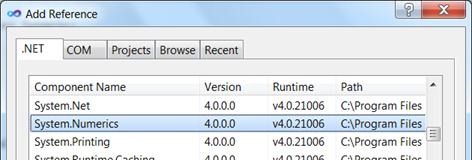
Избираме асемблито System.Numerics.dll от списъка:

Ако търсеното асембли липсва в списъка, то Visual Studio проектът вероятно не таргетира .NET Framework 4.0 и трябва или да създадем нов проект или да сменим версията на текущия:

След това трябва да добавим "using System.Numerics;" преди началото на класа на нашата програма и да сменим decimal с BigInteger. Програмата добива следния вид:

using System; using System.Numerics;   class Factorial {           static void Main()           {                    Console.Write("n = ");                    int n = int.Parse(Console.ReadLine());                    BigInteger factorial = 1;                    do                    {                              factorial *= n;                              n--;                    } while (n > 0);                    Console.WriteLine("n! = " + factorial);           } }

Ако сега изпълним програмата за n=100, ще получим стойността на 100 факториел, което е 158-цифрено число:

n = 100 n! = 933262154439441526816992388562667004907159682643816214685929 63895217599993229915608941463976156518286253697920827223758251185 210916864000000000000000000000000

Произведение в интервала [N...M] – пример

Нека дадем още един, по-интересен, пример за работа с do-while цикли. Задачата е да намерим произведението на всички числа в интервала [n…m]. Ето едно примерно решение на тази задача:

Console.Write("n = "); int n = int.Parse(Console.ReadLine()); Console.Write("m = "); int m = int.Parse(Console.ReadLine()); int num = n; long product = 1; do {           product *= num;           num++; } while (num <= m); Console.WriteLine("product[n..m] = " + product);

В примерния код на променливата num присвояваме последователно на всяка итерация на цикъла стойностите n, n+1, …, m и в променливата product натрупваме произведението на тези стойности. Изискваме от потребителя да въведе n, което да е по-малко от m. В противен случай ще получим като резултат числото n.

Ако стартираме програмата за n=2 и m=6, ще получим следния резултат:

n = 2 m = 6 product[n..m] = 720

Конструкция за цикъл for

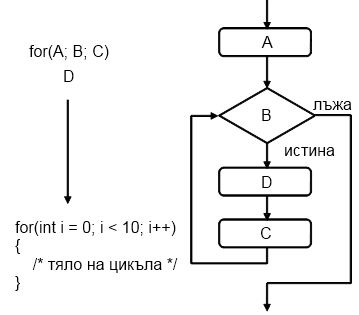
For-циклите са малко по-сложни от while и do-while циклите, но за сметка на това могат да решават по-сложни задачи с по-малко код. Ето как изглежда логическата схема, по която се изпълняват for-циклите:

Те съдържат инициализационен блок (A), условие на цикъла (B), тяло на цикъла (D) и команди за обновяване на водещите променливи (C). Ще ги обясним в детайли след малко. Преди това нека разгледаме как изглежда програм­ният код на един for-цикъл:

for (инициализация; условие; обновяване) {           тяло на цикъла; }

Той се състои от инициализационна част за брояча (в схемата int i = 0), булево условие (i < 10), израз за обновяване на брояча (i++, може да бъде i-- или например i = i + 3) и тяло на цикъла.

Броячът на for цикъла го отличава от останалите видове цикли. Най-често броячът се променя от дадена начална стойност към дадена крайна стойност в нарастващ ред, примерно от 1 до 100. Броят на итерациите на даден for-цикъл най-често е известен още преди да започне изпълне­нието му. Един for-цикъл може да има една или няколко водещи променливи, които се движат в нарастващ ред или в намаляващ ред или с някаква стъпка. Възможно е едната водеща променлива да расте, а другата – да намалява. Възможно е дори да направим цикъл от 2 до 1024 със стъпка умножение по 2, тъй като обновяването на водещите променливи може да съдържа не само събиране, а всякакви други аритметични операции.

Тъй като никой от изброените елементи на for-циклите не е задължи­телен, можем да ги пропуснем всичките и ще получим безкраен цикъл:

for ( ; ; ) {           тяло на цикъла; }

Нека сега разгледаме в детайли отделните части на един for-цикъл.

Инициализация на for цикъла

For-циклите могат да имат инициализационен блок:

for (int num = 0; ...; ...) {           // Променливата num е видима тук и може да се използва } // Тук num не може да се използва

Той се изпълнява само веднъж, точно преди влизане в цикъла. Обикно­вено инициализационният блок се използва за деклариране на промен­ливата-брояч (нарича се още водеща променлива) и задаване на нейна начална стойност. Тази променлива е "видима" и може да се използва само в рамките на цикъла. Възможно е инициализационният блок да декларира и инициализира повече от една променлива.

Условие на for цикъла

For-циклите могат да имат условие за повторение:

for (int num = 0; num < 10; ...) {           тяло на цикъла; }

Условието за повторение (loop condition) се изпълнява веднъж, преди всяка итерация на цикъла, точно както при while циклите. При резултат true се изпълнява тялото на цикъла, а при false то се пропуска и цикълът завършва (преминава се към остана­лата част от програмата, веднага след цикъла).

Обновяване на водещата променлива

Последната част от един for-цикъл съдържа код, който обновява воде­щата променлива:

for (int num = 0; num < 10; num++) {           тяло на цикъла; }

Този код се изпълнява след всяка итерация, след като е приключило изпълнението на тялото на цикъла. Най-често се използва за обновяване стойността на брояча.

Тяло на цикъла

Тялото на цикъла съдържа произволен блок със сорс код. В него са достъпни водещите променливи, декларирани в инициализационния блок на цикъла.

For-цикъл – примери

Ето един цялостен пример за for-цикъл:

for (int i = 0; i <= 10; i++) {           Console.Write(i + " "); }

Резултатът от изпълнението му е следният:

0 1 2 3 4 5 6 7 8 9 10

Ето още един по-сложен пример за for-цикъл, в който имаме две водещи променливи i и sum, които първоначално имат стойност 1, но ги обновя­ваме последователно след всяка итерация на цикъла:

for (int i = 1, sum = 1; i <= 128; i = i * 2, sum += i) {           Console.WriteLine("i={0}, sum={1}", i, sum); }

Резултатът от изпълнението на цикъла е следният:

i=1, sum=1 i=2, sum=3 i=4, sum=7 i=8, sum=15 i=16, sum=31 i=32, sum=63 i=64, sum=127 i=128, sum=255

Изчисляване на N^M – пример

Като следващ пример ще напишем програма, която повдига числото n на степен m, като за целта ще използваме for-цикъл:

Console.Write("n = "); int n = int.Parse(Console.ReadLine()); Console.Write("m = "); int m = int.Parse(Console.ReadLine()); decimal result = 1; for (int i = 0; i < m; i++) {           result *= n; } Console.WriteLine("n^m = " + result);

Първоначално инициализи­раме резултата (result = 1). Цикълът започ­ваме със задаване на начална стойност за променливата-брояч (int i = 0). Определяме условието за изпълнение на цикъла (i < m). Така цикълът ще се изпълнява от 0 до m-1 или точно m пъти. При всяко изпълнение на цикъла умножаваме резултата по n и така n ще се вдига на поредната степен (1, 2, … m) на всяка итерация. Накрая отпечатаме резултата, за да видим правилно ли работи програмата.

Ето как изглежда изходът от програмата при n=2 и m=10:

n = 2 m = 10 n^m = 1024

For-цикъл с няколко променливи

Както вече видяхме, с конструкцията за for-цикъл можем да ползваме едновременно няколко променливи. Ето един пример, в който имаме два брояча. Единият брояч се движи от 1 нагоре, а другият се движи от 10 надолу:

for (int small=1, large=10; small<large; small++, large--) {           Console.WriteLine(small + " " + large); }

Условието за прекратяване на цикъла е застъпване на броячите. В крайна сметка се получава следният резултат:

1 10 2 9 3 8 4 7 5 6

Оператор continue

Операторът continue спира текущата итерация на най-вътрешния цикъл, без да излиза от него. С помощта на следващия пример ще разгледаме как точно се използва този оператор.

Ще намерим сумата на всички нечетни естествени числа в интервала [1...n], който не се делят на 7 чрез for-цикъл:

int n = int.Parse(Console.ReadLine()); int sum = 0; for (int i = 1; i <= n; i += 2) {           if (i % 7 == 0)           {                    continue;           }           sum += i; } Console.WriteLine("sum = " + sum);

Първоначално инициализираме водещата променлива на цикъла със стойност 1, тъй като това е първото нечетно естествено число в интервала [1...n]. След всяка итерация на цикъла проверяваме дали i е все още не е надвишило n (i <= n). В израза за обновяване на променливата я увели­ча­ваме с 2, за да преминаваме само през нечетните числа. В тялото на цикъла правим проверка дали текущото число се дели на 7. Ако това е изпълнено извикваме оператора continue, който прескача останалата част от тялото на цикъла (пропуска добавянето текущото число към сумата). Ако числото не се дели на седем, се преминава към обновяване на сумата с текущото число. Резултатът от примера при n=11 е следният:

11 sum = 29

Конструкция за цикъл foreach

Цикълът foreach (разширен for-цикъл) е нов за C/C++/C# фамилията от езици, но е добре познат на VB и PHP програмистите. Тази конструкция служи за обхождане на всички елементи на даден масив, списък или друга колекция от елементи. Подробно с масивите ще се запознаем в темата "Масиви", но за момента можем да си представяме един масив като наредена последователност от числа или други елементи.

Ето как изглежда един foreach цикъл:

foreach (variable in collection) {           statements; }

Както виждате, той е значително по-прост от стандартния for-цикъл и затова много-често се предпочита от програмистите, тъй като спестява писане, когато трябва да се обходят всички елементи на дадена колекция. Ето един пример, който показва как можем да използваме foreach:

int[] numbers = { 2, 3, 5, 7, 11, 13, 17, 19 }; foreach (int i in numbers) {           Console.Write(" " + i); } Console.WriteLine(); String[] towns = { "Sofia", "Plovdiv", "Varna", "Bourgas" }; foreach (String town in towns) {           Console.Write(" " + town); }

В примера се създава масив от числа и след това те се обхождат с foreach цикъл и се отпечатват на конзолата. След това се създава масив от имена на градове (символни низове) и по същия начин те обхождат и отпечатват на конзолата. Резултатът от примера е следният:

2 3 5 7 11 13 17 19 Sofia Plovdiv Varna Bourgas

Вложени цикли

Вложените цикли представляват конструкция от няколко цикъла, разпо­ложени един в друг. Най-вътрешния цикъл се изпълнява най-много пъти, а най-външният – най-малко. Да разгледаме как изглеждат два вложени цикъла:

for (инициализация; проверка; обновяване) {           for (инициализация; проверка; обновяване)           {                    код за изпълнение;           }           … }

След инициализация на първия for цикъл ще започне да се изпълнява неговото тяло, което съдържа втория (вложения) цикъл. Ще се инициали­зира променливата му, ще се провери условието му и ще се изпълни кода в тялото му, след което ще се обнови промен­ливата му и изпълнението му ще продължи, докато условието му не върне false. След това ще продължи втората итерация на първия for цикъл, ще се извърши обновяване на неговата променлива и отново ще бъде изпълнен целия втори цикъл. Вътрешният цикъл ще се изпълни толкова пъти, колкото се изпълнява тялото на външния цикъл.

Нека сега разгледаме един реален пример, с който ще демонстрираме колко полезни са вложените цикли.

Отпечатване на триъгълник – пример

Нека си поставим следната задача: по дадено число n да отпечатаме на конзолата триъгълник с n на брой реда, изглеждащ по следния начин:

1 1 2 1 2 3 . . . 1 2 3 . . . n

Ще решим задачата с два for-цикъла. Външният цикъл ще обхожда редовете, а вътрешният – елементите в тях. Когато сме на първия ред, трябва да отпечатаме "1" (1 елемент, 1 итерация на вътрешния цикъл). На втория ред трябва да отпечатаме "1 2" (2 елемента, 2 итерации на вътрешния цикъл). Виждаме, че има зависимост между реда, на който сме и броя на елементите, който ще отпечатваме. Това ни подсказва как да организираме конструкцията на вътрешния цикъл:

-    инициализираме водещата му променлива с 1 (първото число, което ще отпечатаме): col = 1;

-    условието за повторение зависи от реда, на който сме: col <= row;

-    на всяка итерация на вътрешния цикъл увеличаваме с единица водещата променлива.

На практика трябва да направим един for-цикъл (външен) от 1 до n (за редовете) и в него още един for-цикъл (вътрешен) за числата в текущия ред, който да върти от 1 до номера на текущия ред. Външният цикъл трябва да ходи по редовете, а вътрешният – по колоните от текущия ред. В крайна сметка получаваме следния код:

int n = int.Parse(Console.ReadLine()); for (int row = 1; row <= n; row++) {           for (int col = 1; col <= row; col++)           {                    Console.Write(col + " ");           }           Console.WriteLine(); }

Ако го изпълним, ще се убедим, че работи коректно. Ето как изглежда резултатът при n=7:

1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7

Прости числа в даден интервал – пример

Нека разгледаме още един пример за вложени цикли. Поставяме си за цел да отпечатаме на конзолата всички прости числа в интервала [n, m]. Интервалът ще ограничим с for-цикъл, а за проверката за просто число ще използваме вложен while цикъл:

Console.Write("n = "); int n = int.Parse(Console.ReadLine()); Console.Write ("m = "); int m = int.Parse(Console.ReadLine ()); for (int num = n; num <= m; num++) {           bool prime = true;           int divider = 2;           int maxDivider = (int) Math.Sqrt(num);           while (divider <= maxDivider)           {                    if (num % divider == 0)                    {                              prime = false;                              break;                    }                    divider++;           }           if (prime)           {                    Console.Write (" " + num);           } }

С външния for-цикъл проверяваме всяко от числата n, n+1, …, m дали е просто. При всяка итерация на външния for-цикъл правим проверка дали водещата му променлива num е просто число. Логиката, по която правим провер­ката за просто число, вече ни е позната. Първоначално инициали­зираме променливата prime с true. С вътрешния while цикъл проверя­ваме всяко от числата [2…√num] дали е делител на num и ако е така, установяваме prime във false. След завършване на while цикъла булевата променлива prime показва дали числото е просто или не. Ако поредното число е просто, го отпечатваме на конзолата.

Ако изпълним примера за n=3 и m=75 ще получим следния резултат:

n = 3 m = 75 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73

Щастливи числа – пример

Нека разгледаме още един пример, с който ще покажем, че можем да влагаме и повече от два цикъла един в друг. Целта е да намерим и отпечатаме всички четирицифрени числа от вида ABCD, за които: A+B = C+D (наричаме ги щастливи числа). Това ще реализираме с помощта на четири for-цикъла – за всяка цифра по един. Най-външният цикъл ще ни определя хилядите. Той ще започва от 1, а останалите от 0. Останалите цикли ще ни определят съответно стотиците, десетиците и единиците. Ще правим проверка дали текущото ни число е щастливо в най-вътрешния цикъл и ако е така, ще го отпечатваме на конзолата. Ето примерна реализация:

for (int a = 1; a <= 9; a++) {           for (int b = 0; b <= 9; b++)           {                    for (int c = 0; c <= 9; c++)                    {                              for (int d = 0; d <= 9; d++)                              {                                       if ((a + b) == (c + d))                                       {                                                 Console.WriteLine(                                                           " " + a + " " + b + " " + c + " " + d);                                       }                              }                    }           } }

Ето част от отпечатания резултат (целият е много дълъг):

1 0 0 1 1 0 1 0 1 1 0 2 1 1 1 1 1 1 2 0 1 2 0 3 1 2 1 2 1 2 2 1 …

Оставяме за домашно на старателния читател да предложи по-ефективно решение на същата задача, което ползва само три вложени цикъла, а не четири.

ТОТО 6/49 – пример

В следващия пример ще намерим всички възможни комбинации от тотото в играта "6/49". Трябва да намерим и отпечатаме всички възможни извадки от 6 различни числа, всяко от които е в интервала [1...49]. Ще използваме 6 for-цикъла. За разлика от предния пример, числата не могат да се повтарят. За да избегнем повторенията ще се стремим всяко следващо число да е по-голямо от предходното. Затова вътрешните цикли няма да започват от 1, а от числото, до което е стигнал предходния цикъл + 1. Първият цикъл ще трябва да го въртим до 44 (а не до 49), вторият до 45, и т.н. Последният цикъл ще е до 49. Ако въртим всички цикли до 49, ще получим съвпадащи числа в някои от комбинациите. По същата причина всеки следващ цикъл започва от брояча на предходния + 1. Нека да видим какво ще се получи:

Всичко изглежда правилно. Да стартираме програмата. Изглежда, че работи, но има един проблем – комбинациите са прекален много и програмата не завършва (едва ли някой ще я изчака). Това е в реда на нещата и е една от причините да има ТОТО 6/49 – комбинациите наистина са много. Оставяме за упражнение на любознателния читател да промени горния пример така че само да пребори колко са всичките комбинации от тотото, вместо да ги отпечата. Тази промяна ще намали драстично обемът на отпечатаните на конзолата резултати и програмата ще завърши удивително бързо.

Упражнения

1.      Напишете програма, която отпечатва на конзолата числата от 1 до N. Числото N трябва да се чете от стандартния вход.

2.      Напишете програма, която отпечатва на конзолата числата от 1 до N, които не се делят едновременно на 3 и 7. Числото N да се чете от стандартния вход.

3.      Напишете програма, която чете от конзолата поредица от цели числа и отпечатва най-малкото и най-голямото от тях.

4.      Напишете програма, която отпечатва всички възможни карти от стан­дартно тесте карти без джокери (имаме 52 карти: 4 бои по 13 карти).

5.      Напишете програма, която чете от конзолата числото N и отпечатва сумата на първите N члена от редицата на Фибоначи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...

6.      Напишете програма, която пресмята N!/K! за дадени N и K (1<K<N).

7.      Напишете програма, която пресмята N!*K!/(N-K)! за дадени N и K (1<K<N).

8.      В комбинаториката числата на Каталан (Catalan’s numbers) се изчис­ляват по следната формула: , за n ≥ 0. Напи­шете програма, която изчислява n-тото число на Каталан за дадено n.

9.      Напишете програма, която за дадено цяло число n, пресмята сумата:

10.   Напишете програма, която чете от конзолата положително цяло число N (N < 20) и отпечатва матрица с числа като на фигурата по-долу:

                                                                              N = 3                                         N = 4

1 2 3 2 3 4 3 4 5

1 2 3 4 2 3 4 5 3 4 5 6 4 5 6 7

11.   Напишете програма, която пресмята с колко нули завършва факториелът на дадено число. Примери:

                   N = 10 -> N! = 3628800 -> 2

                   N = 20 -> N! = 2432902008176640000 -> 4

12.   Напишете програма, която преобразува дадено число от десетична в двоична бройна система.

13.   Напишете програма, която преобразува дадено число от двоична в десетична бройна система.

14.   Напишете програма, която преобразува дадено число от десетична в шестнайсетична бройна система.

15.   Напишете програма, която преобразува дадено число от шестнайсе­тична в десетична бройна система.

16.   Напишете програма, която по дадено число N отпечатва числата от 1 до N, разбъркани в случаен ред.

17.   Напишете програма, която за дадени две числа, намира най-големия им общ делител.

18.   Напишете програма, която по дадено число n, извежда матрица във формата на спирала:

1	2	3	4
12	13	14	5
11	16	15	6
10	9	8	7

 

   пример при n=4

 

 

Решения и упътвания

1.      Използвайте for цикъл.

2.      Използвайте for цикъл и оператора % за намиране на остатък при целочислено деление. Едно число num не се дели на 3 и на 7 едновременно, ако (num % (3*7) == 0).

3.      Първо прочетете броя числа, примерно в променлива n. След това въведете n числа последователно с един for цикъл. Докато въвеждате всяко следващо число запазвайте в две променливи най-малкото и най-голямото число до момента.

4.      Номерирайте картите от 2 до 14 (тези числа ще съответстват на картите от 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A). Номерирайте боите от 1 до 4 (1 – спатия, 2 – каро, 3 – купа, 4 – пика). Сега вече можете да завъртите 2 вложени цикъла и да отпечатате всяка от картите.

5.      Числата на Фибоначи започват от 0 и 1, като всяко следващо се получава като сума от предходните две. Можете да намерите първите n числа на Фибоначи с for цикъл от 1 до n, като на всяка итерация пресмятате поредното число, използвайки предходните две (които ще пазите в две допълнителни променливи).

6.      Умножете числата от K+1 до N.

7.      Вариант за решение е поотделно да пресмятате всеки от факто­риелите и накрая да извършвате съответните операции с резултатите. Помис­лете как можете да оптимизирате пресмятанията, за да не смятате прекалено много факториели! При обикновени дроби, съставени от факто­риели има много възможности за съкращение на еднакви множи­тели в числителя и знаменателя. Тези оптимизации не само ще нама­лят изчисленията и ще увеличат производителността, но ще ви избавят и от препълвания в някои ситуации.

8.      Погледнете предходната задача.

9.      Задачата може да решите с for-цикъл за k=0…n, като ползвате три допълнителни променливи factoriel, power и sum, в които да пазите за k-тата итерация на цикъла съответно k!, x^k и сумата на първите k члена на редицата. Ако реализацията ви е добра, Трябва да имате само един цикъл и не трябва да ползвате външни функции за изчис­ление на факториел и за степенуване.

10.   Трябва да използвате два вложени цикъла, по подобие на задачата за отпечатване на триъгълник с числа. Външният цикъл трябва да върти от 1 до N, а вътрешният – от стойността на външния до стойността на външния + N - 1.

11.   Броят на нулите в края на n! зависи от това, колко пъти числото 10 е делител на факториела. Понеже произведението 1*2*3…*n има повече на брой делители 2, отколкото 5, а 10 = 2 * 5, то броят нули в n! е точно толкова, колкото са множителите със стойност 5 в произведе­нието 1*2*3….*n. Понеже всяко пето число се дели на 5, а всяко 25-то число се дели на 5 двукратно и т.н., то броя нули в n! е сумата: n/5 + n/25 + n/125 + …

12.   Прочетете в Уикипедия какво представляват бройните системи: http://en.wikipedia.org/wiki/Numeral_system. След това помислете как можете да преминавате от десетична в друга бройна система. Помис­лете и за обратното – преминаване от друга бройна система към десе­тична. Ако се затрудните, вижте главата "Бройни системи".

13.   Погледнете предходната задача.

14.   Погледнете предходната задача.

15.   Погледнете предходната задача.

16.   Потърсете в Интернет информация за класа System.Random. Прочетете в Интернет за масиви (или в следващата глава). Направете масив с N елемента и запишете в него числата от 1 до N. След това достатъчно много пъти (помислете точно колко) разменяйте двойки случайни числа от масива.

17.   Потърсете в интернет за алгоритъма на Евклид.

18.   Трябва да използвате двумерен масив. Потърсете в интернет или вижте главата "Масиви"

Демонстрации (сорс код)

Изтеглете демонстрационните примери към настоящата глава от книгата: Цикли-Демонстрации.zip.

Дискусионен форум

Коментирайте книгата и задачите в нея във: форума на софтуерната академия.