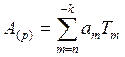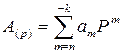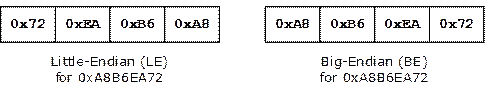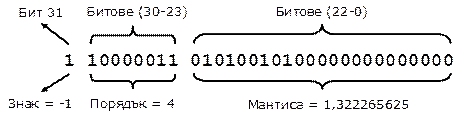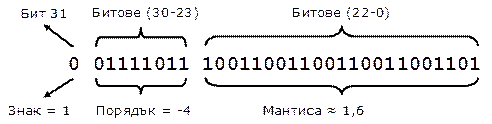Глава 8. Бройни системи

В тази тема...

В настоящата тема ще разгледаме работата с различни бройни системи и представянето на числата в тях. Повече внимание ще отделим на предста­вянето на числата в десетична, двоична и шестнаде­сетична бройна система, тъй като те се използват масово в компютърната техника и в програмирането. Ще обясним и начините за кодиране на числовите данни в компютъра – цели числа без и със знак и различни видове реални числа.

Съдържание

• Видео
• Презентация
• Мисловни карти
• В тази тема...
• История в няколко реда
• Бройни системи
• Представяне на числата
• Упражнения
• Решения и упътвания
• Дискусионен форум

Видео

Презентация

Мисловни карти

История в няколко реда

Използването на различни бройни системи е започнало още в дълбока древност. Това твърдение се доказва от обстоятелството, че още в Египет са използвани слънчевите часовници, а техните принципи за измерване на времето ползват бройни системи. По-голямата част от историците смятат древноегипетската цивилизация за първата цивилизация, която е разделила деня на по-малки части. Те постигат това, посредством употре­бата на първите в света слънчеви часовници, които не са нищо друго освен обикновени пръти, забити в земята и ориентирани по дължината и посоката на сянката.

По-късно е изобретен по-съвършен слънчев часовник, който прилича на буквата Т и е градуиран по начин, по който да разделя времето между изгрев и залез слънце на 12 части. Това доказва използването на дванадесетична бройна система в Египет, важността на числото 12 обикновено се свързва и с обстоятелството, че лунните цикли за една година са 12, или с броя на фалангите на пръстите на едната ръка (по три на всеки от четирите пръста, като не се смята палеца).

В днешно време десетичната бройна система е най-разпространената бройна система. Може би това се дължи на улесненията, които тя предо­ставя на човека, когато той брои с помощта на своите пръсти.

Древните цивилизации са разделили денонощието на по-малки части, като за целта са използвали различни бройни системи, дванадесетични и шестдесетични съответно с основи – 12 и 60. Гръцки астрономи като Хипарх са използвали астрономични подходи, които преди това са били използвани и от вавилонците в Месопотамия. Вавилонците извършвали астрономич­ните изчисления в шестдесетична система, която били насле­дили от шумерите, а те от своя страна са я развили около 2000 г. пр. н. е. Не е известно от какви съображения е избрано точно числото 60 за основа на бройната система, но е важно да се знае че, тази система е много подходяща за представяне на дроби, тъй като числото 60 е най-малкото число, което се дели без остатък съответно на 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 и 30.

Някои приложения на шестдесетичната бройна система

Днес шестдесетичната система все още се използва за измерване на ъгли, географски координати и време. Те все още намират приложение при часовниковия циферблат и сферата на глобуса. Шестдесетичната бройна система е използвана и от Ератостен за разделянето на окръжността на 60 части с цел създаване на една ранна система от географски ширини, съставена от хоризонтални линии, минаващи през известни в миналото места от земята. Един век след Ератостен Хипарх нормирал тези линии, като за целта ги направил успоредни и съобразени с геометрията на Земята. Той въвежда система от линии на географската дължина, в които включват 360 градуса и съответно минават от север до юг и от полюс до полюс. В книгата "Алмагест" (150 г. от н. е.) Клавдий Птолемей доразвива разработките на Хипарх чрез допълнително разделяне на 360-те градуса на географската ширина и дължина на други по-малки части. Той разделил всеки един от градусите на 60 равни части, като всяка една от тези части в последствие била разделена на нови 60 по-малки части, които също били равни. Така получените при деленето части, били наречени partes minutae primae, или "първа минута" и съответно partes minutae secundae, или "втора минута". Тези части се ползват и днес и се наричат съответно "минути" и "секунди".

Кратко обобщение

Направихме кратка историческа разходка през хилядолетията, от която научаваме, че бройните системи са били създадени, използвани и развивани още по времето на шумерите. От изложените факти става ясно защо денонощието съдържа (само) 24 часа, часът съдържа 60 минути, а минутата 60 секунди. Това се дължи на факта, че древните египтяни са разделили по такъв начин денонощието, като са въвели употребата на дванадесетична бройна система. Разделянето на часовете и минутите на 60 равни части, е следствие от работата на древногръцките астрономи, които извършват изчисленията в шестдесетична бройна система, която е създадена от шумерите и използвана от вавилонците.

Бройни системи

До момента разгледахме историята на бройните системи. Нека сега разгледаме какво представляват те и каква е тяхната роля в изчислител­ната техника.

Какво представляват бройните системи?

Бройните системи (numeral systems) са начин за представяне (запис­ване) на числата, чрез краен набор от графични знаци наречени цифри. Към тях трябва да се добавят и правила за представяне на числата. Символите, които се използват при представянето на числата в дадена бройна система, могат да се възприемат като нейна азбука.

По време на различните етапи от развитието на човечеството, различни бройни системи са придобивали известност. Трябва да се отбележи, че днес най-широко разпространение е получила арабската бройна система. Тя използва цифрите 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, като своя азбука. (Интересен е фактът, че изписването на арабските цифри в днешно време се различава от представените по-горе десет цифри, но въпреки това, те пак се отнасят за същата бройна система, т.е. десетичната).

Освен азбука, всяка бройна система има и основа. Основата е число, равно на броя различни цифри, използвани от системата за записване на числата в нея. Например арабската бройна система е десетична, защото има 10 цифри. За основа може да се избере произволно число, чиято абсолютна стойност трябва да бъде различна от 0 и 1. Тя може да бъде и реално или комплексно число със знак.

В практическо отношение, възниква въпросът: коя е най-добрата бройна система, която трябва да използваме? За да си отговорим на този въпрос, трябва да решим, как ще се представи по оптимален начин едно число като записване (т.е. брой на цифрите в числото) и брой на цифрите, които използва съответната бройна система, т.е. нейната основа. По математи­чески път, може да се докаже, че най-доброто съотношение между дължи­ната на записа и броя на използваните цифри, се постига при основа на бройната система Неперовото число (e = 2,718281828), което е основата на естествените логаритми. Да се работи в система с тази основа, е изключително неудобно, защото това число не може да се представи като отношение на две цели числа. Това ни дава основание да заключим, че оптималната основа на бройната система е 2 или 3. Въпреки, че 3 е по-близо до Неперовото число, то е неподходящо за техническа реализация. Поради тази причина, двоичната бройна система, е единствената подхо­дяща за практическа употреба и тя се използва в съвременните елек­тронноизчислителни машини.

Позиционни бройни системи

Бройните системи се наричат позиционни (positional), тогава, когато мястото (пози­цията) на цифрите има значение за стойността на числото. Това означава, че стойността на цифрата в числото не е строго определена и зависи от това на коя позиция се намира съответната цифра в дадено число. Например в числото 351 цифрата 1 има стойност 1, докато при числото 1024 тя има стойност 1000. Трябва да се отбележи, че основите на бройните системи се прилагат само при позиционните бройни системи. В позиционна бройна система числото A_(p) = (a_(n)a_(n-1)...a₍₀₎,a_(-1)a_(-2)...a_(-k)) може де се представи във вида:

В тази сума T_m има значение на тегловен коефициент за m-тия разряд на числото. В повечето случаи обикновено T_m = P^m, което означава, че:

Образувано по горната сума, числото A_(p) е съставено съответно от цялата си част (a_(n)a_(n-1)...a₍₀₎) и от дробната си част (a_(-1)a_(-2)...a_(-k)), където всяко a принадлежи на множеството от цели числа M={0, 1, 2, ..., p-1}. Лесно се вижда, че при позиционните бройни системи стойността на всеки разряд е по-голяма от стойността на предходния разряд (съседния разряд отдясно, който е по-младши) с толкова пъти, колкото е основата на бройната система. Това обстоятелство, налага при събиране да прибавяме единица към левия (по-старшия) разряд, ако трябва да представим цифра в текущия разряд, която е по-голяма от основата. Системите с основи 2, 8, 10 и 16 са полу­чили по-широко разпространение в изчислителната техника, и в следва­щата таблица е показано съответното представяне на числата от 0 до 15 в тях:

Двоична	Осмична	Десетична	Шестнадесетична
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

Непозиционни бройни системи

Освен позиционни, съществуват и непозиционни бройни системи, при които стойността на всяка цифра е постоянна и не зависи по никакъв начин от нейното място в числото. Като примери за такива бройни системи могат да се посочат съответно римската, гръцката, милетската и др. Като основен недостатък, на непозиционните бройни системи трябва да се посочи това, че чрез тях големите числа се представят неефективно. Заради този си недостатък те са получили по-ограничена употреба. Често това би могло да бъде източник на грешка при определяне на стойността на числата. Съвсем накратко ще разгледаме римската и гръцката бройни системи.

Римска бройна система

Римската бройна система използва следните символи за представяне на числата:

Както вече споменахме, в тази бройна система позицията на цифрата не е от значение за стойността на числото, но за нейното определяне се прилагат следните правила:

1.  Ако две последователно записани римски цифри, са записани така, че стойността на първата е по-голяма или равна на стойността на втората, то техните стойности се събират. Пример:

Числото III=3, а числото MMD=2500.

2.  Ако две последователно записани римски цифри, са в намаляващ ред на стойностите им, то техните стойности се изваждат. Пример:

Числото IX=9, числото XML=1040, а числото MXXIV=1024.

Гръцка бройна система

Гръцката бройна система, е десетична система, при която се извършва групиране по петици. Тя използва следните цифри:

Както се вижда в таблицата, единицата се означава с чертичка, петицата с буквата Г, и степените на 10 с началните букви на съответната гръцка дума.

Следват няколко примера на числа от тази система:

-     ΓΔ = 50 = 5 х 10

-     ΓH = 500 = 5 х 100

-     ΓX = 5000 = 5 х 1 000

-     ΓM = 50 000 =  5 х 10 000

Двоичната бройна система – основа на електронноизчислителната техника

Двоичната бройна система (binary numeral system), е системата, която се използва за представяне и обработка на числата в съвременните електронноизчислителни машини. Главната причина, поради която тя се е наложила толкова широко, се обяснява с обстоятелството, че устройства с две устойчиви състояния се реализират просто, а разходите за производство на двоични аритметични устройства са много ниски.

Двоичните цифри 0 и 1 лесно се представят в изчислителната техника като "има ток" и "няма ток" или като "+5V" и "-5V".

Наред със своите пре­димства, двоичната система за представяне на числата в компютъра си има и недостатъци. Един от големите практически недоста­тъци, е че числата, представени с помощта на тази система са много дълги, т. е. имат голям брой разреди (битове). Това я прави неудобна за непосредствена употреба от човека. За избягване на това неудобство, в практиката се ползват бройни системи с по-големи основи.

Десетични числа

Числата представени в десетична бройна система (decimal numeral system), се задават в първичен вид, т.е. вид удобен за възприемане от човека. Тази бройна система има за основа числото 10. Числата записани в нея са подредени по степените на числото 10. Младшият разряд (първият отдясно на ляво) на десетичните числа се използва за представяне на единиците (10⁰=1), следващият за десетиците (10¹=10), следващият за стотиците (10²=100) и т.н. Казано с други думи, всеки следващ разряд е десет пъти по-голям от предшест­ващия го разряд. Сумата от отделните разряди определя стойността на числото. За пример ще вземем числото 95031, което в десетична бройна система се представя като:

95031 = (9×10⁴) + (5×10³) + (0×10²) + (3×10¹) + (1×10⁰)

Представено в този вид, числото 95031 е записано по естествен за човека начин, защото принципите на десетичната система са възприети като фун­даментални за хората.

Разгледаните подходи важат и за останалите бройни системи. Те имат същата логическа поста­новка, но тя е приложена за бройна система с друга основа. Последното твърдение, се отнася включително и за двоичната и шестнайсетината бройни системи, които ще разгледаме в детайли след малко.

Двоични числа

Числата представени в двоична бройна система, се задават във вторичен вид, т.е. вид удобен за възприемане от изчислителната машина. Този вид е малко по-трудно разбираем за човека. За представянето на двоичните числа, се използва двоичната бройна система, която има за основа числото 2. Числата записани в нея са подредени по степените на двойката. За тяхното представяне, се използват само цифрите 0 и 1.

Прието е, когато едно число се записва в бройна система, различна от десетичната, във вид на индекс в долната му част да се отразява, коя бройна система е използвана за представянето му. Например със записа 1110₍₂₎ означаваме число в двоична бройна система. Ако не бъде указана изрично, бройната система се приема, че е десетична. Числото се произ­нася, като се прочетат последователно неговите цифри, започвайки от ляво на дясно (т.е. прочитаме го от старшия към младшия разряд "бит").

Както и при десетичните числа, гледано от дясно наляво, всяко двоично число изразява степените на числото 2 в съответната последователност. На младшата позиция в двоично число съответства нулевата степен (2⁰=1), на втората позиция съответства първа степен (2¹=2), на третата позиция съответства втора степен (2²=4) и т.н. Ако числото е 8-битово, степените достигат до седма (2⁷=128). Ако числото е 16-битово, степените достигат до петнадесета (2¹⁵=32768). Чрез 8 двоични цифри (0 или 1) могат да се представят общо 256 числа, защото 2⁸=256. Чрез 16 двоични цифри могат да се представят общо 65536 числа, защото 2¹⁶=65536.

Нека дадем един пример за числа в двоична бройна система. Да вземем десетичното число 148. То е съставено от три цифри: 1, 4 и 8, и съответства на следното двоично число:

10010100₍₂₎

148 = (1×2⁷) + (1×2⁴) + (1×2²)

Пълното представяне на това число е изобразено в следващата таблица:

Последователността от осем на брой нули и единици представлява един байт, т.е. това е едно обикновено осем-разрядно двоично число. Чрез един байт могат да се запишат всички числа от 0 до 255 включи­телно. Много често това е не достатъчно и затова се използват по няколко последователни байта за представянето на едно число. Два байта образуват т. н. "машинна дума" (word), която отговаря на 16 бита (при 16-разредните изчислителни машини). Освен нея, в изчислителните машини се използва и т.н. "двойна дума" (double word) или (dword), съответстваща на 32 бита.

Ако едно двоично число завършва на 0, то е четно, а ако завършва на 1, то е нечетно.

Преминаване от двоична в десетична бройна система

При преминаване от двоична в десетична бройна система, се извършва преобразуване на двоичното число в десетично. Всяко число може да се преобразува от една бройна система в друга, като за целта се извършат последователност от действия, които са възможни и в двете бройни системи. Както вече споменахме, числата записани в двоична бройна система се състоят от двоични цифри, които са подредени по степените на двойката. Нека да вземем за пример числото 11001_(2). Преобразуването му в десетично се извършва чрез пресмятането на следната сума:

11001_{(2) =} 1×2⁴ + 1×2³ + 0×2² + 0×2¹ + 1×2⁰ =

=  16₍₁₀₎ + 8₍₁₀₎ + 1₍₁₀₎ = 25₍₁₀₎

От това следва, че 11001₍₂₎ = 25₍₁₀₎

С други думи, всяка една двоична цифра се умножава по 2 на степен, позицията, на която се намира (в двоичното число). Накрая се извършва събиране на числата, получени за всяка от двоичните цифри, за да се получи десетичната равностойност на двоичното число.

Съществува и още един начин за преобразуване, който е известен като схема на Хорнер. При тази схема се извършва умножение на най-лявата цифра по две и събиране със съседната й вдясно. Този резултат се умножава по две и се прибавя следващата съседна цифра от числото (цифрата вдясно). Това продължава до изчерпване на всички цифри в числото, като последната цифра от числото се добавя без умножаване. Ето един пример:

1001₍₂₎ = ((1 × 2 + 0) × 2 + 0) × 2 + 1 = 2 × 2 × 2 + 1 = 9

Преминаване от десетична към двоична бройна система

При преминаване от десетична в двоична бройна система, се извършва преобразуване на десетичното число в двоично. За целите на преобразу­ването се извършва делене на две с остатък. Така се получават частно и остатък, който се отделя.

Отново ще вземем за пример числото 148. То се дели целочислено на основата, към която ще преобразуваме (в примера тя е 2). След това, от остатъците получени при деленето (те са само нули и единици), се записва преобразуваното число. Деленето продължава, докато получим частно нула. Ето пример:

148:2=74 имаме остатък 0;

74:2=37   имаме остатък 0;

37:2=18   имаме остатък 1;

18:2=9     имаме остатък 0;

9:2=4       имаме остатък 1;

4:2=2       имаме остатък 0;

2:2=1       имаме остатък 0;

1:2=0       имаме остатък 1;

След като вече семе извършили деленето, записваме стойностите на остатъците в ред, обратен на тяхното получаване, както следва:

10010100

т.е. 148₍₁₀₎ = 10010100 ₍₂₎

Действия с двоични числа

При двоичните числа за един двоичен разряд са в сила аритметичните правила за събиране, изваждане и умножение:

0 + 0 = 0                      0 - 0 = 0                           0 × 0 = 0

1 + 0 = 1                      1 - 0 = 1                           1 × 0 = 0

0 + 1 = 1                      1 - 1 = 0                           0 × 1 = 0

1 + 1 = 10                    10 - 1 = 1                         1 × 1 = 1

С двоичните числа могат да се извършват и логически действия, като логическо умножение (конюнкция), логическо събиране (дизюнкция) и сума по модул две (изключващо или).

Трябва да се отбележи, че при извършване на аритметични действия над многоразредни числа трябва да се отчита връзката между отделните разреди чрез пренос или заем, когато извършваме съответно събиране или изваждане. Да разгледаме някои детайли относно побитовите оператори.

Побитово "и"

Побитов AND оператор – може да се използва за проверка на стойност на даден бит в число. Например, ако искаме да проверим дали дадено число е четно (проверяваме дали най-младшият бит е 1):

10111011 AND 00000001 = 00000001

Резултатът е 1 и това означава, че числото е нечетно (ако резултатът беше 0, значи е четно).

В C# побитовото "и" се означава с & и се използва така:

Побитово "или"

Побитов OR оператор – може да се ползва, ако например искаме да "вдигнем" даден бит в 1:

10111011 OR 00000100 = 10111111

Означението на побитовото "или" в C# e | и се използва така:

Побитово "изключващо и"

Побитов XOR оператор – всяка двоична цифра се обработва поотделно, като когато имаме 0 във втория операнд, стойността на същия бит от първия се копира в резултата. Където имаме 1 във втория операнд, там обръщаме стойността от съответната позиция на първия и записваме в резултата:

10111011 XOR 01010101 = 11101110

В C# означението на оператора "изключващо или" е ^:

Побитово отрицание

Побитов NOT оператор – това е унарен (unary) оператор, което означава, че се прилага върху един единствен операнд. Това, което прави е да обърне всеки бит от дадено двоично число в обратната стойност:

NOT 10111011 = 01000100

В C# побитовото отрицание се отбелязва с ~:

Шестнайсетични числа

При шестнайсетичните числа (hexadecimal numbers) имаме за основа на бройната система числото 16, което налага да бъдат използвани 16 знака (цифри) за представянето на всички възможни стойности от 0 до 15 включително. Както вече беше показано в една от таблиците в предходните точки, за представянето на шестнайсе­тичните числа се използват числата от 0 до 9 и латинските букви от A до F. Всяка от тях има съответната стойност:

A=10, B=11, C=12, D=13, E=14, F=15

Като примери за шестнайсетични числа могат да бъдат посочени съответно, D2, 1F2F1, D1E и др.

Преминаването към десетична система става като се умножи по 16⁰ стойността на най-дясната цифра, по 16¹ следващата вляво, по 16² следващата вляво и т.н. и накрая се съберат. Например:

D1E₍₁₆₎ = Е*16⁰ + 1*16¹ + D*16² = 14*1 + 1*16 + 13*256 = 3358₍₁₀₎.

Преминаването от десетична към шестнайсетична бройна система става като се дели десетичното число на 16 и се вземат остатъците в обратен ред. Например:

3358 / 16 = 209 + остатък 14 (Е)

209 / 16 = 13 + остатък 1 (1)

13 / 16 = 0 + остатък 13 (D)

          Взимаме остатъците в обратен ред и получаваме числото D1E₍₁₆₎.

Бързо преминаване от двоични към шестнайсетични числа

Бързото преобразуване, от двоични в шестнайсетични числа се извършва бързо и лесно, чрез разделяне на двоичното число на групи от по четири бита (разделяне на полубайтове). Ако броят на цифрите в числото не е кратен на четири, то се добавят водещи нули в старшите разряди. След разделянето и евентуалното добавяне на нули, се заместват всички полу­чени групи със съответстващите им цифри. Ето един пример:

Нека да ни е дадено следното число: 1110011110₍₂₎.

1.  Разделяме го на полубайтове и добавяме водещи нули

Пример: 0011 1001 1110.

2.  Заместваме всеки полубайт със съответната шестнайсетична цифра и така получаваме 39E₍₁₆₎.

Следователно 1110011110 ₍₂₎ = 39E₍₁₆₎.

Бройни системи – обобщение

Като обобщение ще формулираме отново, в кратък, но ясен вид алгоритмите за преминаване от една позиционна бройна система в друга:

-     Преминаването от десетична в k-ична бройна система се извършва като последователно се дели десетичното число на основата на новата система k и получените остатъци (съответстващата им k-ична цифра) се натрупват в обратен ред.

-     Преминаването от k-ична бройна система към десетична се извършва като се умножи последната цифра на k-ичното число по k⁰, предпос­ледната – по k¹, следващата – по k² и т.н. и получените произведе­ния се сумират.

-     Преминаването от k-ична бройна система към p-ична се извършва чрез междинно преминаване към десетична бройна система (с изключение на случая шестнайсетична / двоична бройна система).

Представяне на числата

За съхраняване на данните в оперативната памет на електронноиз­чис­лителните машини се използва двоичен код. В зависимост от това какви данни съхраняваме (символи, цели или реални числа с цяла и дробна част) информацията се представя по различен начин. Този начин се опре­деля от типа на данните.

Дори и програмистът на език от високо ниво трябва да знае, какъв вид имат данните разположени в оперативната памет на машината. Това се отнася, и за случаите, когато данните се намират на външен носител, защото при обработката им те се разполагат в оперативната памет.

В настоящата секция са разгледани начините за представяне и обработка на различни типове данни. Най-общо те се основават на понятията бит, байт и машинна дума.

Бит е една двоична единица от информация, със стойност 0 или 1.

Информацията в паметта се групира в последовател­ности от 8 бита, които образуват един байт.

За да бъдат обработени от аритметичното устройство, данните се пред­ставят в паметта от определен брой байтове (2, 4 или 8), които образуват машинната дума. Това са концепции, които всеки програмист трябва задължи­телно да знае и разбира.

Представяне на цели числа в паметта

Едно от нещата, на които до сега не обърнахме внимание, е знакът на числата. Представянето на целите числа в паметта на компютъра може да се извърши по два начина: със знак или без знак. Когато числата се представят със знак се въвежда знаков разред. Той е най-старшият разред и има стойност 1 за отрицателните числа и 0 за положителните. Останалите разреди са информационни и отразяват (съдържат) стойността на числото. В случая на числа без знак всички битове се използват за записване на стойността на числото.

Цели числа без знак

За целите числа без знак (unsigned integers) се заделят по 1, 2, 4 или 8 байта от паметта. В зависимост, от броя на байтовете използвани при представянето на едно число, се образуват обхвати на представяне с различна големина. Посред­ством n на брой бита могат да се представят цели числа без знак в обхвата [0, 2ⁿ-1]. Следващата таблица, показва обхватa от стойности на целите числа без знак:

Ще покажем пример при еднобайтово и двубайтово представяне на числото 158, което се записва в двоичен вид като 10011110₍₂₎:

1. Представяне с 1 байт:

2. Представяне с 2 байта:

Представяне на отрицателни числа

За отрицателните числа се заделят по 1, 2, 4 или 8 байта от паметта на компютъра, като най-старшият разред (най-левия бит) има значение на знаков и носи информация за знака на числото. Както вече споменахме, когато знаковият бит има стойност 1 числото е отрицателно, а в противен случай е положително.

Следващата таблица, показва обхвата от стойно­сти на целите числа със знак в компютърната техника според броя байтове, използвани за запис­ването им:

За кодирането на отрицателните числа, се използват прав, обратен и допълнителен код. И при трите представяния целите числа със знак са в границите: [-2^n-1, 2^n-1-1]. Положителните числа винаги се представят по един и същи начин и за тях правият, обратният и допълнителният код съвпадат.

Правият код (signed magnitude) е най-простото представяне на числото. Старшият бит е знаков, а в оставащите битове е записана абсолютната стойност на числото. Ето няколко примера:

Числото 3 в прав код се представя в осембитово число като 00000011.

Числото -3 в прав код се представя в осембитово число като 10000011.

Обратният код (one's complement) се образува от правия код на числото, чрез инвертиране (заместване на всички нули с единици и единици с нули). Този код не е никак удобен за извършването на аритметичните действия събиране и изваждане, защото се изпълнява по различен начин, когато се налага изваждане на числа. Освен това се налага знаковите битове да се обра­ботват отделно от информационните. Този недостатък се избягва с употре­бата на допълнителен код, при който вместо изваждане се извършва събиране с отрицателно число. Последното е представено чрез неговото допълнение, т.е. разликата между 2ⁿ и самото число. Пример:

Числото -127 в прав код се представя като 1 1111111, а в обратен код като 1 0000000.

Числото 3 в прав код се представя като 0 0000011, а в обратен код има вида 0 1111100.

Допълнителният код (two's complement) е число в обратен код, към което е прибавена (чрез събиране) единица. Пример:

Числото -127 представено в допълнителен код има вида 1 0000001.

При двоично-десетичния код, известен е още като BCD код (Binary Coded Decimal) в един байт се записват по две десетични цифри. Това се постига, като чрез всеки полубайт се кодира една десетична цифра. Числа представени чрез този код могат да се пакетират, т.е. да се представят в пакетиран формат. Ако представим една десетична цифра в един байт се получава непакетиран формат.

Съвременните микропроцесори използват един или няколко от разгле­даните кодове за представяне на отрицателните числа, като най-разпро­страненият начин е представянето в допълнителен код.

Целочислени типове в C#

В C# има осем целочислени типа данни със знак и без знак. В зависимост от броя байтове, които се заделят в паметта за тези типове, се определя и съответният диапазон от стойности, които те могат да заемат. Следват описания на типовете:

Ще разгледаме накратко най-използваните типове. Най-широко използва­ният целочис­лен тип е int. Той се представя като 32-битово число в допълнителен код и приема стойности в интервала [-2³¹, 2³¹-1]. Промен­ливите от този тип най-често се използват за управление на цикли, индексиране на масиви и други целочислени изчисления. В следващата таблица е даден пример за декларация на променлива от тип int:

int integerValue = 25; int integerHexValue = 0x002A; int y = Convert.ToInt32("1001", 2); // Converts binary to int

Типът long е най-големият целочислен тип със знак в C#. Той има размерност 64 бита (8 байта). При присвояване на стойности на промен­ливите от тип long се използват латинските букви "l" или "L", които се поставят в края на целочисления литерал. Поставен на това място, този модификатор означава, че литералът има стойност от тип long. Това се прави, защото по подразбиране целочислените литерали са от тип int. В следващия пример декларираме и присвояваме 64-битови цели числа на променливи от тип long:

long longValue = 9223372036854775807L; long newLongValue = 932145699054323689l;

Важно условие е да се внимава да не бъде надхвърлен обхватът на представимите числа и за двата типа. Все пак C# предоставя възможността да контролираме какво се случва когато настъпи препълване. Това става посредством checked и unchecked блоковете. Първите се използват когато е нужно приложението да хвърли изключение (от тип System. OverflowException) в случай на надхвърляне на обхвата на променли­вата. Следният програмен код прави именно това:

checked {           int a = int.MaxValue;           a = a + 1;           Console.WriteLine(a); }

В случай че фрагментът е в unchecked блок, изключение не се хвърля и изведеният резултат е неверен:

-2147483648

По подразбиране, в случай че не се използват тези блокове C# компилаторът работи в unchecked режим.

C# включва и типове без знак, които могат да бъдат полезни при нужда от по-голям обхват на променливите в диапазона на положителните числа. По-долу са няколко примера за деклариране на променливи без знак. Обърнете внимание на суфиксите за ulong (всякакви комбинации от U, L, u, l).

byte count = 50; ushort pixels = 62872; uint points = 4139276850; // or 4139276850u, 4139276850U ulong y = 18446744073709551615; // or UL, ul, Ul, uL, Lu, lU

Представянията Big-Endian и Little-Endian

При цели числа, които се записват в повече от един байт, има два варианта за наредба на байтовете в паметта:

-     Little-Endian (LE) – байтовете се подреждат от ляво надясно от най-младшия към най-старшия. Това представяне се използва при Intel x86 и Intel x64 микропроцесорните архитектури.

-     Big-Endian (BE) – байтовете се подреждат от ляво надясно от най-старшия към най-младшия. Това представяне се използва при PowerPC, SPARC и ARM микропроцесорните архитектури.

Ето един пример: числото A8B6EA72₍₁₆₎ се представя в двете наредби на байтовете по следния начин:

Има някои класове в C#, които предоставят възможности за дефиниране на това кой стандарт за подредба на байтовете да се използва. Това е важно при операции от като изпращане / приемане на потоци от инфор­мация по мрежата и други видове комуникация между устройства, произ­ведени по различни стандарти. Полето IsLittleEndian на BitConverter класа например показва в какъв режим класът работи и как се съхраняват данните за текущата компютърна архитектура.

Представяне на реални числа с плаваща запетая

Реалните числа са съставени от цяла и дробна част. В компютърната техника, те се представят като числа с плаваща запетая (floating-point numbers). Всъщност това представяне идва от възприетия от водещите производи­тели на микропроцесори Standard for Floating-Point Arithmetic (IEEE 754). Повечето хардуерни плат­форми и езици за програмиране позволяват или изискват изчисленията да се извършват съгласно изискванията на този стандарт. Стандартът определя:

-     Аритметични формати: набор от двоични и десетични данни с плаваща запетая, които са съставени от краен брой цифри.

-     Формати за обмен: кодировки (битови низове), които могат да бъдат използвани за обмен на данни в една ефективна и компактна форма.

-     Алгоритми за закръгляване: методи, които се използват за закръг­ляване на числата по време на изчисления.

-     Операции: аритметика и други операции на аритметичните формати.

-     Изключения: представляват сигнали за извънредни случаи като деление на нула, препълване и др.

Съгласно IEEE-754 стандарта произволно реално число R може да бъде представено във вида:

R = M * q^p

където M e мантисата на числото, а p е порядъкът му (експонента), и съответно q е основа на бройната система, в която е представено числото. Мантисата трябва да бъде положителна или отрицателна правилна дроб, т.е. |M|<1, а порядъкът – положително или отрицателно цяло число.

При посочения начин на представяне на числата, всяко число във формат с плаваща запетая, ще има следния обобщен вид ±0,M*q^±p.

В частност, когато представяме числата във формат с плаваща запетая чрез двоична бройна система, ще имаме R = M * 2^p. При това представя­не на реалните числа в паметта на компютъра, след промяна на порядъка се стига и до изместване "плаване" на десетичната запетая в мантисата. Форматът на представянето с плаваща запетая има полулогаритмична форма. Той е изобразен нагледно на следващата фигура:

Представяне на числа с плаваща запетая – пример

Нека дадем един пример за представяне на число с плаваща запетая в паметта. Искаме да запишем числото -21,15625 в 32-битов (single precision) floating-point формат по стандарта IEEE-754. При този формат се използват 23 бита за мантиса, 8 бита за експонента и 1 бит за знак на числото. Представянето на числото е следното:

Знакът на числото е отрицателен, т. е. мантисата има отрицателен знак:

S = -1

Порядъкът (експонентата) има стойност 4 (записана с изместен порядък):

p = (2⁰ + 2¹ + 2⁷) - 127 = (1+2+128) – 127 = 4

За преминаване към истинската стойност изваждаме 127 от стойността на допълнителния код, защото работим с 8 бита (127 = 2⁸-1).

Мантисата има следната стойност (без да взимаме предвид знака):

М    = 1 + 2^-2 + 2^-4 + 2^-7 + 2^-9 =

= 1 + 0,25 + 0,0625 + 0,0078125 + 0,001953125 =

= 1,322265625

Забелязахте ли, че добавихме единица, която липсва в двоичния запис на мантисата? Това е така, защото мантисата винаги е нормализирана и започва с единица, която се подразбира.

Стойността на числото се изчислява по формулата R = M * 2^p, която в нашия пример добива вида:

R = -1,3222656 * 2⁴ = -1,322265625 * 16 = -21,1562496 ≈ -21,15625

Нормализация на мантисата

За по-пълното използване на разрядната решетка мантисата трябва да съдържа единица в най-старшия си разред. Всяка мантиса удовлетворя­ваща това условие са нарича нормализи­рана. При IEEE-754 стандарта едини­цата в цялата част на мантисата се подразбира, т.е. мантисата е винаги число между 1 и 2.

Ако по време на изчисленията се достигне до резултат, който не удовлет­ворява това условие, то имаме нарушение на нормализа­цията. Това изисква, преди да се пристъпи към по-нататъшна обработка на числото то да бъде нормализирано, като за целта се измества запетаята в мантисата и след това се извършва съответна промяна на порядъка.

Типовете float и double в C#

В C# разполагаме с два типа данни за представяне на числата с плаваща запетая. Типът float е 32-битово реално число с плаваща запетая, за което е прието да се казва, че има единична точност (single precision floating-point number). Типът double е 64-битово реално число с плаваща запетая, за което е прието да се казва, че има двойна точност (double precision floating-point number). Тези реални типове данни и аритметич­ните операции върху тях съответстват на спецификацията, определена от стандарта IEEE 754-1985. В следната таблица са по-важните характерис­тики на двата типа:

При тип float имаме мантиса, която съхранява 7 значещи цифри, докато при тип double тя съхранява 15-16 значещи цифри. Останалите битове се използват за задаването на знаците на мантисата и стойността на порядъка. Типът double освен с по-голям брой значещи цифри разпо­лага и с по-голям порядък, т.е. обхват на приеманите стойности. Ето един пример за декларация на променливи от тип float и тип double:

float total = 5.0f; float result = 5.0f; double sum = 10.0; double div = 35.4 / 3.0; double x = 5d;

Суфиксите, поставени след числата от дясната страна на равенството са с цел те да бъдат третирани като числа от съответен тип (f за float, d за double). В случая са поставени, тъй като по подразбиране 5.0 ще се интерпретира от тип double, а 5 – от тип int.

В C# по подразбиране числата с плаваща запетая, въве­дени като литерал са от тип double.

Целочислени и числа с плаваща запетая могат да присъстват в даден израз. В такъв случай целочислените променливи биват конвертирани към такива с плаваща запетая и резултатът се получава по следните правила:

1.  Ако някои от типовете с плаваща запетая е double, резултатът е от тип double (или bool).

2.  Ако няма double тип в израза, резултатът е от тип float (или bool).

Много от математическите операции могат да дадат резултати, които нямат конкретна числена стойност като например стойността "+/- без­крайност" или стойността NaN (което означава "Not a Number"), които не представляват числа. Ето един пример:

double d = 0; Console.WriteLine(d); Console.WriteLine(1/d); Console.WriteLine(-1/d); Console.WriteLine(d/d);

Ако го изпълним, ще получим следния резултат:

0.0 Infinity -Infinity NaN

Ако изпълним горния код с тип int вместо double, ще получим System.DivideByZeroException, защото целочисленото деление на 0 е непозволена операция.

Грешки при числата с плаваща запетая

Числата с плаваща запетая (представени съгласно стандарта IEEE 754) са удобни за работа с изчисления от физиката, където се използват много големи числа (с няколко стотици цифри) и много близки до нулата числа (със стотици цифри след десетичната запетая преди първата значеща цифра). При такива числа форматът IEEE 754 е изключително удобен, защото запазва порядъка на числото в експонентата, а мантисата се ползва само за съхранение на значещите цифри. При 64-битови числа с плаваща запетая се постига точност до 15-16 цифри и експонента отместваща десетичната точка над 300 позиции наляво и надясно.

За съжаление не всяко реално число има точно представяне във формат IEEE 754, тъй като не всяко число може да се представи като полином на ограничен брой събираеми, които са отрицателни степени на двойката. Това важи с пълна сила дори за числата, които употребяваме ежедневно при най-простите финансови изчисления. Например числото 0.1 записано като в 32-битова floating-point стойност се представя като 0.099999994. Ако се ползва подходящо закръгляне, числото се възприема като 0.1, но грешката може да се натрупа и да даде сериозни отклонения, особено при финансови изчисления. Например при сумиране на 1000 артикула с единична цена от по 0.1 EUR би трябвало да се получи сума 100 EUR, но ако смятаме с 32-битови floating-point числа, ще получим сумата 99.99905. Ето реален пример на C# в действие, който доказва грешките причинени от неточното представяне на десетичните реални числа в двоична бройна система:

float sum = 0f; for (int i = 0; i < 1000; i++) {       sum += 0.1f; } Console.WriteLine("Sum = {0}", sum); // Sum = 99.99905

Можете сами да се убедите в грешките при подобни пресмятания като изпълните примера или си поиграете с него и го модифицирате, за да получите още по-фрапантни грешки.

Точност на числата с плаваща запетая

Точността на резултатите от изчисленията при работа с числа с плаваща запетая зависят от следните параметри:

1.  Точността на представяне на числата.

2.  Точността на използваните числени методи.

3.  Стойностите на грешките, получени при закръгляване и др.

Поради това, че числата се представят в паметта с някаква точност, при изчисленията върху тях резултатите могат също да са неточни. Нека като пример да разгледаме следния програмен фрагмент:

double sum = 0.0;       for (int i = 1; i <= 10; i++) {           sum += 0.1; } Console.WriteLine("{0:r}", sum); Console.WriteLine(sum);

По време на неговото изпълнение, в цикъл добавяме стойността 1/10 в променливата sum. В извикването на метода WriteLine() използваме round-trip format спецификаторът "{0:r}" за да изведем точната (неза­кръглена) стойност която се съдържа в променливата, а след това отпе­чатваме същата стойност без да указваме формат. Очаква се, че при изпълнението на тази програма ще получим резултат 1.0, но в действи­телност, когато закръглянето е изключено програмата извежда стой­ност, много близка до вярната, но все пак различна:

0.99999999999999989 1

Както се вижда от примера, по подразбиране при отпечатване на floating-point числа в .NET Framework те се закръглят и така привидно се намаляват грешките от неточното им представяне във формата IEEE 754. Резултатът от горното изчисление, както се вижда, е грешен, но след закръгляне изглежда правилен. Ако обаче съберем 0.1 няколко хиляди пъти, грешката ще се натрупа и закръгляването не може да я компенсира.

Причината за грешния резултат в примера е, че числото 0.1 няма точно представяне в типа double и се представя със закръгляне. Нека заменим double с float:

float sum = 0.0f;       for (int i = 1; i <= 10; i++) {           sum += 0.1f; } Console.WriteLine("{0:r}", sum);

Ако изпълним горния код ще получим съвсем друга сума:

1.00000012

Причината за това отново е закръглянето.

Ако направим разследване защо се получават тези резултати, ще се убедим, че числото 0.1 се представя в типа float по следния начин:

Всичко изглежда коректно с изключение на мантисата, която има стойност, малко по-голяма от 1.6, а не точно 1.6, защото това число не може да се представи като сума от отрицателни степени на 2. Ако трябва да сме съвсем точни, стойността на мантисата е 1 + 1 / 2 + 1 / 16 + 1 / 32 + 1 / 256 + 1 / 512 + 1 / 4096 + 1 / 8192 + 1 / 65536 + 1 / 131072 + 1 / 1048576 + 1 / 2097152 + 1 / 8388608 ≈ 1,60000002384185791015625 ≈ 1.6. Така числото 0.1 в крайна сметка се представя във формат IEE 754 като съвсем малко повече от 1.6 × 2^-4 и грешката настъпва не при събирането, а още преди това – при запис­ването на 0.1 в типа float.

Типовете double и float имат поле Epsilon, което е константа и съдържа най-малката стойност по-голяма от 0, която съответно System.Single или System.Double инстанцията може да представи. Всяка стойност по-малка от Epsilon се счита за равна на 0. Така например, ако сравняваме две числа, които са все пак различни, но тяхната разлика е по-малка от Epsilon, то те ще бъдат сметнати за равни.

Типът decimal

Типът System.Decimal в .NET Framework използва десетична аритме­тика с плаваща запетая (decimal floating-point arithmetic) и 128-битова точност, която е подходяща за големи и прецизни финансови изчисления. Ето и някои характеристики на типа decimal:

За разлика от числата с плаваща запетая, типът decimal запазва точност за всички десетични числа, които са му в обхвата. Тайната за тази отлична точност при работа с десетични числа се крие във факта, че вътрешното представяне на мантисата не е в двоична бройна система, а в десетична. Експонентата му също е степен на 10, а не на 2. Така не се налага приближено представяне на десетичните числа – те се записват точно, без преобразуване в двоична бройна система.

Тъй като типовете float и double и операциите върху тях се реализират хардуерно от аритметичния копроцесор, който е част от всички съвре­менни компютърни микропроцесори, а decimal се реализира софтуерно, типът decimal е няколко десетки пъти по-бавен от double, но е незаменим при изпълнението на финансови изчисления.

В случай, че целим да присвоим даден литерал на променлива от тип decimal, е нужно да използваме суфиксите m или M. Например:

decimal calc = 20.4m; decimal result = 5.0M;

Нека използваме decimal вместо float / double в примера, който разгледахме преди малко:

decimal sum = 0.0m; for (int i = 1; i <= 10000000; i++) {           sum += 0.0000001m; } Console.WriteLine(sum);

Резултатът този път е точно такъв, какъвто се очаква да бъде:

1.0000000

Въпреки че decimal типът има по-голяма точност, от типовете с плаваща запетая, той предоставя по-малък обхват на стойности и не може напри­мер да запише стойността 1e-50. Така, при конвер­тиране на числа с плаваща запетая към decimal, може да се получат грешки от препълване.

Символни данни (стрингове)

Символните (текстовите) данни в компютърната техника представляват текст, кодиран чрез поредици от байтове. Има различни схеми за коди­ране на текстови данни. Повечето от тях кодират един символ с един байт или с поредица от няколко байта. Такива са кодиращите схеми ASCII, Windows-1251, UTF-8 и UTF-16.

Кодиращи схеми (encodings)

Кодиращата схема ASCII съпоставя уникален номер на буквите от латин­ската азбука и някои други символи и специални знаци и ги записва в един байт. ASCII стандартът съдържа общо 127 символа, всеки от които се записва в 1 байт. Текст, записан като поредица от байтове по стандарта ASCII не може да съдържа кирилица и символи от други азбуки като арабската, корейската и китайската.

По подобие на ASCII стандарта кодиращата схема Windows-1251 съпо­ставя на буквите от латинската азбука, кирилицата и някои други символи и специални знаци по един байт. Кодирането Windows-1251 дефинира номера на общо 256 символа – точно колкото са различните стойности, които могат да се запишат с един байт. Текст, записан по стандарта Windows-1251 може да съдържа кирилица и латиница, но не може да съдържа арабски, индийски и китайски символи.

Кодирането UTF-8 е съвсем различно. В него могат да бъдат записани всички символи от Unicode стандарта – буквите и знаците, използвани във всички масово разпространени езици по света (кирилица, латиница, арабски, китайски, японски, корейски и много други азбуки и писмени системи). Кодирането UTF-8 съдържа над половин милион символа. При UTF-8 по-често използваните символи се кодират в 1 байт (например латиницата), по-рядко използваните символи се кодират в 2 байта (например кирилицата) и още по-рядко използваните символи се кодират с 3 или 4 байта (например китайската, японската и корейската азбука).

Кодирането UTF-16, подобно на UTF-8 може да представи текстове от всички по-масово използвани по света езици и писмени системи, описани в Unicode стандарта. При UTF-16 всеки символ се записва в 16 бита, т.е. в 2 байта, а някои по-рядко използвани символи се представят като поре­дица от две 16-битови стойности.

Представяне на поредици от символи

Поредиците от символи могат да се представят по-няколко начина. Най-разпространеният начин за записване на текст в паметта на компютъра е в 2 или 4 байта да се запише дължината на текста, следван от поредица от байтове, които представят самия текст в някакво кодиране (например Windows-1251 или UTF-8).

Друг, по-малко разпространен начин за записване на текстове в паметта, типичен за езика C, представя текстовете чрез поредица от символи, най-често в еднобайтово кодиране, следвани от специален завършващ символ, най-често с код 0. Така дължината на текста, записан на дадена позиция в паметта, не е предварително известна, което се счита за сериозен недостатък в много ситуации.

Типът char

Типът char в езика C# представлява 16-битова стойност, в която е кодиран един Unicode символ или част от Unicode символ. При повечето азбуки (например използваните от всички европейски езици) една буква се записва в една 16-битова стойност и по тази причина обикновено се счита, че една променлива от тип char представя един символ. Ето един пример:

char ch = 'A'; Console.WriteLine(ch);

Типът string

Типът string в C# съдържа текст, кодиран в UTF-16. Един стринг в C# се състои от 4 байта дължина и поредица от символи, записани като 16-битови стойности от тип char. В типа string може да се запишат текстове на всички широко разпространени азбуки и писмени системи от човешк­ите езици – латиница, кирилица, китайски, японски, арабски и много, много други. Ето един пример за използване на типа string:

string str = "Example"; Console.WriteLine(str);

Упражнения

1.    Превърнете числата 151, 35, 43, 251 и -0,41 в двоична бройна система.

2.    Превърнете числото 1111010110011110₍₂₎ в шестнадесетична и в десе­тична бройна система.

3.    Превърнете шестнайсетичните числа 2A3E, FA, FFFF, 5A0E9 в двоична и десетична бройна система.

4.    Да се напише програма, която преобразува десетично число в дво­ично.

5.    Да се напише програма, която преобразува двоично число в десе­тично.

6.    Да се напише програма, която преобразува десетично число в шестнадесетично.

7.    Да се напише програма, която преобразува шестнадесетично число в десетично.

8.    Да се напише програма, която преобразува шестнадесетично число в двоично.

9.    Да се напише програма, която преобразува двоично число в шестна­десетично.

10. Да се напише програма, която преобразува двоично число в десетично по схемата на Хорнер.

11. Да се напише програма, която преобразува римските числа в арабски.

12. Да се напише програма, която преобразува арабските числа в римски.

13. Да се напише програма, която по зададени N, S, D (2 ≤ S, D ≥ 16) преобразува числото N от бройна система с основа S към бройна система с основа D.

14. Да се напише програма, която по дадено цяло число извежда на конзолата двоичното представяне на числото.

15. Опитайте да сумирате 50 000 000 пъти числото 0.000001. Използвайте цикъл и събиране (не директно умножение). Опитайте с типовете float и double и след това с decimal. Забелязвате ли разликата в резултатите и в скоростта?

16. * Да се напише програма, която отпечатва стойността на мантисата, знака на мантисата и стойността на експонентата за числа тип float (32-битови числа с плаваща запетая съгласно стандарта IEEE 754). Пример: за числото -27,25 да се отпечата: знак = 1, експонента = 10000011, мантиса = 10110100000000000000000.

Решения и упътвания

1.    Използвайте методите за превръщане от една бройна система в друга. Можете да сверите резултатите си с калкулатора на Windows, който поддържа работа с бройни системи след превключване в режим "Scientific".

2.    Погледнете упътването за предходната задача.

3.    Погледнете упътването за предходната задача.

4.    Правилото е "делим на 2 и долепяме остатъците в обратен ред". За делене с остатък използваме оператора %.

5.    Започнете от сума 0. Умножете най-десния бит с 1 и го прибавете към сумата. Следващия бит вляво умножете по 2 и добавете към сумата. Следващия бит отляво умножете по 4 и добавете към сумата и т.н.

6.    Правилото е "делим на основата на системата (16) и долепяме остатъ­ците в обратен ред". Трябва да си напишем логика за отпечатване на шестнайсетична цифра по дадена стойност между 0 и 15.

7.    Започнете от сума 0. Умножете най-дясната цифра с 1 и я прибавете към сумата. Следващата цифра вляво умножете по 16 и я добавете към сумата. Следващата цифра вляво умножете по 16*16 и я добавете към сумата и т.н. до най-лявата шестнайсетична цифра.

8.    Ползвайте бързия начин за преминаване между шестнайсетична и двоична бройна система (всяка шестнайсетична цифра съответства на 4 двоични бита).

9.    Ползвайте бързия начин за преминаване между двоична и шестнайсе­тична бройна система (всяка шестнайсетична цифра съответства на 4 двоични бита).

10. Приложете директно схемата на Хорнер.

11. Сканирайте цифрите на римското число отляво надясно и ги добавяйте към сума, която първоначално е инициализирана с 0. При обработката на всяка римска цифра я взимайте с положителен или отрицателен знак в зависимост от следващата цифра (дали има по-малка или по-голяма десетична стойност).

12. Разгледайте съответствията на числата от 1 до 9 с тяхното римско представяне с цифрите "I", "V" и "X":

1 -> I

2 -> II

3 -> III

4 -> IV

5 -> V

6 -> VI

7 -> VII

8 -> VIII

9 -> IX

Имаме абсолютно аналогични съответствия на числата 10, 20, ..., 90 с тяхното представяне с римските цифри "X", "L" и "C", нали? Имаме аналогични съответствия между числата 100, 200, ..., 900 и тяхното представяне с римските цифри "C", "D" и "M" и т.н.

Сега сме готови да преобразуваме числото N в римска бройна система. То трябва да е в интервала [1...3999], иначе съобщаваме за грешка. Първо отделяме хилядите (N / 1000) и ги заместваме с римския им еквивалент. След това отделяме стотиците ((N / 100) % 10) и ги заместваме с римския им еквивалент и т.н.

13. Можете да прехвърлите числото от бройна система с онова S към бройна система с онова 10, а после от бройна система с основа 10 към бройна система с онова D.

14. За задачата можете да използвате резултата от операцията %2 (остатък при деление с 2).

15. Ако изпълните правилно изчисленията, ще получите съответно 32 (за float), 49.9999999657788 (за double) и 50 (за decimal). Като скорост ще установите, че събирането на decimal стойности е поне 10 пъти по-бавно от събирането на double стойности.

16. Използвайте специалният метод за представяне на числа с плаваща запетая с двойна точност като 64 битово цяло число System. BitConverter.DoubleToInt64Bits(<double>), след което използвайте подходящи побитови операции (измествания и битови маски).

Дискусионен форум

Коментирайте книгата и задачите в нея във: форума на софтуерната академия.