Глава 7. Масиви
В тази тема...
В настоящата тема ще се запознаем с масивите като средство за обработка на поредица от еднакви по тип елементи. Ще обясним какво представляват масивите, как можем да декларираме, създаваме, инициализираме и използваме масиви. Ще обърнем внимание на едномерните и многомерните масиви. Ще разгледаме различни начини за обхождане на масив, четене от стандартния вход и отпечатване на стандартния изход. Ще дадем много примери за задачи, които се решават с използването на масиви и ще демонстрираме колко полезни са те.
Съдържание
- Видео
- Презентация
- Мисловни карти
- Какво е "масив"?
- Деклариране и заделяне на масиви
- Достъп до елементите на масив
- Четене на масив от конзолата
- Отпечатване на масив на конзолата
- Итерация по елементите на масив
- Многомерни масиви
- Масиви от масиви
- Упражнения
- Решения и упътвания
- Демонстрации (сорс код)
- Дискусионен форум
Видео
Презентация
Мисловни карти
Какво е "масив"?
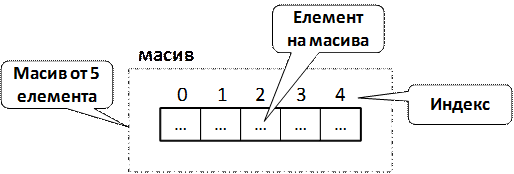
Масивите са неизменна част от повечето езици за програмиране. Те представляват съвкупности от променливи, които наричаме елементи:
Елементите на масивите в C# са номерирани с числата 0, 1, 2, ... N-1. Тези номера на елементи се наричат индекси. Броят елементи в даден масив се нарича дължина на масива.
Всички елементи на даден масив са от един и същи тип, независимо дали е примитивен или референтен. Това ни помага да представим група от еднородни елементи като подредена свързана последователност и да ги обработваме като едно цяло.
Масивите могат да бъдат от различни размерности, като най-често използвани са едномерните и двумерните масиви. Едномерните масиви се наричат още вектори, а двумерните – матрици.
Деклариране и заделяне на масиви
В C# масивите имат фиксирана дължина, която се указва при инициализирането им и определя броя на елементите им. След като веднъж е зададена дължината на масив при неговото създаване, след това не е възможно да се променя.
Деклариране на масив
Масиви в C# декларираме по следния начин:
|
int[] myArray; |
В примера променливата myArray е името на масива, който е от тип (int[]), т.е. декларирали сме масив от цели числа. С [] се обозначава, че променливата, която декларираме е масив от елементи, а не единичен елемент.
При декларация на променливата от тип масив, тя представлява референция (reference), която няма стойност (сочи към null), тъй като още не е заделена памет за елементите на масива.
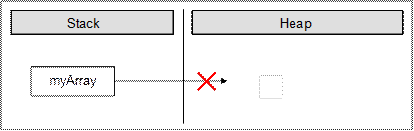
Ето как изглежда една променлива от тип масив, която е декларирана, но още не е заделена памет за елементите на масива:
В стека за изпълнение на програмата се заделя променлива с име myArray и в нея се поставя стойност null (липса на стойност).
Създаване (заделяне) на масив – оператор new
В C# масив се създава с ключовата дума new, която служи за заделяне (алокиране) на памет:
|
int[] myArray = new int[6]; |
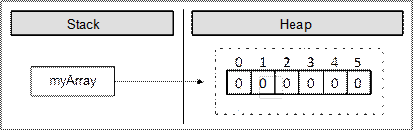
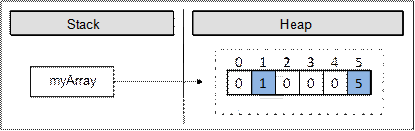
В примера заделяме масив с размер 6 елемента от целочисления тип int. Това означава, че в динамичната памет (heap) се заделя участък от 6 последователни цели числа, които се инициализират със стойност 0:
Картинката показва, че след заделянето на масива променливата myArray сочи към адрес в динамичната памет, където се намира нейната стойност. Елементите на масивите винаги се съхраняват в динамичната памет (в т. нар. heap).
При заделянето на масив в квадратните скоби се задава броят на елементите му (цяло неотрицателно число) и така се фиксира неговата дължина. Типът на елементите се пише след new, за да се укаже за какви точно елементи трябва да се задели памет.
Инициализация на масив. Стойности по подразбиране
Преди да използваме елемент от даден масив той трябва да има начална стойност. В някои езици за програмиране не се задават начални стойности по подразбиране, и тогава при опит за достъпване на даден елемент може да възникне грешка. В C# всички променливи, включително и елементите на масивите имат начална стойност по подразбиране (default initial value). Тази стойност е равна на 0 при числените типове или неин еквивалент при нечислени типове (например null за референтни типове и false за булевия тип).
Разбира се, начални стойности можем да задавам и изрично. Това може да стане по различни начини. Ето един от тях:
|
int[] myArray = { 1, 2, 3, 4, 5, 6 }; |
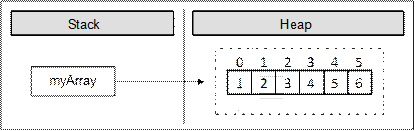
В този случай създаваме и инициализираме елементите на масива едновременно. Ето как изглежда масивът в паметта, след като стойностите му са инициализирани още в момента на деклариране:
При този синтаксис къдравите скоби заместват оператора new и между тях са изброени началните стойности на масива, разделени със запетаи. Техния брой определя дължината му.
Деклариране и инициализиране на масив – пример
Ето още един пример за деклариране и непосредствено инициализиране на масив:
|
string[] daysOfWeek = { "Monday", "Tuesday", "Wednesday","Thursday", "Friday", "Saturday", "Sunday" }; |
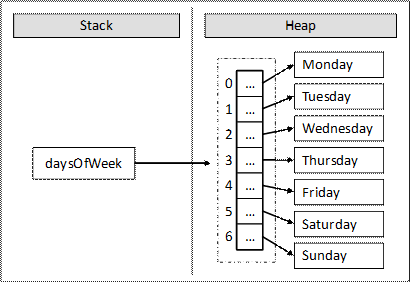
В случая масивът се заделя със 7 елемента от тип string. Типът string е референтен тип (обект) и неговите стойности се пазят в динамичната памет. В стека се заделя променливата daysOfWeek, която сочи към участък в динамичната памет, който съдържа елементите на масива. Всеки от тези 7 елемента е обект от тип символен низ (string), който сам по себе си сочи към друга област от динамичната памет, в която се пази стойността му.
Ето как е разположен масивът в паметта:
Граници на масив
Масивите по подразбиране са нулево-базирани, т.е. номерацията на елементите започва от 0. Първият елемент има индекс 0, вторият 1 и т.н. Ако един масив има N елемента, то последният елемент се намира на индекс N-1.
Достъп до елементите на масив
Достъпът до елементите на масивите е пряк и се осъществява по индекс. Всеки елемент може да се достъпи с името на масива и съответния му индекс (пореден номер), поставен в квадратни скоби. Можем да осъществим достъп до даден елемент както за четене така и за писане т.е. да го третираме като най-обикновена променлива.
Пример за достъп до елемент на масив:
|
myArray[index] = 100; |
В горния пример присвояваме стойност 100 на елемента, намиращ се на позиция index.
Ето един пример, в който заделяме масив от числа и след това променяме някои от елементите му:
|
int[] myArray = new int[6]; myArray[1] = 1; myArray[5] = 5; |
След промяната на елементите, масивът се представя в паметта по следния начин:
Както се вижда, всички елементи, с изключение на тези, на които изрично сме задали стойност, са инициализирани с 0 при заделянето на масива.
Масивите могат да се обхождат с помощта на някоя от конструкциите за цикъл, като най-често използван е класическият for цикъл:
|
int[] arr = new int[5]; for (int i = 0; i < arr.Length; i++) { arr[i] = i; } |
Излизане от границите на масив
При всеки достъп до елемент на масив .NET Framework прави автоматична проверка, дали индексът е валиден или е извън границите на масива. При опит за достъп до невалиден елемент се хвърля изключение от типSystem.IndexOutOfRangeException. Автоматичната проверка за излизане от границите на масива е изключително полезна за разработчиците и води до ранно откриване на грешки при работа с масиви. Естествено, тези проверки си имат и своята цена и тя е леко намаляване на производителността, която е нищожна в сравнение с избягването на грешки от тип "излизане от масив", "достъп до незаделена памет" и други.
Ето един пример, в който се опитваме да извлечем елемент, който се намира извън границите на масива:
|
IndexOutOfRangeExample.cs |
|
classIndexOutOfRangeExample { static void Main() { int[] myArray = { 1, 2, 3, 4, 5, 6 }; Console.WriteLine(myArray[6]); } } |
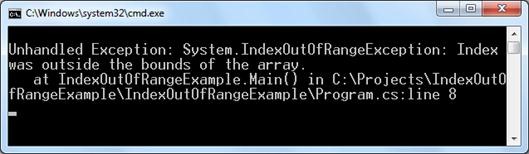
В горния пример създаваме масив, който съдържа 6 цели числа. Първият елемент се намира на индекс 0, а последният – на индекс 5. Опитваме се да изведем на конзолата елемент, който се намира на индекс 6, но понеже такъв не съществува, това води до възникване на изключение:
Обръщане на масив в обратен ред – пример
В следващия пример ще видим как може да променяме елементите на даден масив като ги достъпваме по индекс. Целта на задачата е да се подредят в обратен ред (отзад напред) елементите на даден масив. Ще обърнем елементите на масива, като използваме помощен масив, в който да запазим елементите на първия, но в обратен ред. Забележете, че дължината на масивите е еднаква и остава непроменена след първоначалното им заделяне:
|
ArrayReverseExample.cs |
|
classArrayReverseExample { static void Main() { int[] array = { 1, 2, 3, 4, 5 }; // Get array size int length = array.Length; // Declare and create the reversed array int[] reversed = new int[length];
// Initialize the reversed array for (int index = 0; index < length; index++) { reversed[length - index - 1] = array[index]; }
// Print the reversed array for (int index = 0; index < length; index++) { Console.Write(reversed[index]+ " "); } } } // Output: 5 4 3 2 1 |
Примерът работи по следния начин: първоначално създаваме едномерен масив от тип int и го инициализираме с цифрите от 1 до 5. След това запазваме дължината на масива в целочислената променлива length. Забележете, че се използва свойството Length, което връща броя на елементите на масива. В C# всеки масив знае своята дължина.
След това декларираме масив reversed със същия размер length, в който ще си пазим елементите на оригиналния масив, но в обратен ред.
За да извършим обръщането на елементите използваме цикъл for, като на всяка итерация увеличаваме водещата променлива index с единица и така си осигуряваме последователен достъп до всеки елемент на масива array. Критерият за край на цикъла ни подсигурява, че масивът ще бъде обходен от край до край.
Нека проследим последователно какво се случва при итериране върху масива array. При първата итерация на цикъла, index има стойност 0. С array[index] достъпваме първия елемент на масива array, а съответно с reversed[length - index - 1] достъпваме последния елемент на новия масив reversed и извършваме присвояване. Така на последния елемент на reversed присвоихме първия елемент на array. На всяка следваща итерация index се увеличава с единица, позицията в array се увеличава с единица, а в reversed се намаля с единица.
В резултат обърнахме масива в обратен ред и го отпечатахме. В примера показахме последователно обхождане на масив, което може да се извърши и с другите видове цикли (например while и foreach).
Четене на масив от конзолата
Нека разгледаме как можем да прочетем стойностите на масив от конзолата. Ще използваме for цикъл и средствата на .NET Framework за четене от конзолата.
Първоначално, прочитаме един ред от конзолата с помощта на Console.ReadLine(), след това преобразуваме прочетения ред към цяло число с помощта на int.Parse() и го присвояваме на n. Числото n ползваме по-нататък като размер на масива.
|
int n = int.Parse(Console.ReadLine()); int[] array = new int[n]; |
Отново използваме цикъл, за да обходим масива. На всяка итерация присвояваме на текущия елемент прочетеното от конзолата число. Цикълът ще се завърти n пъти т.е. ще обходи целия масив и така ще прочетем стойност за всеки един елемент от масива:
|
for (int i = 0; i < n; i++) { array[i] = int.Parse(Console.ReadLine()); } |
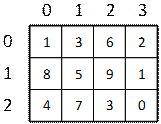
Проверка за симетрия на масив – пример
Един масив е симетричен, ако първият и последният му елемент са еднакви и същевременно вторият и предпоследният му елемент също са еднакви и т.н. На картинката са дадени няколко примера за симетрични масиви:
В следващия примерен код ще видим как можем да проверим дали даден масив е симетричен:
|
Console.Write("Enter a positive integer: "); int n = int.Parse(Console.ReadLine()); int[] array = new int[n];
Console.WriteLine("Enter the values of the array:");
for (int i = 0; i < n; i++) { array[i] = int.Parse(Console.ReadLine()); }
bool symmetric = true; for (int i = 0; i < array.Length / 2; i++) { if (array[i] != array[n - i - 1]) { symmetric = false; } }
Console.WriteLine("Is symmetric? {0}", symmetric); |
Тук отново създаваме масив и прочитаме елементите му от конзолата. За да проверим дали масивът е симетричен, трябва да го обходим само до средата. Тя е елементът с индекс array.Length / 2. При нечетна дължина на масива този индекс е средният елемент, а при нечетна – елементът вляво от средата (понеже средата е между два елемента).
За да определим дали даденият масив е симетричен ще ползваме булева променлива, като първоначално приемаме, че масивът е симетричен.
Обхождаме масива и сравняваме първия с последния елемент, втория с предпоследния и т.н. Ако за някоя итерация се окаже, че стойностите на сравняваните елементи не съвпадат, булевата променлива получава стойност false, т.е. масивът не е симетричен.
Накрая извеждаме на конзолата стойността на булевата променлива.
Отпечатване на масив на конзолата
Често се налага след като сме обработвали даден масив да изведем елементите му на конзолата, било то за тестови или други цели.
Отпечатването на елементите на масив става по подобен начин на инициализирането на елементите му, а именно като използваме цикъл, който обхожда масива. Няма строги правила за начина на извеждане на елементите, но често пъти се ползва подходящо форматиране.
Често срещана грешка е опит да се изведе на конзолата масив директно, по следния начин:
|
string[] array = { "one", "two", "three", "four" }; Console.WriteLine(array); |
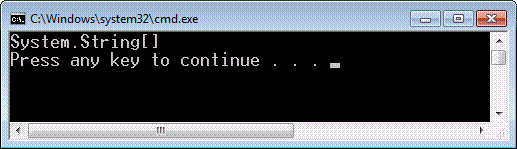
Този код за съжаление не отпечатва съдържанието на масива, а неговия тип. Ето как изглежда резултатът от изпълнението на горния пример:
За да изведем коректно елементите на масив на конзолата можем да използваме for цикъл:
|
string[] array = { "one", "two", "three", "four" };
for (int index = 0; index < array.Length; index++) { // Print each element on a separate line Console.WriteLine("Element[{0}] = {1}", index, array[index]); } |
Обхождаме масива с цикъл for, който извършва array.Length на брой итерации, и с помощта на метода Consolе.WriteLine() извеждаме поредния му елемент на конзолата чрез форматиращ стринг. Резултатът е следният:
|
Element[0] = one Element[1] = two Element[2] = three Element[3] = four |
Итерация по елементите на масив
Както разбрахме до момента, итерирането по елементите на масив е една от основните операции при обработката на масиви. Итерирайки последователно по даден масив можем да достъпим всеки елемент с помощта на индекс и да го обработваме по желан от нас начин. Това може да стане с всички видове конструкции за цикъл, които разгледахме в предната тема, но най-подходящ за това е стандартният for цикъл. Нека разгледаме как точно става обхождането на масиви.
Итерация с for цикъл
Добра практика е да използваме for цикъл при работа с масиви и изобщо при индексирани структури. Ето един пример, в който удвояваме стойността на всички елементи от даден масив с числа и го принтираме:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Output: "); for (int index = 0; index < array.Length; index++) { //Doubling the number array[index] = 2 * array[index]; //Print the number Console.Write(array[index] + " "); } // Output: 2 4 6 8 10 |
Чрез for цикъла можем да имаме постоянен поглед върху текущия индекс на масива и да достъпваме точно тези елементи, от които имаме нужда. Итерирането може да не се извършва последователно т.е. индексът, който for цикъла ползва може да прескача по елементите според нуждите на нашия алгоритъм. Например можем да обходим част от даден масив, а не всичките му елементи:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Output: "); for (int index = 0; index < array.Length; index += 2) { array[index] = array[index] * array[index]; Console.Write(array[index] + " "); } // Output: 1 9 25 |
В горния пример обхождаме всички елементи на масива, намиращи се на четни позиции и повдигаме на квадрат стойността във всеки от тях.
Понякога е полезно да обходим масив отзад напред. Можем да постигнем това по напълно аналогичен начин, с разликата, че for цикълът ще започва с начален индекс, равен на индекса на последния елемент на масива, и ще се намаля на всяка итерация докато достигне 0 (включително). Ето един такъв пример:
|
int[] array = new int[] { 1, 2, 3, 4, 5 };
Console.Write("Reversed: "); for (int index = array.Length - 1; index >= 0; index--) { Console.Write(array[index] + " "); } //Reversed: 5 4 3 2 1 |
В горния пример обхождаме масива отзад напред последователно и извеждаме всеки негов елемент на конзолата.
Итерация с цикъл foreach
Една често използвана конструкция за итерация по елементите на масив е така нареченият foreach. Конструкцията на foreach цикъла в C# е следната:
|
foreach (var item in collection) { // Process the value here } |
При тази конструкция var е типът на елементите, които обхождаме т.е. типа на масива, collection е масивът (или някаква друга колекция от елементи), а item е текущият елемент от масива на всяка една стъпка от обхождането.
Цикълът foreach притежава в голяма степен свойствата на for цикъла. Отличава се с това, че преминаването през елементите на масива (или на колекцията, която се обхожда), се извършва винаги от край до край. При него не е достъпен индексът на текущата позиция, а просто се обхождат всички елементи в ред, определен от самата колекция, която се обхожда. За масивите редът на обхождане е последователно от нулевия към последния елемент.
Този цикъл се използва, когато нямаме нужда да променяме елементите на масива, а само да ги четем и да обхождаме целия масив.
Итерация с цикъл foreach – пример
В следващия пример ще видим как да използваме конструкцията на foreach цикълa за обхождане на масиви:
|
string[] capitals = { "Sofia", "Washington", "London", "Paris" };
foreach (string capital in capitals) { Console.WriteLine(capital); } |
След като сме си декларирали масив от низове capitals, с foreach го обхождаме и извеждаме елементите му на конзолата. Текущият елемент на всяка една стъпка се пази в променливата capital. Ето какъв резултат се получава при изпълнението на примера:
|
Sofia Washington London Paris |
Многомерни масиви
До момента разгледахме работата с едномерните масиви, известни в математиката като "вектори". В практиката, обаче, често се ползват масиви с повече от едно измерения. Например стандартна шахматна дъска се представя лесно с двумерен масив с размер 8 на 8 (8 полета в хоризонтална посока и 8 полета във вертикална посока).
Какво е "многомерен масив"? Какво е "матрица"?
Всеки допустим в C# тип може да бъде използван за тип на елементите на масив. Масивите също може да се разглеждат като допустим тип. Така можем да имаме масив от масиви, който ще разгледаме по-нататък.
Едномерен масив от цели числа декларираме с int[], а двумерен масив с int[,]. Следния пример показва това:
|
int[,] twoDimentionalArray; |
Такива масиви ще наричаме двумерни, защото имат две измерения или още матрици (терминът идва от математиката). Масиви с повече от едно измерение ще наричаме многомерни.
Аналогично можем да декларираме и тримерни масиви като добавим още едно измерение:
|
int[,,] threeDimentionalArray; |
На теория няма ограничения за броя на размерностите на тип на масив, но в практиката масиви с повече от две размерности са рядко използвани и затова ще се спрем по-подробно на двумерните масиви.
Деклариране и заделяне на многомерен масив
Многомерните масиви се декларират по начин аналогичен на едномерните. Всяка тяхна размерност (освен първата) означаваме със запетая:
|
int[,] intMatrix; float[,] floatMatrix; string[,,] strCube; |
Горният пример показва как да създадем двумерни и тримерни масиви. Всяка размерност в допълнение на първата отговаря на една запетая в квадратните скоби [].
Памет за многомерни размери се заделя като се използва ключовата дума new и за всяка размерност в квадратни скоби се задава размерът, който е необходим:
|
int[,] intMatrix = new int[3, 4]; float[,] floatMatrix = new float[8, 2]; string[,,] stringCube = new string[5, 5, 5]; |
В горния пример intMatrix е двумерен масив с 3 елемента от тип int[] и всеки от тези 3 елемента има размерност 4. Така представени, двумерните масиви изглеждат трудни за осмисляне. Затова може да ги разглеждаме като двумерни матрици, които имат редове и колони за размерности:
Редовете и колоните на квадратните матрици се номерират с индекси от 0 до n-1. Ако един двумерен масив има размер m на n, той има точно m*n елемента.
Инициализация на двумерен масив
Инициализацията на многомерни масиви е аналогична на инициализацията на едномерните. Стойностите на елементите могат да се изброяват непосредствено след декларацията:
|
int[,] matrix = { {1, 2, 3, 4}, // row 0 values {5, 6, 7, 8}, // row 1 values }; // The matrix size is 2 x 4 (2 rows, 4 cols) |
В горния пример инициализираме двумерен масив с цели числа с 2 реда и 4 колони. Във външните фигурни скоби се поставят елементите от първата размерност, т.е. редовете на двумерната матрица. Всеки ред представлява едномерен масив, който се инициализира по познат за нас начин.
Достъп до елементите на многомерен масив
Матриците имат две размерности и съответно всеки техен елемент се достъпва с помощта на два индекса – един за редовете и един за колоните. Многомерните масиви имат различен индекс за всяка размерност.
|
Всяка размерност в многомерен масив започва от индекс нула. |
Нека разгледаме следния пример:
|
int[,] matrix = { {1, 2, 3, 4}, {5, 6, 7, 8}, }; |
Масивът matrix има 8 елемента, разположени в 2 реда и 4 колони. Всеки елемент може да се достъпи по следния начин:
|
matrix[0, 0] matrix[0, 1] matrix[0, 2] matrix[0, 3] matrix[1, 0] matrix[1, 1] matrix[1, 2] matrix[1, 3] |
В горния пример виждаме как да достъпим всеки елемент по индекс. Ако означим индекса по редове с row, а индекса по колони с col, тогава достъпа до елемент от двумерен масив има следния общ вид:
|
matrix[row, col] |
При многомерните масиви всеки елемент се идентифицира уникално с толкова на брой индекси, колкото е размерността на масива:
|
nDimensionalArray[index1, … , indexN] |
Дължина на многомерен масив
Всяка размерност на многомерен масив има собствена дължина, която е достъпна по време на изпълнение на програмата. Нека разгледаме следния пример за двумерен масив:
|
int[,] matrix = { {1, 2, 3, 4}, {5, 6, 7, 8}, }; |
Можем да извлечем броя на редовете на този двумерен масив чрез matrix.GetLength(0), а дължината на всеки от редовете (т.е. броя колони) с matrix.GetLength(1).
Отпечатване на матрица – пример
Чрез следващия пример ще демонстрираме как можем да отпечатваме двумерни масиви на конзолата:
|
// Declare and initialize a matrix of size 2 x 4 int[,] matrix = { {1, 2, 3, 4}, // row 0 values {5, 6, 7, 8}, // row 1 values };
for (int row = 0; row < matrix.GetLength(0); row++) { for (int col = 0; col < matrix.GetLength(1); col++) { Console.Write(matrix[row, col]); } Console.WriteLine(); } // Print the matrix on the console |
Първо декларираме и инициализираме масива, който искаме да обходим и да отпечатаме на конзолата. Масивът е двумерен и затова използваме един цикъл, който ще се движи по редовете и втори, вложен цикъл, който за всеки ред ще се движи по колоните на масива. За всяка итерация по подходящ начин извеждаме текущия елемент на масива като го достъпваме по неговите два индекса (ред и колона). В крайна сметка, ако изпълним горния програмен фрагмент, ще получим следния резултат:
|
1 2 3 4 5 6 7 8 |
Четене на матрица от конзолата – пример
Нека видим как можем да прочетем двумерен масив (матрица) от конзолата. Това става като първо въведем големините на двете размерности, а след това с два вложени цикъла въвеждаме всеки от елементите му:
|
Console.Write("Enter the number of the rows: "); int rows = int.Parse(Console.ReadLine());
Console.Write("Enter the number of the columns: "); int cols = int.Parse(Console.ReadLine());
int[,] matrix = new int[rows, cols];
Console.WriteLine("Enter the cells of the matrix:");
for (int row = 0; row < rows; row++) { for (int col = 0; col < cols; col++) { Console.Write("matrix[{0},{1}] = ",row,col); matrix[row, col] = int.Parse(Console.ReadLine()); } }
for (int row = 0; row < matrix.GetLength(0); row++) { for (int col = 0; col < matrix.GetLength(1); col++) { Console.Write(" " + matrix[row, col]); } Console.WriteLine(); } |
Ето как може да изглежда програмата в действие (в случая въвеждаме масив с размер 3 реда на 2 колони):
|
Enter the number of the rows: 3 Enter the number of the columns: 2 Enter the cells of the matrix: matrix[0,0] = 2 matrix[0,1] = 3 matrix[1,0] = 5 matrix[1,1] = 10 matrix[2,0] = 8 matrix[2,1] = 9 2 3 5 10 8 9 |
Максимална площадка в матрица – пример
В следващия пример ще решим една по-интересна задача: дадена е правоъгълна матрица с числа и трябва да намерим в нея максималната подматрица с размер 2 х 2 и да я отпечатаме на конзолата. Под максимална подматрица ще разбираме подматрица, която има максимална сума на елементите, които я съставят. Ето едно примерно решение на задачата:
|
MaxPlatform2x2.cs |
|
classMaxPlatform2x2 { static void Main() { //Declare and initialize the matrix int[,] matrix = { { 0, 2, 4, 0, 9, 5 }, { 7, 1, 3, 3, 2, 1 }, { 1, 3, 9, 8, 5, 6 }, { 4, 6, 7, 9, 1, 0 } };
// Find the maximal sum platform of size 2 x 2 int bestSum = int.MinValue; int bestRow = 0; int bestCol = 0;
for (int row = 0; row < matrix.GetLength(0) - 1; row++) { for (int col = 0; col < matrix.GetLength(1) - 1; col++) { int sum = matrix[row, col] + matrix[row, col + 1] + matrix[row + 1, col] + matrix[row + 1, col + 1]; if (sum > bestSum) { bestSum = sum; bestRow = row; bestCol = col; } } }
// Print the result Console.WriteLine("The best platform is:"); Console.WriteLine(" {0} {1}", matrix[bestRow, bestCol], matrix[bestRow, bestCol + 1]); Console.WriteLine(" {0} {1}", matrix[bestRow + 1, bestCol], matrix[bestRow + 1, bestCol + 1]); Console.WriteLine("The maximal sum is: {0}", bestSum); } } |
Ако изпълним програмата, ще се убедим, че работи коректно:
|
The best platform is: 9 8 7 9 The maximal sum is: 33 |
Нека сега обясним реализирания алгоритъм. В началото на програмата си създаваме двумерен масив, състоящ се от цели числа. Декларираме помощни променливи bestSum, bestRow, bestCol и инициализираме bestSum с минималната за типа intстойност (така че всяка друга да е по-голяма от нея).
В променливата bestSum ще пазим текущата максимална сума, а в bestRow и bestCol ще пазим най-добрата до момента подматрица, т.е. текущият ред и колона, които са начало на подматрицата с размери 2 х 2, имаща сума на елементите bestSum.
За да достъпим всички елементи на подматрица 2 х 2 са ни необходими индексите на първия й елемент. Като ги имаме лесно можем да достъпим другите 3 елемента по следния начин:
|
matrix[row, col] matrix[row, col+1] matrix[row+1, col] matrix[row+1, col+1] |
В горния пример row и col са индексите на отговарящи на първия елемент на матрица с размер 2 х 2, която е част от матрицата matrix.
След като вече разбрахме как да достъпим четирите елемента на матрица с размер 2 х 2, започващи от даден ред и колона, можем да разгледаме алгоритъма, по който ще намерим максималната такава матрица 2 x 2.
Трябва да обходим всеки елемент от главната матрица до предпоследния ред и предпоследната колона. Това правим с два вложени цикъла по променливите row и col. Забележете, че не обхождаме матрицата от край до край, защото при опит да достъпим индекси row + 1 или col + 1 ще излезем извън границите на масива ако сме на последния ред или колона и ще възникне изключение System.IndexOutOfRangeException.
Достъпваме съседните елементи на всеки текущ начален елемент на подматрица с размер 2 х 2 и ги сумираме. След това проверяваме дали текущата ни сума е по-голяма от текущата най-голяма сума. Ако е така текущата сума става текуща най-голяма сума и текущите индекси стават bestRow и bestCol. Така след пълното обхождане на главната матрица ще намерим максималната сума и индексите на началния елемент на подматрицата с размери 2 x 2, имаща тази най-голяма сума. Ако има няколко подматрици с еднаква максимална сума, ще намерим тази, която се намира на минимален ред и минимална колона в този ред.
В края на примера извеждаме на конзолата по подходящ начин търсената подматрица и нейната сума.
Масиви от масиви
В C# можем да използваме масив от масиви или така наречените назъбени (jagged) масиви.
Назъбените масиви представляват масиви от масиви или по-точно масиви, в които един ред на практика е също масив и може да има различна дължина от останалите в назъбения масив.
Деклариране и заделяне на масив от масиви
Единственото по-особено при назъбените масиви е, че нямаме само една двойка скоби, както при обикновените масиви, а имаме вече по една двойка скоби за всяко от измеренията. Заделянето става по същия начин:
|
int[][] jaggedArray; jaggedArray = new int[2][]; jaggedArray[0] = new int[5]; jaggedArray[1] = new int[3]; |
Ето как декларираме, заделяме и инициализираме един масив от масиви:
|
int[][] myJaggedArray = { new int[] {5, 7, 2}, new int[] {10, 20, 40}, new int[] {3, 25} }; |
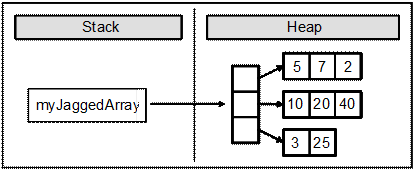
Разположение в паметта
На долната картинка може да се види вече дефинираният назъбен масив myJaggedArrayили по-точно неговото разположение в паметта. Както се вижда самият назъбен масив представлява съвкупност от референции, а не съдържа самите масиви. Не се знае каква е размерността на масивите и затова CLR пази само референциите (указателите) към тях. След като заделим памет за някой от масивите-елементи на назъбения, тогава се насочва указателят към новосъздадения блок в динамичната памет. Променливата myJaggedArray стои в стека за изпълнение на програмата и сочи към блок от динамичната памет, съдържащ поредица от три указателя към други блокове от паметта, всеки от които съдържа масив от цели числа – елементите на назъбения масив:
Инициализиране и достъп до елементите
Достъпът до елементите на масивите, които са част от назъбения, отново се извършва по индекса им. Ето пример за достъп до елемента с индекс 3 от масива, който се намира на индекс 0 в по-горе дефинирания назъбен масив jaggedArray:
|
myJaggedArray[0][3] = 45; |
Елементите на назъбения масив може да са както едномерни масиви, така и многомерни такива. Ето един пример за назъбен масив от двумерни масиви:
|
int[][,] jaggedOfMulti = new int[2][,]; jaggedOfMulti[0] = new int[,] { { 5, 15 }, { 125, 206 } }; jaggedOfMulti[1] = new int[,] { { 3, 4, 5 }, { 7, 8, 9 } }; |
Триъгълник на Паскал – пример
В следващия пример ще използваме назъбен масив, за да генерираме и визуализираме триъгълника на Паскал. Както знаем от математиката, първият ред на триъгълника на Паскал съдържа числото 1, а всяко число от всеки следващ ред се образува като се съберат двете числа от горния ред над него. Триъгълникът на Паскал изглежда по следния начин:
|
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 . . . |
За да получим триъгълника на Паскал до дадена височина, например 12, можем да заделим назъбен масив triangle[][], който съдържа 1 елемент на нулевия си ред, 2 – на първия, 3 – на втория и т.н. Първоначално инициализираме triangle[0][0] = 1, а всички останали клетки на масива получават по подразбиране стойност 0 при заделянето им. След това въртим цикъл по редовете, в който от стойностите на ред row получаваме стойностите на ред row+1. Това става с вложен цикъл по колоните на текущия ред, следвайки дефиницията за стойностите в триъгълника на Паскал: прибавяме стойността на текущата клетка от текущия ред (triangle[row][col]) към клетката под нея (triangle[row+1][col]) и клетката под нея вдясно (triangle[row+1][col+1]). При отпечатването се добавят подходящ брой интервали отляво (чрез метода PadRight() на класа String), за да изглежда резултатът по-подреден.
Следва примерна реализация на описания алгоритъм:
|
PascalTriangle.cs |
|
classPascalTriangle { static void Main() { const int HEIGHT = 12;
// Allocate the array in a triangle form long[][] triangle = new long[HEIGHT + 1][];
for (int row = 0; row < HEIGHT; row++) { triangle[row] = new long[row + 1]; }
// Calculate the Pascal's triangle triangle[0][0] = 1; for (int row = 0; row < HEIGHT - 1; row++) { for (int col = 0; col <= row; col++) { triangle[row + 1][col] += triangle[row][col]; triangle[row + 1][col + 1] += triangle[row][col]; } }
// Print the Pascal's triangle for (int row = 0; row < HEIGHT; row++) { Console.Write("".PadLeft((HEIGHT - row) * 2)); for (int col = 0; col <= row; col++) { Console.Write("{0,3} ", triangle[row][col]); } Console.WriteLine(); } } } |
Ако изпълним програмата, ще се убедим, че тя работи коректно и генерира триъгълника на Паскал със зададената височина:
|
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 1 11 55 165 330 462 462 330 165 55 11 1 |
Упражнения
1. Да се напише програма, която създава масив с 20 елемента от целочислен тип и инициализира всеки от елементите със стойност равна на индекса на елемента умножен по 5. Елементите на масива да се изведат на конзолата.
2. Да се напише програма, която чете два масива от конзолата и проверява дали са еднакви.
3. Да се напише програма, която сравнява два масива от тип char лексикографски (буква по буква) и проверява кой от двата е по-рано в лексикографската подредба.
4. Напишете програма, която намира максимална редица от последователни еднакви елементи в масив. Пример: {2, 1, 1, 2, 3, 3, 2, 2, 2, 1} à {2, 2, 2}.
5. Напишете програма, която намира максималната редица от последователни нарастващи елементи в масив. Пример: {3, 2, 3, 4, 2, 2, 4} à {2, 3, 4}.
6. Напишете програма, която намира максималната подредица от нарастващи елементи в масив arr[n]. Елементите може и да не са последователни. Пример: {9, 6, 2, 7, 4, 7, 6, 5, 8, 4} à {2, 4, 6, 8}.
7. Да се напише програма, която чете от конзолата две цели числа N и K (K<N), и масив от N елемента. Да се намерят тези K поредни елемента, които имат максимална сума.
8. Сортиране на масив означава да подредим елементите му в нарастващ (намаляващ) ред. Напишете програма, която сортира масив. Да се използва алгоритъма "Selection sort".
9. Напишете програма, която намира последователност от числа, чиито сума е максимална. Пример: {2, 3, -6, -1, 2, -1, 6, 4, -8, 8} à11
10. Напишете програма, която намира най-често срещания елемент в масив. Пример: {4, 1, 1, 4, 2, 3, 4, 4, 1, 2, 4, 9, 3} à 4 (среща се 5 пъти).
11. Да се напише програма, която намира последователност от числа в масив, които имат сума равна на число, въведено от конзолата (ако има такава). Пример: {4, 3, 1, 4, 2, 5, 8}, S=11 à {4, 2, 5}.
12. Напишете програма, която създава следните квадратни матрици и ги извежда на конзолата във форматиран вид. Размерът на матриците се въвежда от конзолата. Пример за (4,4):
13. Да се напише програма, която създава правоъгълна матрица с размер n на m. Размерността и елементите на матрицата да се четат от конзолата. Да се намери подматрицата с размер (3,3), която има максимална сума.
14. Да се напише програма, която намира най-дългата последователност от еднакви stringелементи в матрица. Последователност в матрица дефинираме като елементите са на съседни и са на същия ред,колона или диагонал.
15. Да се напише програма, която създава масив с всички букви от латинската азбука. Да се даде възможност на потребител да въвежда дума от конзолата и в резултат да се извеждат индексите на буквите от думата.
16. Да се реализира двоично търсене (binary search) в сортиран целочислен масив.
17. Напишете програма, която сортира целочислен масив по алгоритъма "merge sort".
18. Напишете програма, която сортира целочислен масив по алгоритъма "quick sort".
19. Напишете програма, която намира всички прости числа в диапазона [1…10 000 000].
20. Напишете програма, която по дадени N числа и число S, проверявадали може да се получи сума равна на S с използване на подмасив от N-те числа (не непременно последователни).
Пример: {2, 1, 2, 4, 3, 5, 2, 6}, S = 14 à yes (1 + 2 + 5 + 6 = 14)
21. Напишете програма, която по дадени N, K и S, намира К на брой елементи измежду N-те числа, чиито сума е точно S или показва, че това е невъзможно.
22. Напишете програма, която прочита от конзолата масив от цели числа и премахва минимален на брой числа, така че останали числа да са сортирани в нарастващ ред. Отпечатайте резултата.
Пример: {6, 1, 4, 3, 0, 3, 6, 4, 5} à {1, 3, 3, 4, 5}
23. Напишете програма, която прочита цяло число N от конзолата и отпечатва всички пермутации на числата [1…N].
Пример: N = 3 à {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}
24. Напишете програма, която прочита цели числа N и K от конзолата и отпечатва всички вариации от К елемента на числата [1…N].
Пример: N = 3, K = 2 à {1, 1}, {1, 2}, {1, 3}, {2, 1}, {2, 2}, {2, 3}, {3, 1}, {3, 2}, {3, 3}
25. Напишете програма, която прочита цяло число N отконзолата и отпечатва всички комбинации от К елемента на числата [1…N].
Пример: N = 5, K =2 à {1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 1}, {2, 3}, {2, 4}, {2, 5}, {3, 1}, {3, 4}, {3, 5}, {4, 5}
26. Напишете програма, която обхожда матрица (NxN) по следния начин:
Пример за N=4:
|
16 |
15 |
13 |
10 |
||||
|
14 |
12 |
9 |
6 |
||||
|
11 |
8 |
5 |
3 |
||||
|
7 |
4 |
2 |
1 |
||||
|
7 |
11 |
14 |
16 |
|
|||
|
4 |
8 |
12 |
15 |
|
|||
|
2 |
5 |
9 |
13 |
|
|||
|
1 |
3 |
6 |
10 |
|
|||
27. *Напишете програма, която по подадена матрица намира най-голямата област от еднакви числа. Под област разбираме съвкупност от съседни (по ред и колона) елементи. Ето един пример, в който имаме област, съставена от 13 на брой еднакви елементи със стойност 3:
Решения и упътвания
1. Използвайте масив int[] и for цикъл.
2. Два масива са еднакви, когато имат еднаква дължина и стойностите на елементите в тях съответно съвпадат. Второто условие можете да проверите с for цикъл.
3. При лексикографската наредба символите се сравняват един по един като се започва от най-левия. При несъвпадащи символи по-рано е масивът, чийто текущ символ е по-рано в азбуката. При съвпадение се продължава със следващия символ вдясно. Ако се стигне до края на единия масив, по-краткият е лексикографски по-рано. Ако всички съответни символи от двата масива съвпаднат, то масивите са еднакви и никой о тях не е по-рано в лексикографската наредба.
4. Сканирайте масива отляво надясно. Всеки път, когато текущото число е различно от предходното, от него започва нова подредица, а всеки път, когато текущото число съвпада с предходното, то е продължение на текущата подредица. Следователно, ако пазите в две променливи start и len съответно индекса на началото на текущата подредица от еднакви елементи (в началото той е 0) и дължината на текущата подредица (в началото той е 1), можете да намерите всички подредици от еднакви елементи и техните дължини. От тях лесно може да се избере най-дългата и да се запомня в две допълнителни променливи – bestStart и bestLen.
5. Тази задача е много подобна на предходната, но при нея даден елемент се счита за продължение на текущата редица тогава и само тогава, когато е по-голям от предхождащия го елемент.
6. Задачата може да се реши с два вложени цикъла и допълнителен масив len[0..n-1]. Нека в стойността len[i] пазим дължината на най-дългата нарастваща подредица, която започва някъде в масива (не е важно къде) и завършва с елемента arr[i]. Тогава len[0]=1, a len[x] е максималната сума max(1+len[prev]), където prev<x и arr[prev]<arr[x]. Следвайки дефиницията len[0..n-1] може да се пресметне с два вложени цикъла по следния начин: първият цикъл обхожда масива последователно отляво надясно с водеща променлива x. Вторият цикъл (който е вложен в първия) обхожда масива от началото до позиция x-1 и търси елемент prev с максимална стойност на len[prev], за който arr[prev]<arr[x]. След приключване на търсенето len[x] се инициализира с 1 + най-голямата намерена стойност на len[prev]или с 1, ако такава не е намерена.
Описаният алгоритъм намира дължините на всички максимални нарастващи подредици, завършващи във всеки негов елемент. Най-голямата от тези стойности е дължината на най-дългата нарастваща подредица. Ако трябва да намерим самите елементи съставящи тази максимална нарастваща подредица, можем да започнем от елемента, в който тя завършва (нека той е на индекс x), да го отпечатаме и да търсим предходния елемент (prev). За него е в сила, че prev<x и len[x]=1+len[prev]. Така намирайки и отпечатвайки предходния елемент докато има такъв, можем да намерим елементите съставящи най-дългата нарастваща подредица в обратен ред (от последния към първия).
7. Можете да проверите коя от поредица от K числа има най-голяма сума като проверите сумите на всички такива поредици. Първата такава поредица започва от индекс 0 и завършва в индекс K-1 и нека тя има сума S. Тогава втората редица от K елемента започва от индекс 1 и завършва в индекс K, като нейната сума може да се получи като от S се извади нулевия елемент и се добави K-ти елемент. По същия начин може да се продължи до достигане на края на редицата.
8. Потърсете в Интернет информация за алгоритъма "Selection sort" и неговите реализации. Накратко идеята е да се намери най-малкият елемент, после да се сложи на първа позиция, след това да се намери втория най-малък и да се сложи на втора позиция и т.н., докато целият масив се подреди в нарастващ ред.
9. Тази задача има два начина, по които може да се реши. Един от тях е с пълно изчерпване, т.е. с два цикъла проверяваме всяка възможна сума. Втория е масива да се обходи само с 1 цикъл като на всяко завъртане на цикъла проверяваме дали текущата сума е по-голяма от вече намерената максимална сума. Задачата може да се реши и с техниката "Динамично оптимиране". Потърсете повече за нея в Интернет.
10.Тази задача може да се решите по много начини. Един от тях е следният: взимате първото число и проверявате колко пъти се повтаря в масива, като пазите този брой в променлива. След всяко прочитане на еднакво число го заменяте с int.MinValue. След това взимате следващото и отново правите същото действие. Неговия брой срещания сравнявате с числото, което сте запазили в променливата и ако то е по-голямо, го присвоявате на променливата. Както се досещате, ако намерите число равно на int.MinValue преминавате към следващото.
Друг начин да решим задачата е да сортираме числата в нарастващ ред и тогава еднаквите числа ще бъдат разположени като съседни. Така задачата се свежда до намиране на най-дългата редица от съседни числа.
11.Задачата може да се реши с два вложени цикъла. Първият задава началната позиция за втория – от първия до последния елемент. Вторият цикъл започва от позицията, зададена от първия цикъл и сумира последователно числата надясно едно по едно, докато сумата не надвиши S. Ако сумата е равна на S, се запомня числото от първия цикъл (то е началото на поредицата) и числото от втория цикъл (то е краят на поредицата).
Ако всички числа са положителни, съществува и много по-бърз алгоритъм. Сумирате числата отляво надясно като започвате от нулевото. В момента, в който текущата сума надвиши S, премахвате най-лявото число от редицата и го изваждате от текущата сума. Ако тя пак е по-голяма от търсената, премахвате и следващото число отляво и т.н. докато текущата сума не стане по-малка от S. След това продължавате с поредното число отдясно. Ако намерите търсената сума, я отпечатвате заедно с редицата, която я образува. Така само с едно сканиране на елементите на масива и добавяне на числа от дясната страна към текущата редица и премахване на числа от лявата й страна (при нужда), решавате задачата.
12.Помислете за подходящи начини за итерация върху масивите с два вложени цикъла.
За d) може да приложите следната стратегия: започвате от позиция (0,0) и се движите надолу N пъти. След това се движите надясно N-1 пъти, след това нагоре N-1 пъти, след това наляво N-2 пъти, след това надолу N-2 пъти и т.н. При всяко преместване слагате в клетката, която напускате поредното число 1, 2, 3, ..., N.
13.Модифицирайте примера за максимална площадка с размер 2 x 2.
14.Задача може да се реши, като се провери за всеки елемент дали като тръгнем по диагонал, надолу или надясно, ще получим поредица. Ако получим поредица проверяваме дали тази поредица е по дълга от предходната най-дълга.
15.Задачата може да решите с масив и два вложени for цикъла (по буквите на думата и по масива за всяка буква). Задачата има и хитро решение без масив: индексът на дадена главна буква ch от латинската азбука може да се сметне чрез израза: (int) ch – (int) 'A'.
16.Потърсете в Интернет информация за алгоритъма "binary search". Какво трябва да е изпълнено, за да използваме този алгоритъм?
17.Потърсете в Интернет информация за алгоритъма "merge sort" и негови реализации.
18.Потърсете в Интернет информация за алгоритъма "quick sort" и негови реализации.
19.Потърсете в Интернет информация за "Sieve of Erathostenes" (Решетото на Ератостен, учено в часовете по математика).
20.Образувайте всички възможни суми по следния алгоритъм: взимате първото число и го маркирате като "възможна сума". След това взимате следващото подред число и за всяка вече получена "възможна сума" маркирате като възможна сумата на всяка от тях с поредното число. В момента, в който получите числото S, спирате с образуването на сумите. Можете да си пазите "възможните суми" или в булев масив където всеки индекс е някоя от сумите, или с по-сложна структура от данни (като Set например).
21.Подобна на задача 20 с тази разлика, че ако сумата е равна на S, но броя елементи е различен от К, продължаваме да търсим. Помислете как да пазите броя числа, с които сте получили определена сума.
22.Задачата може да се реши като се направи допълнителен масив със дължина броя на елементите. В този масив ще пазим текущата най-дълга редица с край елемента на този индекс.
23.Задачата може да се реши с рекурсия, прочетете глава "Рекурсия". Напишете подходяща рекурсия и всеки път променяме позицията на всеки елемент.
24.Подобна на 23 задача.
25.Подобна на 24 задача с тази разлика, че всички елементи в получената комбинация трябва да са във възходящ ред.
26.Помислете за подходящи начини за итерация върху масивите с два вложени цикъла. Разпишете обхождането на лист и помислете как да го реализирате с цикли и изчисления на индексите.
27.Тази задача е доста по-трудна от останалите. Може да използвате алгоритми за обхождане на граф, известни с названията "DFS" (Depth-first-search) или "BFS" (Breadth-first-search). Потърсете информация и примери за тях в Интернет или по-нататък в книгата.
Демонстрации (сорс код)
Изтеглете демонстрационните примери към настоящата глава от книгата: Масиви-Демонстрации.zip.
Дискусионен форум
Коментирайте книгата и задачите в нея във: форума на софтуерната академия.
7 отговора до “Глава 7. Масиви”
Коментирай
Трябва да сте влезнали, за да коментирате.

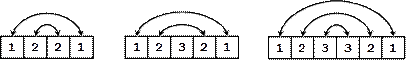
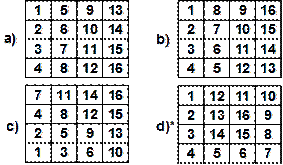

pomo6t za 6 zada4a ne namiram reshenie
Питай във форума: https://softuni.bg/forum/. Гарантирано ще получиш адекватен отговор.
reshih otdavna i bez foruma no nqkoi uputvaniq sa dosta oburkani..ina4e sa interesni zada4ite 🙂
Excelente la muestra del Ploitearna, mi curso el kinder B lo disfrutó mucho, y les hizo mucho sentido, ya que en nuestras clases lo habÃamos estudiado, los niños se acordaban les sirvió como refuerzo.
ee pi4uoue q kajete na 12-ta zadacha reshenieto pls she 4erpa we she vi kanim na vilata we
pi4uoue da dobavia she trebe i purva(1va) zadacha da q reshime she vikmen i kurvi vav vilata shte se cherpim stabilno she srutimeee konstrukciata bradddd
Здравейте!Търся,човек който да ми напише две задачи с масиви на езика C стандартен.