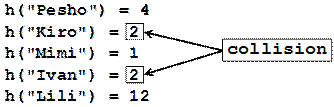Глава 18. Речници, хеш-таблици и множества
В тази тема...
В настоящата тема ще разгледаме някои по-сложни структури от данни като речници и множества, и техните реализации с хеш-таблици и балансирани дървета. Ще обясним в детайли какво представляват хеширането и хеш-таблиците и защо са токова важни в програмирането. Ще дискутираме понятието "колизия, как се получават колизиите при реализация на хеш-таблици и ще предложим различни подходи за разрешаването им. Ще разгледаме абстрактната структура данни "множество" и ще обясним как може да се реализира чрез речник и чрез балансирано дърво. Ще дадем примери, които илюстрират приложението на описаните структури от данни в практиката.
Съдържание
- Видео
- Презентация
- Мисловни карти
- В тази тема...
- Структура от данни "речник"
- Хеш-таблици
- Структура от данни "множество"
- Упражнения
- Решения и упътвания
- Демонстрации (сорс код)
- Дискусионен форум
Видео
Презентация
Мисловни карти
Структура от данни "речник"
В предните няколко теми се запознахме с някои класически и много важни структури от данни – масиви, списъци, дървета и графи. В тази - ще се запознаем с така наречените "речници" (dictionaries), които са изключително полезни и широко използвани в програмирането.
Речниците са известни още като асоциативни масиви (associative arrays) или карти (maps). Тук ще използваме терминът "речник". Всяко едно от различните имена подчертава една и съща характеристика на тази структура от данни, а именно, че в тях всеки елемент представлява съответствие между ключ и стойност – наредена двойка. Аналогията идва от факта, че в един речник, например тълковния речник, за всяка дума (ключ) имаме обяснение (стойност). Подобни са тълкованията и на другите имена.
|
При речниците заедно с данните, които държим, пазим и ключ, по който ги намираме. Елементите на речниците са двойки (ключ, стойност), като ключът се използва при търсене. |
Структура от данни "речник" – пример
Ще илюстрираме какво точно представлява структура от данни речник с един конкретен пример от ежедневието.
Когато отидете на театър, опера или концерт често преди да влезете в залата или стадиона има гардероб, в който може да оставите дрехите си. Там давате дрехата си на служителката от гардероба, тя я оставя на определено място и ви дава номерче. След като свърши представлението, на излизане давате вашето номерче, и чрез него служителката намира точно вашата дреха и ви я връща.
Чрез този пример виждаме, че идеята да разполагаме с ключ (номерче, което ви дава служителката) за данните (вашата дреха) и да ги достъпваме чрез него, не е толкова абстрактна. В действителност това е подход, който се среща на много места, както в програмирането така и в много сфери на реалния живот.
При структурата речник ключът може да не е просто номерче, а всякакъв друг обект. В случая, когато имаме ключ (номер), можем да реализираме такава структура като обикновен масив. Тогава множеството от ключове е предварително ясно – числата от 0 до n, където n е размерът на масива (естествено при разумно ограничение на n). Целта на речниците е да ни освободи, до колкото е възможно, от ограниченията за множеството на ключовете.
При речниците обикновено множеството от ключове е произволно множество от стойности, примерно реални числа или символни низове. Единственото задължително изискване е да можем да различим един ключ от друг. След малко ще се спрем по-конкретно на някои допълнителни изисквания към ключовете, необходими за различните реализации.
Речниците съпоставят на даден ключ дадена стойност. На един ключ може да се съпостави точно една стойност. Съвкупността от всички двойки (ключ, стойност) съставя речника.
Ето и първия пример за ползване на речник в .NET:
|
IDictionary<string, double> studentMarks =
studentMarks["Pesho"] = 3.00; Console.WriteLine("Pesho's mark: {0:0.00}", studentMarks["Pesho"]); |
По-нататък в главата ще разберем какъв ще бъде резултата от изпълнението на този пример.
Абстрактна структура данни "речник" (асоциативен масив, карта)
В програмирането абстрактната структура данни "речник" представлява съвкупност от наредени двойки (ключ, стойност), заедно с дефинирани операции за достъп до стойностите по ключ. Алтернативно тази структура може да бъде наречена още "карта" (map) или "асоциативен масив" (associative array).
Задължителни операции, които тази структура дефинира, са следните:
- void Add(K key, V value) – добавя в речника зададената наредена двойка. При повечето имплементации на класа в .NET, при добавяне на ключ, който вече съществува в речника, се хвърля изключение.
- V Get(K key) – връща стойността по даден ключ. Ако в речника няма двойка с такъв ключ, метода връща null, или хвърля изключение, според конкретната имплементация на речника
- bool Remove(key) – премахва стойността за този ключ от речника. Освен това връща дали е премахнат елемент от речника.
Ето и някои операции, които различните реализации на речници често предлагат:
- bool Contains(key) – връща true, ако в речникът има двойка с дадения ключ.
- int Count – връща броя елементи в речника.
Други операции, които обикновено се предлагат, са извличане на всички ключове, стойности или наредени двойки ключ-стойност, в друга структура (масив, списък). Така те лесно могат да бъдат обходени чрез цикъл.
|
За улеснение на .NET разработчиците, в интерфейса IDictionary<K, V> е добавено индексно свойство V this[K] { get; set; }, което обикновено се имплементира, чрез извикване на методите съответно V Get(K), Add(K, V). Трябва да имаме предвид, че метода за достъп (accessor) get на свойството V this[K] на класът Dictionary<K, V> в .NET хвърля изключение, ако даденият ключ K не присъства в речника. За да вземем стойността за даден ключ без да се опасяваме от изключения, можем да използваме метода - bool TryGetValue(K key, out V value) |
Интерфейсът IDictionary<K, V>
В .NET има дефиниран стандартен интерфейс IDictionary<K, V> където K дефинира типа на ключа (key), а V типа на стойността (value). Той дефинира всички основни операции, които речниците трябва да реализират. IDictionary<K, V> съответства на абстрактната структура от данни "речник" и дефинира операциите, изброени по-горе, но без да предоставя конкретна реализация за всяка от тях. Този интерфейс е дефиниран в асембли mscorelib, namespace System.Collections.Generic.
В .NET интерфейсите представляват спецификации за методите на даден клас. Те дефинират методи без имплементация, които след това трябва да бъдат имплементирани от класовете, обявили, че поддържа дадения интерфейс. Как работят интерфейсите и наследяването ще разгледаме подробно в главата "Принципи на обектно-ориентираното програмиране". За момента е достатъчно да знаете, че интерфейсите задават какви методи и свойства трябва да имат всички класове, които го имплементират.
В настоящата тема ще разгледаме двата най-разпространени начина за реализация на речници – балансирано дърво и хеш-таблица. Изключително важно е да се знае, по какво се различават те един от друг и какви са основните принципи, свързани с тях. В противен случай рискувате да ги използвате неправилно и неефективно.
В .NET има две основни имплементации на интерфейса IDictionary<K, V>: Dictionary<K, V> и SortedDictionary<K, V>. SortedDictionary представлява имплементация с балансирано (червено-черно) дърво, а Dictionary – имплементация с хеш-таблица.
|
Освен IDictionary<K, V> в .NET има още един интерфейс - IDictionary, както и класове които го имплементират: Hashtable, ListDictionary, HybridDictionаry. Те са наследство от първите версии на .NET. Тези класове трябва да се ползват само при специфична нужда. За предпочитане е употребата на Dictionary<K, V> или SortedDictionary<K, V>. |
В тази и следващата тема ще разгледаме в кои случаи се използват различните имплементации на речници в .NET.
Реализация на речник с червено-черно дърво
Тъй като имплементацията на речник чрез балансирано дърво е сложна и обширна задача, няма да я разглеждаме във вид на сорс код. Вместо това ще разгледаме класа SortedDictionary<K, V>, който идва наготово заедно със стандартните библиотеки на .NET. Силно препоръчваме на по-любознателните читатели да разгледат изходния код на SortedDictionary, използвайки някой от инструментите JustDecompiler или ILSpy, споменати в глава 1.
Както обяснихме в предходната глава, червено-черното дърво е подредено двоично балансирано дърво за претърсване. Ето защо едно от важните изисквания, които са наложени върху множеството от ключове при използването на SortedDictionary<K, V>, е те да имат наредба. Това означава, че ако имаме два ключа, то или единият е по-голям от другия, или те са равни.
Използването на двоично дърво ни носи едно силно предимство: ключовете в речника се пазят сортирани. Благодарение на това свойство, ако данните ни трябват подредени по ключ, няма нужда да ги сортираме допълнително. Всъщност това свойство е единственото предимство на тази реализация пред реализацията с хеш-таблица. Трябва да се подчертае обаче, че пазенето на ключовете сортирани идва със своята цена. Търсенето на елементите с балансирани дървета е по-бавна (сложност О(log n)) от работата с хеш-таблици O(1). По тази причина, ако няма специални изисквания за наредба на ключовете, за предпочитане е да се използва Dictionary<K, V>. Понятието сложност е обяснено в следващата тема.
|
Използвайте реализация на речник чрез балансирано дърво само когато се нуждаете от свойството наредените двойки винаги да са сортирани по ключ. Имайте предвид обаче, че балансираното дърво гарантира сложност на търсене, добавяне и изтриване от порядъка на log(n), докато сложността на търсене в хеш-таблицата може да достигне до линейна. |
Класът SortedDictionary<K, V>
Класът SortedDictionary<K, V> представлява имплементация на речник чрез червено-черно дърво. Този клас имплементира всички стандартни операции, дефинирани в интерфейса IDictionary<K, V>.
Използване на класа SortedDictionary – пример
Сега ще решим един практически проблем, където използването на класа SortedDictionary е уместно. Нека имаме някакъв текст. Нашата задача ще бъде да намерим всички различни думи в текста, както и колко пъти се среща всяка от тях. Като допълнително условие ще искаме да изведем намерените думи по азбучен ред.
При тази задача използването на речник се оказва особено подходящо. За ключове ще изберем думите от текста, а стойностите срещу всеки ключ в речника, ще бъдат броят срещания на съответната дума.
Алгоритъмът за броене на думите се състои в следното: четем текста дума по дума. За всяка дума проверяваме дали вече присъства в речника. Ако отговорът е не, добавяме нов елемент в речника с ключ думата и стойност 1 (броим първото срещане). Ако отговорът е да - увеличаваме старата стойност с единица за да преброим новото срещане на думата.
Използването на речник реализиран чрез балансирано дърво, ни дава свойството, когато обхождаме елементите му те да бъдат сортирани по ключ. По този начин реализираме допълнително наложеното условие думите да са сортирани по азбучен ред. Следва реализация на описания алгоритъм:
|
TreeMapExample.cs |
|
using System; using System.Collections.Generic; class TreeMapDemo { private static readonly string TEXT = "She uchish li she bachkash li? Be kvo she bachkash " + "be? Tui vashto uchene li e? Ia po-hubavo opitai da " + "BACHKASH da se uchish malko! Uchish ne uchish trqbva " + "da bachkash!";
static void Main() { IDictionary<String, int> wordOccurrenceMap = GetWordOccurrenceMap(TEXT); PrintWordOccurrenceCount(wordOccurrenceMap); }
private static IDictionary<string, int> GetWordOccurrenceMap( string text) {
string[] tokens = text.Split(' ', '.', ',', '-', '?', '!');
IDictionary<string, int> words = new SortedDictionary<string, int>();
foreach (string word in tokens) { if (string.IsNullOrEmpty(word.Trim())) { continue; }
int count; if (!words.TryGetValue(word, out count)) { count = 0; } words[word] = count + 1; } return words; }
private static void PrintWordOccurrenceCount( IDictionary<string, int> wordOccuranceMap) { foreach (KeyValuePair<string, int> wordEntry in wordOccuranceMap) { Console.WriteLine( "Word '{0}' occurs {1} time(s) in the text", wordEntry.Key, wordEntry.Value); }
Console.ReadKey(); } } |
Изходът от примерната програма е следният:
|
Word 'bachkash' occurs 3 time(s) in the text Word 'BACHKASH' occurs 1 time(s) in the text Word 'be' occurs 1 time(s) in the text Word 'Be' occurs 1 time(s) in the text … Word 'Tui' occurs 1 time(s) in the text Word 'uchene' occurs 1 time(s) in the text Word 'uchish' occurs 3 time(s) in the text Word 'Uchish' occurs 1 time(s) in the text Word 'vashto' occurs 1 time(s) in the text |
В този пример за пръв път демонстрираме обхождане на всички елементи на речник – методът PrintWordOccurrenceCount(IDictionary<string, int>). За целта използваме конструкцията за цикъл foreach. При обхождане на речници, трябва да обърнем внимание, че за разлика от списъците и масивите, елементите на тази структура от данни са наредени двойки (ключ и стойност), а не просто "единични" обекти. Както вече знаем обхождането на елементите на списък с foreach се свежда до извикване на методи на IEnumerable, който задължително се имплементира от класа на енумерирания обект. Тъй като IDictionary<K, V> имплементира интерфейса IEnumerable<KeyValuePair<K, V>>, това означава, че foreach итерира върху списък с обекти от тип KeyValuePair<K, V>.
Интерфейсът IComparable<K>
При използване на SortedDictionary<K, V> има задължително изискване ключовете да са от тип, чиито стойности могат да се сравняват по големина. В нашия пример ползваме за ключ обекти от тип string.
Класът string имплементира интерфейса IComparable, като сравнението е стандартно (лексикографски). Какво означава това? Тъй като по подразбиране низовете в .NET са case sensitive (т.е. има разлика между главна и малка буква), то думи като "Count" и "count" се смятат за различни, а думите, които започват с малка буква, са преди тези с голяма. Това е следствие от естествената наредба на низовете дефинирана в класа string. Тази дефиниция идва от имплементацията на метода CompareTo(object), чрез който класът string имплементира интерфейса IComparable.
Интерфейсът IComparer<T>
Какво можем да направим, когато естествената наредба не ни удовлетворява? Например, ако искаме при сравнението на думите да не се прави разлика между малки и главни букви.
Един вариант е след като прочетем дадена дума да я преобразуваме към малки или главни букви. Този подход ще работи за символни низове, но понякога ситуацията е по-сложна. Затова сега ще покажем друго решение, което работи за всеки произволен клас, който няма естествена наредба (не имплементира IComparable) или има естествена наредба, но ние искаме да я променим.
За сравнение на обекти по изрично дефинирана наредба в SortedDictionary<K, V> в .NET се използва интерфейс IComparer<T>. Той дефинира функция за сравнение int Compare(T x, T y), която задава алтернативна на естествената наредба. Нека разгледаме в детайли този интерфейс.
Когато създаваме обект от класа SortedDictionary<K, V> можем да подадем на конструктора му референция към IComparer<K> и той да използва него при сравнение на ключовете (които са елементи от тип K).
Ето една реализация на интерфейса IComparer<K>, която променя поведението при сравнение на низове, така че да не се различават по големи и малки букви
|
class CaseInsensitiveComparer : IComparer<string> { public int Compare(string s1, string s2) { return string.Compare(s1, s2, true); } } |
Нека използваме този IComparer<Е> при създаването на речника:
|
IDictionary<string, int> words = new CaseInsensitiveComparer()); |
След тази промяна резултатът от изпълнението на програмата ще бъде:
|
Word 'bachkash' occurs 4 time(s) in the text Word 'Be' occurs 2 time(s) in the text Word 'da' occurs 3 time(s) in the text ... Word 'Tui' occurs 1 time(s) in the text Word 'uchene' occurs 1 time(s) in the text Word 'uchish' occurs 4 time(s) in the text Word 'vashto' occurs 1 time(s) in the text |
Виждаме, че за ключ остава вариантът на думата, който е срещнат за първи път в текста. Това е така, тъй като при извикване на метода words[word] = count + 1 се подменя само стойността, но не и ключът.
Използвайки IComparer<Е> ние на практика сменихме дефиницията за подредба на ключове в рамките на нашия речник. Ако за ключ използвахме клас, дефиниран от нас, например Student, който имплементира IComparable<Е>, бихме могли да постигнем същия ефект чрез подмяна на реализацията на метода му CompareTo(Student). Има обаче едно изискване, което трябва винаги да се стремим да спазваме, когато имплементираме IComparable<K>. То гласи следното:
|
Винаги, когато два обекта са еднакви (Equals(object) връща true), CompareTo(Е) трябва да връща 0. |
Удовлетворяването на това условие ще ни позволи да ползваме обектите от даден клас за ключове, както в реализация с балансирано дърво (SortedDictionary, конструиран без Comparer), така и в реализация с хеш-таблица (Dictionary).
Хеш-таблици
Нека сега се запознаем със структурата от данни хеш-таблица, която реализира по един изключително ефективен начин абстрактната структура данни речник. Ще обясним в детайли как работят хеш-таблиците и защо са толкова ефективни.
Реализация на речник с хеш-таблица
Реализацията с хеш-таблица има важното предимство, че времето за достъп до стойност от речника, при правилно използване, теоретично не зависи от броя на елементите в него.
За сравнение да вземем списък с елементи, които са подредени в случаен ред. Искаме да проверим дали даден елемент се намира в него. В най-лошия случай, трябва да проверим всеки един елемент от него, за да дадем категоричен отговор на въпроса "съдържа ли списъкът елемента или не". Очевидно е, че броят на тези сравнения зависи (линейно) от броят на елементите в списъка.
При хеш-таблиците, ако разполагаме с ключ, броят сравнения, които трябва да извършим, за да установим има ли стойност с такъв ключ, е константен и не зависи от броя на елементите в нея. Как точно се постига такава ефективност ще разгледаме в детайли по-долу.
Когато реализациите на някои структури от данни ни дават време за достъп до елементите й, независещ от броя на елементите в нея, се казва, че те притежават свойството random access (свободен достъп). Такова свойство обикновено се наблюдава при реализации на абстрактни структури от данни с хеш-таблици и масиви.
Какво е хеш-таблица?
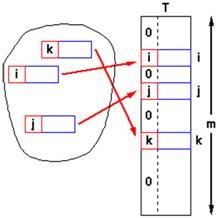
Структурата от данни хеш-таблица обикновено се реализира с масив. Тя съдържа наредени двойки (ключ, стойност), които са разположени в масива на пръв поглед случайно и непоследователно. В позициите, в които нямаме наредена двойка, имаме празен елемент (null):
Размерът на таблицата (масива), наричаме капацитет (capacity) на хеш-таблицата. Степен на запълненост (load factor), наричаме реално число между 0 и 1, което съответства на отношението между броя на запълнените елементи и текущия капацитет. На фигурата имаме хеш-таблица с 3 елемента и капацитет m. Следователно степента на запълване на тази хеш-таблица е 3/m.
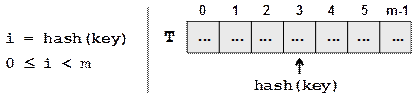
Добавянето и търсенето на елементи става, като върху ключа се приложи някаква функция hash(key), която връща число, наречено хеш-код. Като вземем остатъка при деление на този хеш-код с капацитета m получаваме число между 0 и m-1:
|
index = hash(key) % m |
На фигурата е показана хеш-таблица T с капацитет m и хеш-функция hash(key):
Това число ни дава позицията, на която да търсим или добавяме наредената двойка. Ако хеш-функцията разпределя ключовете равномерно, в болшинството случаи на различен ключ ще съответства различна хеш-стойност и по този начин във всяка клетка от масива ще има най-много един ключ. В крайна сметка получаваме изключително бързо търсене и бързо добавяне. Разбира се, може да се случи различни ключове да имат един и същ хеш-код. Това е специален случай, който ще разгледаме след малко.
|
Използвайте реализация на речник чрез хеш-таблици, когато се нуждаете от максимално бързо намиране на стойностите по ключ. |
Капацитетът на таблицата се увеличава, когато броят на наредените двойки в хеш-таблицата стане равен или по-голям от дадена константа, наречена максимална степен на запълване. При разширяване на капацитета (най-често удвояване) всички елементи се преподреждат според своя хеш-код и стойността на новия капацитет. Степента на запълване след преподреждане значително намалява. Операцията е времеотнемаща, но се извършва достатъчно рядко, за да не влияе на цялостната производителност на операцията добавяне.
Класът Dictionary<K, V>
Класът Dictionary<K, V> е стандартна имплементация на речник с хеш-таблица в .NET Framework. В следващите точки ще разгледаме основните операции, които той предоставя. Ще разгледаме и един конкретен пример, илюстриращ използването на класа и неговите методи.
Основни операции с класа Dictionary<K, V>
Създаването на хеш-таблица става чрез извикването на някои от конструкторите на Dictionary<K, V>. Чрез тях можем да зададем начални стойности за капацитет и максимална степен на запълване. Добре е, ако предварително знаем приблизителният брой на елементите, които ще бъдат добавени в нашата хеш-таблица, да го укажем още при създаването й. Така ще избегнем излишното разширяване на таблицата и ще постигнем по-добра ефективност. По подразбиране стойността на началния капацитет е 16, а на максималната степен на запълване е 0.75.
Да разгледаме какво прави всеки един от методите реализирани в класа Dictionary<K, V>:
- void Add(K, V) добавя нова стойност за даден ключ. При опит за добавяне на ключ, който вече съществува в речника, се хвърля изключение. Операцията работи изключително бързо.
- bool TryGetValue(K, out V) връща елемент от тип V чрез out параметър за дадения ключ или null, ако няма елемент с такъв ключ. Резултатът от изпълнението на метода е true ако е намерен елемент. Операцията е много бърза, тъй като алгоритъмът за търсене на елемент по ключ в хеш-таблица се доближава по сложност до O(1)
- bool Remove(K) изтрива от речника елемента с този ключ. Операцията работи изключително бързо.
- void Clear() премахва всички елементи от речника.
- bool ContainsKey(K) проверява дали в речника присъства наредена двойка с посочения ключ. Операцията работи изключително бързо.
- bool ContainsValue(V) проверява дали в речникa присъстват една или повече наредени двойки с посочената стойност. Тази операция работи бавно, тъй като проверява всеки елемент на хеш-таблицата.
- int Count връща броя на наредените двойки в речника.
- Други операции – например извличане на всички ключове, стойности или наредени двойки в структура, която може да бъде обходена чрез цикъл.
Студенти и оценки – пример
Ще илюстрираме как се използват някои от описаните по-горе операции чрез един пример. Нека имаме студенти, като всеки от тях би могъл да има най-много една оценка. Искаме да съхраняваме оценките в някаква структура, в която можем бързо да търсим по име на студент.
За тази задача ще създадем хеш-таблица с начален капацитет 6. Тя ще има за ключове имената на студентите, а за стойности – някакви техни оценки. Добавяме 6 примерни студента, след което наблюдаваме какво се случва когато отпечатваме на стандартния изход техните данни. Ето как изглежда кодът от този пример:
|
using System; using System.Collections.Generic; class StudentsExample { static void Main() { IDictionary<string, double> studentMarks = new Dictionary<string, double>();
studentMarks["Pesho"] = 3.00; studentMarks["Gosho"] = 4.50; studentMarks["Nakov"] = 5.50; studentMarks["Vesko"] = 3.50; studentMarks["Tsanev"] = 4.00; studentMarks["Nerdy"] = 6.00;
double tsanevMark = studentMarks["Tsanev"]; Console.WriteLine("Tsanev's mark: {0:0.00}", tsanevMark);
studentMarks.Remove("Tsanev"); Console.WriteLine("Tsanev's mark removed.");
Console.WriteLine("Is Tsanev in the dictionary: {0}", studentMarks.ContainsKey("Tsanev") ? "Yes!": "No!");
Console.WriteLine("Nerdy's mark is {0:0.00}.", studentMarks["Nerdy"]); studentMarks["Nerdy"] = 3.25; Console.WriteLine( "But we all know he deserves no more than {0:0.00}.", studentMarks["Nerdy"]);
double mishosMark; bool findMisho = studentMarks.TryGetValue("Misho", out mishosMark);
Console.WriteLine( "Is Misho's mark in the dictionary? {0}", findMisho ? "Yes!": "No!");
studentMarks["Misho"] = 6.00; findMisho = studentMarks.TryGetValue("Misho", out mishosMark);
Console.WriteLine( "Let's try again: {0}. Misho's mark is {1}", findMisho ? "Yes!" : "No!", mishosMark);
Console.WriteLine("Students and marks:");
foreach (KeyValuePair<string, double> studentMark in studentMarks) { Console.WriteLine("{0} has {1:0.00}", studentMark.Key, studentMark.Value); }
Console.WriteLine( "There are {0} students in the dictionary", studentMarks.Count); studentMarks.Clear(); Console.WriteLine("Students dictionary cleared."); Console.WriteLine("Is dictionary empty: {0}", studentMarks.Count == 0);
Console.ReadLine(); } } |
Изходът от изпълнението на този код е следният:
|
Tsanev's mark: 4.00 Tsanev's mark removed. Is Tsanev in the dictionary: No! Nerdy's mark is 6.00. But we all know he deserves no more than 3.25. Is Misho's mark in the dictionary? No! Let's try again: Yes!. Misho's mark is 6 Students and marks: Pesho has 3.00 Gosho has 4.50 Nakov has 5.50 Vesko has 3.50 Misho has 6.00 Nerdy has 3.25 There are 6 students in the dictionary Students dictionary cleared. Is dictionary empty: True |
Виждаме, че няма подредба при отпечатването на студентите. Това е така, защото при хеш-таблиците (за разлика от балансираните дървета) елементите не се пазят сортирани. Дори ако текущият капацитет на таблицата се промени докато работим с нея, много е вероятно да се промени и редът, в който се пазят наредените двойки. Причината за това поведение ще анализираме по-долу.
Важно е да се запомни, че при хеш-таблиците не можем да разчитаме на никаква наредба на елементите. Ако се нуждаем от такава, можем преди отпечатване да сортираме елементите. Друг вариант е да използваме SortedDictionary<K, V>.
Хеш-функции и хеширане
Сега ще се спрем по-детайлно на понятието, хеш-код, което употребихме малко по-рано. Хеш-кодът представлява числото, което ни връща т.нар. хеш-функция, приложена върху ключа. Това число трябва да е различно за всеки различен ключ или поне с голяма вероятност при различни ключове хеш-кодът трябва да е различен.
Хеш-функции
Съществува понятието перфектна хеш-функция (perfect hash function). Една хеш-функция се нарича перфектна, ако при N ключа, на всеки ключ функцията съпоставя различно цяло число в някакъв смислен интервал (например от 0 до N-1). Намирането на такава функция в общия случай е доста трудна, почти невъзможна задача. Такива функции си струва да се използват само при множества от ключове, които са с предварително известни елементи или поне ако множеството от ключове рядко се променя.
В практиката се използват други, не чак толкова "перфектни" хеш-функции.
Сега ще разгледаме няколко примера за хеш-функции, които се използват директно в .NET библиотеките.
Методът GetHashCode() в .NET платформата
Всички .NET класове имат метод GetHashCode(), който връща стойност от тип int. Този метод се наследява от класа Оbject, който стои в корена на йерархията на всички .NET класове.
Имплементацията в класа Object на метода GetHashCode() e такава, че не се гарантира уникалността на резултата. Това означава, че класовете наследници трябва да осигурят имплементация на GetHashCode() за да се ползват за ключ на хеш-таблица.
Друг пример за хеш-функция, която идва директно в .NET, е използваната от класовете int, byte и short (дефиниращи целите числа). Там за хеш-код се ползва стойността на самото число.
Един по-сложен пример за хеш-функция е имплементацията на класа string:
|
public override unsafe int GetHashCode() { fixed (char* str = ((char*)this)) { char* chPtr = str; int num = 352654597; int num2 = num; int* numPtr = (int*)chPtr; for (int i = this.Length; i > 0; i -= 4) { num = (((num << 5) + num) + (num >> 27)) ^ numPtr[0]; if (i <= 2) { break; } num2 = (((num2 << 5) + num2) + (num2 >> 27)) ^ numPtr[1]; numPtr += 2; } return (num + (num2 * 1566083941)); } } |
Имплементацията е доста сложна, но това, което трябва да запомним е, че тя гарантира уникалността на резултата точно когато низовете са различни. Още нещо което може да забележим е, че сложността на алгоритъма за изчисляване на хеш-кода на string е пропорционална на Length / 4 или O(n), което означава, че колкото по-дълъг е низа толкова по-бавно ще се изчислява неговия хеш-код.
На читателя оставяме да разгледа други имплементации на метода GetHashCode() в някои от най-често използваните класове като Date, long, float и double.
Сега, нека се спрем на въпроса как да имплементираме сами този метод за нашите класове. Вече обяснихме, че оставянето на имплементацията, която идва наготово от object, не е допустимо решение. Друга много проста имплементация е винаги да връщаме някаква фиксирана константа, примерно:
|
public override int GetHashCode() { return 42; } |
Ако в хеш-таблица използваме за ключове обекти от клас, който има горната имплементация на GetHashCode(), ще получим много лоша производителност, защото всеки път, когато добавяме нов елемент в таблицата, ще трябва да го слагаме на едно и също място. Когато търсим, всеки път ще попадаме в една и съща клетка на таблицата.
За да се избягва описаното неблагоприятно поведение, трябва хеш-функцията да разпределя ключовете равномерно сред възможните стойности за хеш-код.
Колизии при хеш-функциите
Ситуация, при която два различни ключа връщат едно и също число за хеш-код наричаме колизия:
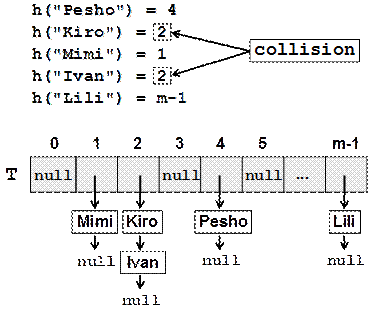
Как да решим проблема с колизиите ще разгледаме подробно в следващия параграф. Най-простото решение, обаче е очевидно: двойките, които имат ключове с еднакви хеш-кодове да нареждаме в списък:
Следователно при използване на константа 42 за хеш-код, нашата хеш-таблица се изражда в линеен списък и употребата й става неефективна.
Имплементиране на метода GetHashCode()
Ще дадем един стандартен алгоритъм, по който можем сами да имплементираме GetHashCode(), когато ни се наложи:
Първо трябва да определим полетата на класа, които участват по някакъв начин в имплементацията на Equals(object) метода. Това е необходимо, тъй като винаги, когато Equals() е true трябва резултатът от GetHashCode() да е един и същ. Така полетата, които не участват в пресмятането на Equals(), не трябва да участват и в изчисляване на GetHashCode().
След като сме определили полетата, които ще участват в изчислението на GetHashCode(), трябва по някакъв начин да получим за тях стойности от тип int. Ето една примерна схема:
- Ако полето е bool, за true взимаме 1, а за false взимаме 0 (или директно викаме GetHashCode() на bool).
- Ако полето е от тип int, byte, short, char можем да го преобразуваме към int, чрез оператора за явно преобразуване (int) (или директно викаме GetHashCode()).
- Ако полето е от тип long, float или double, можем да ползваме наготово резултата от техните GetHashCode().
- Ако полето не е от примитивен тип, просто извикваме метода GetHashCode() на този обект. Ако стойността на полето е null, връщаме 0.
- Ако полето е масив или някаква колекция, извличаме хеш-кода за всеки елемент на тази колекция.
Накрая сумираме получените int стойности, като преди всяко събиране умножаваме временния резултат с някое просто число (например 83), като игнорираме евентуалните препълвания на типа int.
В крайна сметка получаваме хеш-код, който е добре разпределен в пространството от всички 32-битови стойности. Можем да очакваме, че при така изчислен хеш-код колизиите ще са рядкост, тъй като всяка промяна в някое от полетата, участващи в описаната схема за изчисление, води до съществена промяна в хеш-кода.
Имплементиране на GetHashCode() – пример
Да илюстрираме горният алгоритъм с един пример. Нека имаме клас, чиито обекти представляват точка в тримерното пространство. И нека точката вътрешно представяме чрез нейните координати по трите измерения x, y и z:
|
Point3D.cs |
|
/// <summary> /// Class representing a point in three dimensional space. /// </summary> public class Point3D { private double x; private double y; private double z;
/// <summary> /// Constructs a new <see cref="Point3D"/> instance /// with the specified Cartesian coordinates of the point. /// </summary> /// <param name="x">x coordinate of the point</param> /// <param name="y">y coordinate of the point</param> /// <param name="z">z coordinate of the point</param> public Point3D(double x, double y, double z) { this.x = x; this.y = y; this.z = z; } } |
Можем лесно да реализираме GetHashCode() по описания по-горе алгоритъм:
|
... { if (this == obj) return true;
Point3D other = obj as Point3D;
if (other == null) return false;
if (!this.x.Equals(other.x)) return false;
if (!this.y.Equals(other.y)) return false;
if (!this.z.Equals(other.z)) return false;
return true; }
public override int GetHashCode() { int prime = 83; int result = 1; unchecked { result = result * prime + x.GetHashCode(); result = result * prime + y.GetHashCode(); result = result * prime + z.GetHashCode(); } return result; } } |
Тази имплементация е несравнимо по-добра, от това да не правим нищо или да връщаме константа. Въпреки това колизиите и при нея се срещат, но доста по-рядко.
Интерфейсът IEqualityComparer<T>
Едно от най-важните неща, които разбрахме досега е, че за да ползваме инстанциите на даден клас като ключове за речник, то класа трябва да имплементира правилно GetHashCode и Equals. Но какво да направим, ако искаме да използваме клас, който не можем или не искаме да наследим или променим? В този случай на помощ идва интерфейсът IEqualityComparer<T>. Той дефинира следните две операции:
bool Equals(T obj1, T obj2) – връща true ако obj1 и obj2 са равни
int GetHashCode(T obj) – връща хеш-кода за дадения обект.
Вече се досещате, че речниците в .NET могат да използват инстанция на IEqualityComparer, вместо съответните методи на класа даден за ключ. По този начин разработчиците могат да ползват практически всеки клас за ключ на речник, стига да осигурят имплементация на IEqualityComparer за този клас. Дори нещо повече - когато предоставим IEqualityComparer на речник, можем да променим начина, по който се изчислява GetHashCode и Equals за всякакви типове, дори за тези в .NET, тъй като в този случай речника използва методите на интерфейса вместо съответните методи на класа ключ. Ето един пример за имплементация на IEqualityComparer, за класа Point3D, който разгледахме по-рано:
|
public class Point3DEqualityComparer : IEqualityComparer<Point3D> {
#region IEqualityComparer Members
public bool Equals(Point3D point1, Point3D point2) { if (point1 == point2) return true;
if (point1 == null ^ point2 == null) return false;
if (!point1.X.Equals(point2.X)) return false;
if (!point1.Y.Equals(point2.Y)) return false;
if (!point1.Z.Equals(point2.Z)) return false;
return true; }
public int GetHashCode(Point3D obj) { Point3D point = obj as Point3D; if (point == null) { return 0; }
int prime = 83; int result = 1; unchecked { result = result * prime + point.X.GetHashCode(); result = result * prime + point.Y.GetHashCode(); result = result * prime + point.Z.GetHashCode(); } return result; }
#endregion } |
За да използваме Point3DЕqualityComparer е достатъчно единствено да го подадем като параметър на конструктора на нашия речник:
|
IEqualityComparer<Point3D> comparer = new Point3DEqualityComparer();
Dictionary<Point3D, int> dict = new Dictionary<Point3D, int>(comparer);
dict[new Point3D(1, 2, 3)] = 1; Console.WriteLine(++dict[new Point3D(1, 2, 3)]); |
Решаване на проблема с колизиите
На практика колизиите има почти винаги с изключение на много редки и специфични ситуации. За това е необходимо да живеем с идеята за тяхното присъствие в нашите хеш-таблици и да се съобразяваме с тях. Нека разгледаме няколко стратегии за справяне с колизиите:
Нареждане в списък (chaining)
Най-разпространеният начин за решаване на проблема с колизиите е нареждането в списък (chaining). Той се състои в това двойките ключ и стойност, които имат еднакъв хеш-код за ключа да се нареждат в списък един след друг.
Реализация на речник чрез хеш-таблица и chaining
Нека си поставим за задача да реализираме структурата от данни речник чрез хеш-таблица с решаване на колизиите чрез нареждане в списък (chaining). Да видим как може да стане това. Първо ще дефинираме клас, който описва наредената двойка (Key, Value):
|
KeyValuePair.cs |
|
public struct KeyValuePair<TKey, TValue> { private TKey key; private TValue value;
public KeyValuePair(TKey key, TValue value) { this.key = key; this.value = value; }
public TKey Key { get { return this.key; } } public TValue Value { get { return this.value; } } public override string ToString() { StringBuilder builder = new StringBuilder(); builder.Append('['); if (this.Key != null) { builder.Append(this.Key.ToString()); } builder.Append(", "); if (this.Value != null) { builder.Append(this.Value.ToString()); } builder.Append(']'); return builder.ToString(); } } |
Този клас има конструктор, който приема ключ от тип TKey и стойност от тип TValue. Дефинирани са два метода за достъп съответно за ключа (Key) и стойността (Value). Ще отбележим, че нарочно нямаме публични методи, чрез които да променяме стойностите на ключа и стойността. Това прави този клас непроменяем (immutable). Това е добра идея, тъй като обектите, които ще се пазят вътрешно в реализациите на речника, ще бъдат същите като тези, които ще връщаме например при реализацията на метод за вземане на всички наредени двойки.
Предефинирали сме метода ToString(), за да можем лесно да отпечатваме наредената двойка на стандартния изход или в текстов файл.
Следва примерен шаблонен интерфейс, който дефинира най-типичните операции за типа речник:
|
Idictionary.cs |
|
using System; using System.Collections.Generic; /// <summary> /// Interface that defines basic methods needed /// for a class which maps keys to values. /// </summary> /// <typeparam name="K">Key type</typeparam> /// <typeparam name="V">Value type</typeparam> public interface IDictionary<K, V> : IEnumerable<KeyValuePair<K, V>> {
/// <summary> /// Adds the specified value by the specified /// key to the dictionary. If the key already /// exists its value is replaced with the /// new value and the old value is returned. /// </summary> /// <param name="key">Key for the new value</param> /// <param name="value">Value to be mapped /// with that key</param> /// <returns>the old value for the specified /// key or null if the key does not exist</returns> /// <exception cref="NullReferenceException"> /// If Key is null</exception> V Set(K key, V value);
///<summary> /// Finds the value mapped by specified key. ///</summary> /// <param name="key">key for which the value /// is needed.</param> /// <returns>value for the specified key if present, /// or null if there is no value with such key</returns> V Get(K key);
/// <summary> /// Gets or sets the value of the entry in the /// dictionary identified by the Key specified. /// </summary> /// <remarks>A new entry will be created if the /// value is set for a key that is not currently /// in the Dictionary</remarks> /// <param name="key">Key to identify the entry /// in the Dictionary</param> /// <returns>Value of the entry in the Dictionary /// identified by the Key provided</returns> V this[K key] { get; set; }
/// <summary> /// Removes an element in the Dictionary /// identified by a specified key. /// </summary> /// <param name="key">Key to identify the /// element in the Dictionary to be removed</param> /// <returns></returns> bool Remove(K key);
/// <summary> /// Get a value indicating the number of /// entries in the Dictionary /// </summary> /// <returns></returns> int Count { get; }
/// <summary> /// Removes all the elements from the dictionary. /// </summary> void Clear(); } |
В интерфейса по-горе, както и в предходния клас използваме шаблонни типове (generics), чрез които декларираме параметри за типа на ключовете (K) и типа на стойностите (V). Това позволява нашият речник да бъде използван с произволни типове за ключовете и за стойностите. Както вече знаем, единственото изискване е ключовете да дефинират коректно методите Equals() и GetHashCode().
Нашият интерфейс IDictionary<K, V> прилича много на интерфейса System.Collections.Generic.IDictionary<K, V>, но е по-прост от него и описва само най-важните операции върху типа данни "речник". Той наследява системния интерфейс IEnumerable<DictionaryEntry<K, V>>, за да позволи речникът да бъде обхождан във for цикъл.
Следва примерна имплементация на речник, при който проблемът с колизиите се решава чрез нареждане в списък (chaining):
|
HashDictionary.cs |
|
/// <summary> /// Implementation of <see cref="IDictionary"/> interface /// using hash table. Collisions are resolved by chaining. /// </summary> /// <typeparam name="K">Type of the keys</typeparam> /// <typeparam name="V">Type of the values</typeparam> public class HashDictionary<K, V>:IEnumerable<KeyValuePair<K, V>> { private const int DEFAULT_CAPACITY = 2; private const float DEFAULT_LOAD_FACTOR = 0.75f; private List<KeyValuePair<K, V>>[] table; private float loadFactor; private int threshold; private int size; private int initialCapacity;
public HashDictionary() :this(DEFAULT_CAPACITY, DEFAULT_LOAD_FACTOR) { }
private HashDictionary(int capacity, float loadFactor) { this.initialCapacity = capacity; this.table = new List<KeyValuePair<K, V>>[capacity]; this.loadFactor = loadFactor; unchecked { this.threshold = (int)(capacity * this.loadFactor); } }
public void Clear() { if (this.table != null) { this.table = new List<KeyValuePair<K, V>>[initialCapacity]; } this.size = 0; }
private List<KeyValuePair<K, V>> FindChain( K key, bool createIfMissing) { int index = key.GetHashCode(); index = index % this.table.Length; if (this.table[index] == null && createIfMissing) { this.table[index] = new List<KeyValuePair<K, V>>(); } return this.table[index] as List<KeyValuePair<K, V>>; }
public V Get(K key) { List<KeyValuePair<K, V>> chain = this.FindChain(key, false); if (chain != null) { foreach (KeyValuePair<K, V> entry in chain) { if (entry.Key.Equals(key)) { return entry.Value; } } }
return default(V); }
public V this[K key] { get { return this.Get(key); } set { this.Set(key, value); } }
public int Count { get { return this.size; } }
public V Set(K key, V value) { List<KeyValuePair<K, V>> chain = this.FindChain(key, true);
for (int i = 0; i < chain.Count; i++) { KeyValuePair<K, V> entry = chain[i]; if (entry.Key.Equals(key)) { // Key found -> replace its value //with the new value KeyValuePair<K, V> newEntry = new KeyValuePair<K, V>(key, value); chain[i] = newEntry; return entry.Value; } } chain.Add(new KeyValuePair<K, V>(key, value)); if (size++ >= threshold) { this.Expand(); }
return default(V); }
/// <summary> /// Expands the underling table /// </summary> private void Expand() { int newCapacity = 2 * this.table.Length; List<KeyValuePair<K, V>>[] oldTable = this.table; this.table = new List<KeyValuePair<K, V>>[newCapacity]; this.threshold = (int)(newCapacity * this.loadFactor); foreach (List<KeyValuePair<K, V>> oldChain in oldTable) { if (oldChain != null) { foreach (KeyValuePair<K, V> keyValuePair in oldChain) { List<KeyValuePair<K, V>> chain = FindChain(keyValuePair.Key, true); chain.Add(keyValuePair); } } } }
public bool Remove(K key) { List<KeyValuePair<K, V>> chain = this.FindChain(key, false);
if (chain != null) { for (int i = 0; i < chain.Count; i++) { KeyValuePair<K, V> entry = chain[i]; if (entry.Key.Equals(key)) { // Key found -> remove it chain.RemoveAt(i); return true; } } } return false; }
IEnumerator<KeyValuePair<K, V>> IEnumerable<KeyValuePair<K, V>>.GetEnumerator() { foreach (List<KeyValuePair<K, V>> chain in this.table) { if (chain != null) { foreach (KeyValuePair<K, V> entry in chain) { yield return entry; } } } }
IEnumerator IEnumerable.GetEnumerator() { return ((IEnumerable<KeyValuePair<K, V>>)this). GetEnumerator(); } } |
Ще обърнем внимание на по-важните моменти в този код. Нека започнем от конструктора. Единственият публичен конструктор е конструкторът по подразбиране. Той в себе си извиква друг конструктор като му подава някакви предварително зададени стойности за капацитет и степен на запълване. На читателя предоставяме да реализира валидация на тези параметри и да направи и този конструктор публичен, за да предостави повече гъвкавост на ползвателите на този клас.
Следващото нещо, на което ще обърнем внимание, е това как е реализирано нареждането в списък. При конструирането на хеш-таблицата в конструктора инициализираме масив от списъци, които ще съдържат нашите KeyValuePair обекти. За вътрешно ползване сме реализирали един метод FindChain(), който изчислява хеш-кода на ключа като вика метода GetHashCode() и след това разделя върнатата хеш-стойност на дължината на таблицата (капацитета). Така се получава индексът на текущия ключ в масива, съхраняващ елементите на хеш-таблицата. Списъкът с всички елементи, имащи съответния хеш-код, се намира в масива на изчисления индекс. Ако списъкът е празен, той има стойност null. В противен случай в съответната позиция има списък от елементи за съответния ключ.
На метода FindChain() се подава специален параметър, който указва дали да създава празен списък, ако за подадения ключ все още няма списък с елементи. Това предоставя удобство на методите за добавяне на елементи и за преоразмеряване на хеш-таблицата.
Другото нещо, на което ще обърнем внимание, е методът Expand(), който разширява текущата таблица, когато се достигне максималното допустимо запълване. За целта създаваме нова таблица (масив), двойно по-голяма от старата. Изчисляваме новото максимално допустимо запълване, това е полето threshold. Следва най-важната част. Разширили сме таблицата и по този начин сме сменили стойността на this.table.Length. Ако потърсим някой елемент, който вече сме добавили, методът FindChain(K key), изобщо няма да върне правилната верига, в която да го търсим. Затова се налага всички елементи от старата таблица да се прехвърлят, като не просто се копират веригите, а се добавят наново обектите от клас KeyValuePair в новосъздадени вериги.
За да имплементираме коректно обхождането на хеш-таблицата, реализирахме интерфейса IEnumerable<KeyValuePair<K, V>>, който има метод GetEnumerator(), връщащ итератор (IEnumerator) по елементите на хеш-таблицата, който в случая за улеснение реализирахме чрез израза yield return. След малко ще дадем пример как можем да използваме нашата реализация на хеш-таблица и нейният итератор. Но първо, за да тестваме по-лесно всичките им аспекти, нека направим малка промяна в имплементацията на Point3D, която разгледахме по-рано и по-точно в това как се изчислява хеш-кода:
|
/// <summary> /// Class representing a point in three dimensional space. /// </summary> public class Point3D { private double x; private double y; private double z;
/// <summary> /// Constructs a new <see cref="Point3D"/> instance /// with the specified Cartesian coordinates of the point. /// </summary> /// <param name="x">x coordinate of the point</param> /// <param name="y">y coordinate of the point</param> /// <param name="z">z coordinate of the point</param> public Point3D(double x, double y, double z) { this.x = x; this.y = y; this.z = z; }
public double X { get { return x; } set { x = value; } }
public double Y { get { return y; } set { y = value; } }
public double Z { get { return z; } set { z = value; } }
public override bool Equals(object obj) { if (this == obj) return true;
Point3D other = obj as Point3D;
if (other == null) return false;
if (!this.x.Equals(other.x)) return false;
if (!this.y.Equals(other.y)) return false;
if (!this.z.Equals(other.z)) return false;
return true; }
public override int GetHashCode() { //int prime = 83; //int result = 1; //unchecked //{ // result = result * prime + x.GetHashCode(); // result = result * prime + y.GetHashCode(); // result = result * prime + z.GetHashCode(); //}
int result = (int)Math.Round((x + y + z));
return result; }
public override string ToString() { return string.Format("X={0} Y={1} Z={2}", x, y, z); } } |
В този случай използваме много примитивен подход за генериране на хеш-код, който в случая ще ни помогне да тестваме колизиите в нашата хеш-таблица. Следва примерът, който ползва HashDictionary и модифицираната версия на Point3D:
|
class Program { static void Main() { HashDictionary<Point3D, int> dict = new HashDictionary<Point3D, int>();
dict[new Point3D(1, 2, 3)] = 1; //Set value Console.WriteLine(dict[new Point3D(1, 2, 3)]); //Get value
//Set Value, overwrite previous value for the same Key dict[new Point3D(1, 2, 3)] += 1; Console.WriteLine(dict[new Point3D(1, 2, 3)]);
//Now this Point has the same HashCode as the previos one dict[new Point3D(3, 2, 1)] = 42;
Console.WriteLine(dict[new Point3D(3, 2, 1)]); //test if chaining works and elements with equal //hashcodes are not overwritten Console.WriteLine(dict[new Point3D(1, 2, 3)]);
//HashCode to test the creation of another entry //in the internal table dict[new Point3D(1001, 100, 10)] = 1111; Console.WriteLine(dict[new Point3D(1001, 100, 10)]);
//iterate through the Dictionary entries and print values foreach (KeyValuePair<Point3D, int> entry in dict) { Console.WriteLine( "Key: " + entry.Key + "; Value: " + entry.Value); } } } |
Както очаквате, резултатът от изпълнението на програмата е следният:
|
1 2 42 2 1111 Key: X=1 Y=2 Z=3; Value: 2 Key: X=3 Y=2 Z=1; Value: 42 Key: X=1001 Y=100 Z=10; Value: 1111 |
В примерната имплементация на хеш-таблица има още една особеност. Методът FindChain() не е реализиран напълно коректно. В повечето случаи тази реализация ще работи без проблем, но какво ще стане, ако добавяме елементи до безкрай? В един прекрасен момент, когато капацитетът е станал 231 и се наложи да го разширим, то при умножение на това число с 2 ще получим -2 (вж. секцията за представяне на отрицателни числа в главата "Бройни системи"). След това при опит за създаване на нов масив с размер -2 естествено ще бъде хвърлено изключение и изпълнението на метода ще бъде прекратено. Нека не лишаваме читателя от удоволствието да прецени как да се справи с тази задача.
Методи за решаване на колизиите от тип отворена адресация (open addressing)
Нека сега разгледаме методите за разрешаване на колизиите, алтернативни на нареждането в списък. Най-общо идеята при тях е, че в случай на колизия се опитваме да сложим новата двойка на някоя свободна позиция от таблицата. Методите се различават по това как се избира къде да се търси свободно място за новата двойка. Освен това трябва да е възможно и намирането на тази двойка на новото й място.
Основен недостатък на този тип методи спрямо нареждането в списък е, че са неефективни при голяма степен на запълненост (близка до 1).
Линейно пробване (linear probing)
Този метод е един от най-лесните за имплементация. Линейното пробване най-общо представлява следният простичък код:
|
int newPosition = (oldPosition + i) % capacity; |
Тук capacity е капацитетът на таблицата, oldPostion е позицията, за която получаваме колизия, а i е номер на поредното пробване. Ако новополучената позиция е свободна, то мястото се използва за новодобавената двойка, в противен случай пробваме отново, като увеличаваме i с единица. Възможно е пробването да е както напред така и назад. Пробване назад става като вместо да прибавяме, вадим i от позицията, в която имаме колизия.
Предимство на този метод е сравнително бързото намиране на нова позиция. За нещастие има изключително висока вероятност, ако на едно място е имало колизия, след време да има и още. Това на практика води до силна неефективност.
|
Използването на линейно пробване като метод за решаване на проблема с колизиите е неефективно и трябва да се избягва. |
Квадратично пробване (Quadratic probing)
Това е класически метод за решаване на проблема с колизиите. Той се различава от линейното пробване с това, че за намирането на нова позиция се използва квадратна функция на i (номер на поредно пробване). Ето как би изглеждало едно такова решение:
|
int newPosition = (oldPosition + c1*i + c2*i*i) % capacity; |
Тук се появяват две константи c1 и c2. Иска се c2 да е различна от 0, защото в противен случай се връщаме на линейно пробване.
От избора на c1 и c2 зависи на кои позиции спрямо началната ще пробваме. Например, ако c1 и c2 са равни на 1, ще пробваме последователно oldPosition, oldPosition + 2, oldPosition + 6, …. За таблица с капацитет от вида 2n, е най-добре да се изберат c1 и c2 равни на 0.5.
Квадратичното пробване е по-ефективно от линейното.
Двойно хеширане (double hashing)
Както става ясно и от името на този метод, при повторното хеширане за намиране на нова позиция се прави повторно хеширане на получения хеш-код, но с друга хеш-функция, съвсем различна от първата. Този метод е по-добър от линейното и квадратичното пробване, тъй като всяко следващо пробване зависи от стойността на ключа, а не от позицията определена за ключа в таблицата. Това има смисъл, защото позицията за даден ключ зависи от текущия капацитет на таблицата.
Кукувиче хеширане (cuckoo hashing)
Кукувичето хеширане е сравнително нов метод с отворена адресация за справяне с колизиите. Той е бил представен за пръв път от R. Pagh и F. Rodler през 2001 година. Името му идва от поведението, наблюдавано при някои видове кукувици. Майките кукувици избутват яйца и/или малките на други птици извън гнездото им, за да оставят техните яйца там и така други птици да се грижат за техните яйца (и малки след излюпването).
Основната идея на този метод е да се използват две хеш-функции вместо една. По този начин ще разполагаме не с една, а с две позиции, на които можем да поставим елемент в речника. Ако единият от двата елемента е свободен, то просто слагаме елемента на свободна позиция. Ако пък и двете позиции са заети, то слагаме новият елемент на една от двете позиции, като той "изритва" елемента, който до сега се е намирал там. На свой ред "изритания" елемент отива на своята алтернативна позиция, като "изритва" някой друг елемент, ако е необходимо. Новият "изритан" повтаря процедурата и така, докато не се достигне свободна позиция или докато не се получи зацикляне. Във втория случай цялата таблица се построява наново с по-голям размер и с нови хеш-функции.
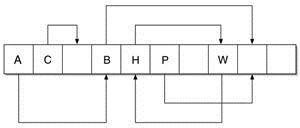
На картинката по-долу е показана примерна схема на хеш-таблица, която използва кукувиче хеширане. Всяка клетка, която съдържа елемент има връзка към алтернативната клетка за ключа, който се намира в нея. Сега ще проиграем различни ситуации за добавяне на нов елемент.
Ако поне една от двете хеш-функции ни даде свободна клетка, то няма проблем. Слагаме елемента в една от двете. Нека обаче и двете хеш-функции са дали заети клетки и на случаен принцип сме избрали една от тях.
Нека също предположим, че това е клетката, в която се намира A. Новият елемент изритва A от неговото място, A на свой ред отива на алтернативната си позиция и изритва B, от неговото място. Алтернативното място за B обаче е свободно, така че добавянето завършва успешно.
Да предположим, че клетката, от която се опитва да изрита елемент, новият елемент е тази, в която се намира H. Тогава се получава зацикляне тъй като H и W образуват цикъл. В този случай трябва да се изпълни пресъздаване на таблицата, използвайки нови хеш-функции и по-голям размер.
В най-опростената си версия този метод има константен достъп до елементите си и то в най-лошия случай, но това е изпълнено само при ограничението, че фактора на запълване е по-малък от 0.5.
Използването на три различни хеш-функции, вместо две може да доведе до ефективна горна граница на фактора на запълване до над 0.9.
Проучвания показват, че кукувичето хеширане и неговите варианти могат да бъдат много по-ефективни от широко използваните днес нареждане в списък и методите с отворено адресиране. Въпреки това все още този метод остава широко неизвестен и неизползван в практиката.
Структура от данни "множество"
В тази секция ще разгледаме абстрактната структура от данни множество (set) и две нейни типични реализации. Ще обясним предимствата и недостатъците им и в какви ситуации коя от имплементациите да предпочитаме.
Абстрактна структура данни "множество"
Множествата са колекции, в които няма повтарящи се елементи. В контекста на .NET това ще означава, че за всеки обект от множества извиквайки метода му Еquals(), като подаваме като аргумент някои от другите обекти в множеството резултатът винаги ще е false.
Някои множества позволяват присъствието в себе си и на null, други не.
Освен, че не допуска повтарящи се обекти, друго важно нещо, което отличава множеството от списъците и масивите е, че неговите елементи си нямат номер. Елементите на множеството не могат да бъдат достъпвани по някакъв друг ключ, както е при речниците. Самите елементи играят ролята на ключ.
Единственият начин да достъпите обект от множество е като разполагате със самия обект или евентуално с обект, който е еквивалентен на него. Затова на практика достъпваме всички елементи на дадено множество наведнъж, докато го обхождаме в цикъл. Например чрез разширената конструкцията за for цикъл.
Основните операции, които се дефинират от структурата множество са следните:
- bool Add(element) – добавя в множеството зададен елемент, като ако вече има такъв елемент, връща false, а в противен случай true.
- bool Contains(element) – проверява дали множеството съдържа посочения елемент. Ако го има връща true, a в противен случай false.
- bool Remove(element) – премахва посочения елемент от множеството, ако съществува. Връща дали елементът е бил намерен.
- void Clear() – премахва всички елементи от множеството
- void IntersectWith(Set other) – в текущото множество остават само елементите от сечението на двете множества – това е множество, което съдържа всички елементи, които са едновременно и в едното и в другото множество.
- void UnionWith(Set other) – в текущото множество се натрупват елементите от обединението на двете множества – това е множество, което съдържа всички елементи, които са или в едното или в другото множество или и в двете.
- bool IsSubsetOf(Set other) – проверява дали текущото множество е подмножество на даденото множество. Връща true при положителен отговор и false при отрицателен
- bool IsSupersetOf(Set other) – проверява дали дадено множество е подмножество на текущото. Връща true при положителен отговор и false при отрицателен
- int Count – свойство което връща текущия брой на елементите в множеството
В .NET има една единствена публична имплементация на множество – това е класът HashSet<T> (assembly System.Core, namespace System.Collections.Generic). Този клас имплементира множество чрез хеш-таблица. Но ако потърсим в асемблитата на .NET ще забележим, че има и вътрешен (internal) клас, който имплементира множество чрез червено-черно дърво – TreeSet. За съжаление TreeSet не може да бъде използван. Ако разгледаме внимателно имплементацията на тези класове ще видим, че те всъщност представляват речници, при които елементът е едновременно ключ и стойност на наредената двойка. Естествено, когато е удобно да работим с множества, трябва да ги предпочитаме, пред това да използваме речник. В .NET 4.0 вече има интерфейс ISet<T>.
Реализация с хеш-таблица – клас HashSet<T>
Както вече споменахме, реализацията на множество с хеш-таблица в .NET е класът HashSet<T>. Този клас, подобно на Dictionary<K, V>, има конструктори, чрез които може да се зададат списък с елементи, както и имплементация на IEqualityComparer, за който споменахме по-рано. Те имат същият смисъл, защото тук отново използваме хеш-таблица
Ето един пример, който демонстрира използване на множества и описаните в предния параграф основни операции - обединение и сечение:
|
class StudentListExample { static void Main() { HashSet<string> aspNetStudents = new HashSet<string>(); aspNetStudents.Add("S. Nakov"); aspNetStudents.Add("V. Kolev"); aspNetStudents.Add("M. Valkov");
HashSet<string> silverlightStudents = new HashSet<string>(); silverlightStudents.Add("S. Guthrie"); silverlightStudents.Add("M. Valkov");
HashSet<string> allStudents = new HashSet<string>(); allStudents.UnionWith(aspNetStudents); allStudents.UnionWith(silverlightStudents);
HashSet<string> intersectStudents = new HashSet<string>(aspNetStudents); intersectStudents.IntersectWith(silverlightStudents);
Console.WriteLine("ASP.NET students: " + GetListOfStudents(aspNetStudents)); Console.WriteLine("Silverlight students: " + GetListOfStudents(silverlightStudents)); Console.WriteLine("All students: " + GetListOfStudents(allStudents)); Console.WriteLine( "Students in both ASP.NET and Silverlight: " + GetListOfStudents(intersectStudents)); }
static string GetListOfStudents(IEnumerable<string> students) { string result = string.Empty; foreach (string student in students) { result += student + ", "; }
if (result != string.Empty) { //remove the extra separator at the end result = result.TrimEnd(',', ' '); }
return result; } } |
Резултатът от изпълнението е:
|
ASP.NET students: S. Nakov, V. Kolev, M. Valkov Silverlight students: S. Guthrie, M. Valkov All students: S. Nakov, V. Kolev, M. Valkov, S. Guthrie Students in both ASP.NET and Silverlight: M. Valkov |
Обърнете внимание, че "M. Valkov" присъства и в двете множества, но в обединението се появява само веднъж. Това е така, защото, както знаем, един елемент може да се съдържа най-много веднъж в дадено множество.
Реализация с черно-червено дърво – клас TreeSet<T>
TreeSet<T> представлява множество, реализирано чрез червено-черно дърво. В допълнение, то има свойството, че в него елементите се пазят подредени по големина. Това е причината в него да можем да добавяме само елементи, които са сравними. Припомняме, че в .NET това обикновено означава, че обектите са от клас, който имплементира IComparable<T>. Но както вече споменахме, в .NET класът TreeSet<T> е internal и следователно не можем да го ползваме. Или поне не директно. За щастие можем доста лесно да направим TreeSet с основните операции обединение и сечение, като ползваме SortedDictionary<Т>. Ето и нашата реализация на TreeSet:
|
TreeSet.cs |
|
using System; using System.Collections.Generic; /// <summary> /// Class that represents ordered set, based on SortedDictionary /// </summary> /// <typeparam name="T">The type of the elements /// in the set</typeparam> public class TreeSet<T>: ICollection<T> { private SortedDictionary<T, bool> innerDictionary;
public TreeSet(IEnumerable<T> element): this() { foreach (T item in element) { this.Add(item); } }
public TreeSet() { this.innerDictionary = new SortedDictionary<T, bool>(); }
/// <summary> /// Adds an element to the set. /// </summary> /// <param name="element">element to add</param> /// <returns>true if the element has not been /// already added, false otherwise</returns> public bool Add(T element) { if (!innerDictionary.ContainsKey(element)) { this.innerDictionary[element] = true; return true; }
return false; }
/// <summary> /// Performs intersection of this set with the specified set /// </summary> /// <param name="other">Set to intersect with</param> public void IntersectWith(TreeSet<T> other) { List<T> elementsToRemove = new List<T>(Math.Min(this.Count, other.Count));
foreach (T key in this.innerDictionary.Keys) { if (!other.Contains(key)) { elementsToRemove.Add(key); } }
foreach (T elementToRemove in elementsToRemove) { this.Remove(elementToRemove); } }
/// <summary> /// Performs an union operation with another set /// </summary> /// <param name="other">The set to perform union with</param> public void UnionWith(TreeSet<T> other) { foreach (T key in other) { this.innerDictionary[key] = true; } }
#region ICollection<T> Members
void ICollection<T>.Add(T item) { this.Add(item); }
public void Clear() { this.innerDictionary.Clear(); }
public bool Contains(T item) { return this.innerDictionary.ContainsKey(item); }
public void CopyTo(T[] array, int arrayIndex) { this.innerDictionary.Keys.CopyTo(array, arrayIndex); }
public int Count { get { return this.innerDictionary.Count; } }
public bool IsReadOnly { get { return false; } }
public bool Remove(T item) { return this.innerDictionary.Remove(item); }
#endregion
#region IEnumerable<T> Members
public IEnumerator<T> GetEnumerator() { return this.innerDictionary.Keys.GetEnumerator(); }
#endregion
#region IEnumerable Members
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() { return innerDictionary.Keys.GetEnumerator(); }
#endregion } |
Ще демонстрираме работата с класа TreeSet<T> с един пример:
|
class Program { static void Main() { TreeSet<string> bandsIvanchoLikes = new TreeSet<string>( new[] { "manowar", "blind guardian", "dio", "grave digger", "kiss", "dream theater", "manowar", "megadeth", "dream theater", "dio", "judas priest", "manowar", "kreator", "blind guardian", "iron maiden", "accept", "dream theater" });
TreeSet<string> bandsMariikaLikes = new TreeSet<string>( new[] { "iron maiden", "dio", "accept", "manowar", "slayer", "megadeth", "dio", "manowar", "running wild", "grave digger", "accept", "kiss", "manowar", "iron maiden", "manowar", "judas priest", "iced earth", "manowar", "dio", "iron maiden", "manowar", "slayer" });
Console.WriteLine("Ivancho likes these bands: "); Console.WriteLine( GetCommaSeparatedList(bandsIvanchoLikes)); Console.WriteLine();
Console.WriteLine("Mariika likes these bands: "); Console.WriteLine( GetCommaSeparatedList(bandsMariikaLikes)); Console.WriteLine();
TreeSet<string> intersectBands = new TreeSet<string>(); intersectBands.UnionWith(bandsIvanchoLikes); intersectBands.IntersectWith(bandsMariikaLikes);
Console.WriteLine(string.Format( "Does Ivancho like Mariika? {0}", intersectBands.Count > 5 ? "Yes!" : "No!"));
Console.WriteLine( "Because Ivancho and Mariika both like: "); Console.WriteLine( GetCommaSeparatedList(intersectBands)); Console.WriteLine();
TreeSet<string> uniounBands = new TreeSet<string>(); uniounBands.UnionWith(bandsIvanchoLikes); uniounBands.UnionWith(bandsMariikaLikes);
Console.WriteLine( "All bands that Ivancho or Mariika like:"); Console.WriteLine( GetCommaSeparatedList(uniounBands)); }
static string GetCommaSeparatedList( IEnumerable<string> items) { string result = string.Empty;
int i = 1; foreach (string item in items) { result += item + ", "; if (i % 3 == 0) //3 elements on a line { result += Environment.NewLine; }
i++; }
if (result != string.Empty) { //remove the extra separators at the end result = result.TrimEnd(',', ' ', '\r', '\n'); }
return result; } } |
След изпълнението на програмата получаваме следния резултат:
|
Ivancho likes these bands: accept, blind guardian, dio, dream theater, grave digger, iron maiden, judas priest, kiss, kreator, manowar, megadeth
Mariika likes these bands: accept, dio, grave digger, iced earth, iron maiden, judas priest, kiss, manowar, megadeth, running wild, slayer
Do Ivancho and Mariika like each other? Yes! Because Ivancho and Mariika both like: accept, dio, grave digger, iron maiden, judas priest, kiss, manowar, megadeth
All bands that Ivancho or Mariika like: accept, blind guardian, dio, dream theater, grave digger, iced earth, iron maiden, judas priest, kiss, kreator, manowar, megadeth, running wild, slayer |
Това, което можем веднага да забележим е, че елементите в нашето множество, за разлика от HashSet са винаги подредени.
В .NET Framework версия 4.0 вече има клас SortedSet<T> и интерфейс ISet<T>. Можете да се запознаете с тяхната имплементация, използвайки някой от декомпилаторите, описани в секцията "Декомпилиране на код".
За читателя остава задачата, да разшири функционалността на множеството с други операции. Това, за което е важно да си дадем сметка, е че работата с множества е наистина лесна и проста. Ако познаваме добре тяхната структура и свойства, ще можем да ги използвате ефективно и на място.
Упражнения
1. Напишете програма, която брои колко пъти се среща всяко число в дадена редица от числа.
Пример: array = {3, 4, 4, 2, 3, 3, 4, 3, 2}
2 à 2 пъти
3 à 4 пъти
4 à 3 пъти
2. Напишете програма, която премахва всички числа, които се срещат нечетен брой пъти в дадена редица. Например, ако имаме началната редица {4, 2, 2, 5, 2, 3, 2, 3, 1, 5, 2, 6, 6, 6}, трябва да я редуцираме до редицата {5, 3, 3, 5}.
3. Напишете програма, която по даден текст във текстов файл, преброява колко пъти се среща всяка дума. Отпечатайте на конзолата всички думи и по колко пъти се срещат, подредени по брой срещания.
Пример: "This is the TEXT. Text, text, text – THIS TEXT! Is this the text?"
Резултат:
is à 2, the à 2, this à 3, text à 6
4. Реализирайте клас DictHashSet<Т>, базиран на класа HashDictionary <K, V>, който разгледахме по-горе.
5. Реализирайте хеш-таблица, която съхранява тройки стойности (ключ1, ключ2, стойност) и позволява бързо търсене по двойка ключове и добавяне на тройки стойности.
6. Реализирайте хеш-таблица, която позволява по даден ключ да съхраняваме повече от една стойност.
7. Реализирайте хеш-таблица, която използва "кукувиче хеширане" с 3 хеш-функции за разрешаване на колизиите.
8. Реализирайте структурата данни хеш-таблица в клас HashTable<K, T>. Пазете данните в масив от списъци от двойки ключ-стойност (LinkedList<KeyValuePair<K,T>>[]) с начален капацитет от 16 елемента. Когато хеш-таблицата достигне 75% от своя капацитет да се удвоява капацитета. Реализирайте следните операции: Add(key, value), Find(key)àvalue, Remove(key), Count, Clear(), this[], Keys. Реализирайте и итериране по елементите на хеш-таблицата с foreach.
9. Реализирайте структурата от данни "Set" в клас HashedSet<T>. Използвайте класа от предната задача HashTable<K, T>, за да пазите елементите. Имплементирайте всички стандартни операции за типа данни Set: Add(T), Find(T), Remove(T), Count, Clear(), обединение и сечение.
10. Дадени са три редици от числа, дефинирани чрез формулите:
- f1(0) = 1; f1(k) = 2*f1(k-1) + 3; f1 = {1, 5, 13, 29, …}
- f2(0) = 2; f2(k) = 3*f2(k-1) + 1; f2 = {2, 7, 22, 67, …}
- f3(0) = 2; f3(k) = 2*f3(k-1) - 1; f3 = {2, 3, 5, 9, …}
Напишете програма, която намира сечението и обединението на множествата от членовете на редиците в интервала [0; 100000]: f1 * f2; f1 * f3; f2 * f3; f1 * f2 * f3; f1 + f2; f1 + f3; f2 + f3; f1 + f2 + f3. Със символите + и * означаваме съответно обединение и сечение на множества.
11. * Дефинирайте клас TreeMultiSet<T>, който позволява да пазим съвкупност от елементи, подредени по големина и позволява повторения на някои от елементите. Реализирайте операциите добавяне на елемент, търсене на броя срещания на даден елемент, изтриване на елемент, итератор, намиране на най-малък / най-голям елемент, изтриване на най-малък / най-голям елемент. Реализирайте възможност за подаване на външен Comparer<T> за сравнение на елементите.
12. * Даден е списък с времената на пристигане и заминаване на всички автобуси от дадена автогара. Да се напише програма, която използвайки HashSet класa по даден интервал (начало, край) намира броя автобуси, които успяват да пристигнат и да напуснат автогарата. Пример:
Имаме данните за следните автобуси: [08:24-08:33], [08:20-09:00], [08:32-08:37], [09:00-09:15]. Даден е интервалът [08:22-09:05]. Броят автобуси, които идват и си тръгват в рамките на този интервал е 2.
13. * Дадена е редица P с цели числа (1 < P < 50 000) и число N. Щастлива под-редица в редицата P наричаме всяка съвкупност, състояща се от последователни числа от P, чиято сума е N. Да си представим, че имаме редицата S, състояща се от всички щастливи под-редици в P, подредени в намаляващ ред спрямо дължината им. Напишете програма, която извежда първите 10 елемента на S. Пример:
Имаме N=5 и редицата P={1, 1, 2, 1, -1, 2, 3, -1, 1, 2, 3, 5, 1, -1, 2, 3}.
Редицата S се състои от следните 13 под-редици на P:
- [1, -1, 2, 3, -1, 1]
- [1, 2, 1, -1, 2]
- [1, -1, 2, 3]
- [2, 3, -1, 1]
- [3, -1, 1, 2]
- [-1, 1, 2, 3]
- [1, -1, 2, 3]
- [1, 1, 2, 1]
- [5, 1, -1]
- [2, 3]
- [2, 3]
- [2, 3]
- [5]
Първите 10 елемента на P са дадени с удебелен шрифт.
Решения и упътвания
1. Използвайте Dictionary<TKey,TValue>
2. Използвайте Dictionary и ArrayList.
3. Използвайте Dictionary с ключ дума и стойност – броя срещания. След като преброите всички думи, сортирате речника по стойност.
4. Използвайте за ключ и за стойност една и съща стойност – елементът от множеството.
5. Използвайте хеш-таблица от хеш-таблици.
6. Ползвайте Dictionary<K, ArrayList<V>>.
7. Можете за първа хеш-функция да ползвате GetHashCode() % size, за втора да ползвате (GetHashCode () * 83 + 7) % size, a за трета – (GetHashCode () * GetHashCode () + 19) % size).
8. За да удвоите размера на вашата колекция, можете да заделите двойно по-голям масив и да прехвърлите елементите от стария в новия, след което да насочите референцията от стария масив към новия. За да имплементирате foreach оператора върху вашата колекция, имплементирайте интерфейса IEnumerable и във вашия метод GetEnumerator() да връщате съответния метод GetEnumerator()на масива от списъци. Можете да използвате и оператора yield.
9. Един вариант да решите задачата е, да използвате за ключ в хеш-таблицата елемента от множеството, а за стойност винаги true. Обединението и сечението ще извършвате с изцикляне по елементите на едното множество и проверка дали в едното множество има (съответно няма) елемента от другото множество.
10. Намерете всички членове на трите редици в посочения интервал и след това използвайки HashSet<int> реализирайте обединение и сечение на множества, след което направете исканите пресмятания.
11. Класът TreeMultiSet<T> можете да реализираме чрез SortedDictionary<K, int>, който пази броя срещания на всеки от ключовете.
12. Очевидното решение е да проверим всеки от автобусите дали пристига и си тръгва в посочения интервал. Според условието на задачата, обаче, трябва да ползваме класа HashSet.
Решението е такова: Можем да намерим множествата на всички автобуси, които пристигат след началния час и на всички автобуси, отпътуващи преди крайния час. Сечението на тези множества дава търсените автобуси. Ако TimeInterval е клас който съхранява разписанието на един автобус, сечението можем да намерим с HashSet< TimeInterval> при подходящо дефинирани GetHashCode() и Equals().
13. Първата идея за решаване на задачата е проста: с два вложени цикъла намираме всички щастливи под-редици на редицата P, след което ги сортираме по дължината им и накрая извеждаме първите 10. Това, обаче няма да работи добре, ако броят щастливи под-редици са десетки милиони.
Ще опишем една идея за по-ефективно решение. Ще използваме класа TreeMultiSet<T>. В него ще съхраняваме първите 10 под-редици от S, т.е. мулти-множество от щастливите под-редици на P, подредени по дължина в намаляващ ред. Когато имаме 10 под-редици в мулти-множеството и добавим нова 11-та под-редица, тя ще застане на мястото си заради Comparer-а, който сме дефинирали. След това можем веднага да изтрием последната под-редица от мулти-множеството, защото тя не е сред първите 10. Така във всеки един момент ще пазим текущите 10 най-дълги под-редици. По този начин ще консумираме много по-малко памет и ще избегнем сортирането накрая. Имплементацията няма да е лесна, така че отделете достатъчно време!
Демонстрации (сорс код)
Изтеглете демонстрационните примери към настоящата глава от книгата: Речници,хеш-таблици-и-множества-Демонстрации.zip.
Дискусионен форум
Коментирайте книгата и задачите в нея във: форума на софтуерната академия.
Коментирай
Трябва да сте влезнали, за да коментирате.