Глава 10. Рекурсия

В тази тема...

В настоящата тема ще се запознаем с рекурсията и нейните приложения. Рекурсията представлява мощна техника, при която един метод извиква сам себе си. С нея могат да се решават сложни комбинаторни задачи, при които с лекота могат да бъдат изчерпвани различнDи комбинаторни конфи­гурации. Ще ви покажем много примери за правилно и неправилно използване на рекурсия и ще ви убедим колко полезна може да е тя.

Съдържание

• Видео
• Презентация
• Мисловни карти
• В тази тема...
• Какво е рекурсия?
• Пример за рекурсия
• Пряка и косвена рекурсия
• Дъно на рекурсията
• Създаване на рекурсивни методи
• Рекурсивно изчисляване на факториел
• Рекурсия или итерация
• Имитация на N вложени цикъла
• Кога да използваме рекурсия и кога итерация?
• Използване на рекурсия – изводи
• Упражнения
• Решения и упътвания
• Демонстрации (сорс код)
• Дискусионен форум

Видео

Презентация

Мисловни карти

Какво е рекурсия?

Един обект наричаме рекурсивен, ако съдържа себе си или е дефиниран чрез себе си.

Рекурсия е програмна техника, при която даден метод извиква сам себе си при ре­ша­ването на определен проблем. Такива методи наричаме рекурсивни.

Рекурсията е програмна техника, чиято правилна употреба води до еле­гант­ни решения на определени проблеми. Понякога нейното използване може да опрости значително кода и да подобри четимостта му.

Пример за рекурсия

Нека разгледаме числата на Фибоначи. Това са членовете на следната редица:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Всеки член на редицата се получава като сума на предходните два. Пър­ви­те два члена по дефиниция са равни на 1, т.е. в сила е:

F₁ = F₂ = 1

F_i = F_i-1 + F_i-2 (за i > 2)

Изхождайки директно от дефиницията, можем да реализираме следния рекурсивен метод за намиране на n-тото число на Фибоначи:

static long Fib(int n) {       if (n <= 2)       {             return 1;       }       return Fib(n - 1) + Fib(n - 2); }

Този пример ни показва, колко проста и естествена може да бъде реали­за­цията на дадено решение с помощта на рекурсия.

От друга страна, той може да ни служи и като пример, колко трябва да сме внимателни при използването на рекурсия. Макар, че е интуитивно, текущото решение е един от класическите примери, когато използването на рекурсия е изключително неефективно, поради множеството излишни изчис­ле­ния (на едни и същи членове на редицата) в следствие на рекур­сив­ните извиквания.

На предимствата и недостатъците от използване на рекурсия, ще се спрем в детайли малко по-късно в настоящата тема.

Пряка и косвена рекурсия

Когато в тялото на метод се извършва извикване на същия метод, казваме, че методът е пряко рекурсивен.

Ако метод A се обръща към метод B, B към C, а С отново към А, казваме, че методът А, както и методите В и C са непряко (косвено) рекур­сивни или взаимно-рекурсивни.

Веригата от извиквания при косвената рекурсия може да съдържа множество методи, както и разклонения, т.е. при наличие на едно условие да се извиква един метод, а при различно условие да се извиква друг.

Дъно на рекурсията

Реализирайки рекурсия, трябва да сме сигурни, че след краен брой стъпки ще получим конкретен резултат. Затова трябва да имаме един или няколко случаи, чието решение можем да намерим директно, без рекур­сивно извикване. Тези случаи наричаме дъно на рекурсията.

В примера с числата на Фибоначи, дъното на рекурсията е случаят, когато n e по-малко или равно на 2. При него можем директно да върнем резул­тат, без да извършваме рекурсивни извиквания, тъй като по дефиниция първите два члена на редицата на Фибоначи са равни на 1.

Ако даден рекурсивен метод няма дъно на рекурсията, тя ще стане безкрайна и резултатът ще е StackOverflowException.

Създаване на рекурсивни методи

Когато създаваме рекурсивни методи, трябва разбием задачата, която решаваме, на подзадачи, за чието решение можем да използваме същия алгоритъм (рекурсивно).

Комбинирането на решенията на всички подзадачи, трябва да води до решение на изходната задача.

При всяко рекурсивно извикване, проблемната област трябва да се огра­ничава така, че в даден момент да бъде достигнато дъното на рекурсията, т.е. разбиването на всяка от подзадачите трябва да води рано или късно до дъното на рекурсията.

Рекурсивно изчисляване на факториел

Използването на рекурсия ще илюстрираме с един класически пример – рекурсивно изчисляване на факториел.

Факториел от n (записва се n!) е произведението на естествените числа от 1 до n, като по дефиниция 0! = 1.

n! = 1.2.3…n

Рекурентна дефиниция

При създаването на нашето решение, много по-удобно е да използваме съответната рекурентна дефиниция на факториел:

n! = 1, при n = 0

n! = n.(n-1)! за n>0

Намиране на рекурентна зависимост

Наличието на рекурентна зависимост не винаги е очевидно. Понякога се налага сами да я открием. В нашия случай можем да направим това, анализирайки проблема и пресмятайки стойностите на факториел за първите няколко естествени числа.

0! = 1 1! = 1 = 1.1 = 1.0! 2! = 2.1 = 2.1! 3! = 3.2.1 = 3.2! 4! = 4.3.2.1 = 4.3! 5! = 5.4.3.2.1 = 5.4!

От тук лесно се вижда рекурентната зависимост:

n! = n.(n-1)!

Реализация на алгоритъма

Дъното на нашата рекурсия е най-простият случай n = 0, при който стойността на факториел е 1.

В останалите случаи, решаваме задачата за n-1 и умножаваме получения резултат по n. Така след краен брой стъпки, със сигурност ще достигнем дъното на рекурсията, понеже между 0 и n има краен брой естествени числа.

След като имаме налице тези ключови условия, можем да реализираме метод изчисляващ факториел:

static decimal Factorial(int n) {       // The bottom of the recursion       if (n == 0)       {             return 1;       }       // Recursive call: the method calls itself       else       {             return n * Factorial(n - 1);       } }

Използвайки този метод, можем да създадем приложение, което чете от конзолата цяло число, изчислява факториела му и отпечатва получената стойност:

RecursiveFactorial.cs

using System;   class RecursiveFactorial {       static void Main()       {             Console.Write("n = ");             int n = int.Parse(Console.ReadLine());               decimal factorial = Factorial(n);             Console.WriteLine("{0}! = {1}", n, factorial);       }         static decimal Factorial(int n)       {             // The bottom of the recursion             if (n == 0)             {                   return 1;             }             // Recursive call: the method calls itself             else             {                   return n * Factorial(n - 1);             }       } }

Ето какъв ще бъде резултатът от изпълнението на приложението, ако въведем 5 за стойност на n:

n = 5 5! = 120

Рекурсия или итерация

Изчислението на факториел често се дава като пример при обяснението на понятието рекурсия, но в този случай, както и в редица други, рекур­сията далеч не е най-добрият подход.

Често, ако е зададена рекурентна дефиниция на проблема, рекурентното реше­ние е интуитивно и не представлява трудност, докато итеративно (последователно) решение не винаги е очевидно.

В конкретния случай, реализацията на итеративно решение е също толкова кратка и проста, но малко по-ефективна:

static decimal Factorial(int n) {       decimal result = 1;         for (int i = 1; i <= n; i++)       {             result = result * i;       }         return result; }

Предимствата и недостатъците при използването на рекурсия и итерация ще разгледаме малко по-нататък в настоящата тема.

За момента трябва да запомним, че преди да пристъпим към реализацията на рекурсивно решение, трябва да помислим и за итеративен вариант, след което да изберем по-доброто решение според конкретната ситуация.

Нека се спрем на още един пример, където можем да използваме рекурсия за решаване на проблема, като ще разгледаме и итеративно решение.

Имитация на N вложени цикъла

Често се налага да пишем вложени цикли. Когато те са два, три или друг предварително известен брой, това става лесно. Ако броят им, обаче, не е предварително известен, се налага да търсим алтернативен подход. Такъв е случаят в следващата задача.

Да се напише програма, която симулира изпълнението на N вложени цикъ­ла от 1 до K, където N и K се въвеждат от потребителя. Резултатът от из­пъл­нението на програмата, трябва да е еквивалентен на изпълнението на следния фрагмент:

for (a1 = 1; a1 <= K; a1++)       for (a2 = 1; a2 <= K; a2++)             for (a3 = 1; a3 <= K; a3++)                   ...                   for (aN = 1; aN <= K; aN++)                         Console.WriteLine("{0} {1} {2} ... {N}",                               a1, a2, a3, ..., aN);

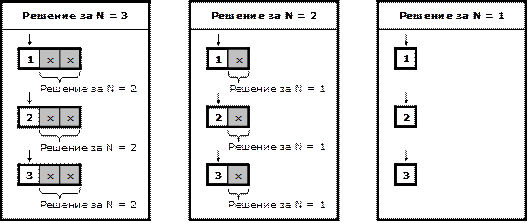
Например при N = 2 и K = 3 (което е еквивалентно на 2 вложени цикъла от 1 до 3) и при N = 3 и K = 3, резултатите трябва да са съответно:

1     1                               1     1     1                       1     2                               1     1     2                       1     3                               1     1     3     N = 2             2     1           N = 3               1     2     1     K = 3 ->          2     2           K = 3 ->                 ...                       2     3                               3     2     3                       3     1                               3     3     1                       3     2                               3     3     2                       3     3                               3     3     3

Алгоритъмът за решаване на тази задача не е така очевиден, както в предходния пример. Нека разгледаме две различни решения – едното рекурсивно, а другото – итеративно.

Всеки ред от резултата, можем да разглеждаме като наредена последова­тел­ност от N числа. Първото число представлява текущата стойност на брояча на първия цикъл, второто на втория и т.н. На всяка една позиция, можем да имаме стойност между 1 и K. Решението на нашата задача се свежда до намирането на всички наредени N-торки за дадени N и K.

Вложени цикли – рекурсивен вариант

Първият проблем, който се изправя пред нас, ако търсим рекурсивен подход за решаване на тази задача, е намирането на рекурентна зависи­мост. Нека се вгледаме малко по-внимателно в при­мера от условието на задачата и да направим някои разсъждения.

Забелязваме, че ако сме пресметнали решението за N = 2, то решението за N = 3 можем да получим, като поставим на първа позиция всяка една от стойностите на К (в случая от 1 до 3), а на останалите 2 позиции поставяме последователно всяка от двойките числа, получени от реше­нието за N = 2. Можем да проверим, че това правило важи и при стойности на N по-големи от 3.

Така получаваме следната зависимост – започвайки от първа позиция, поставяме на текущата позиция всяка една от стойностите от 1 до К и продължаваме рекурсивно със следващата позиция. Това продължава, до­като достигнем позиция N, след което отпечатваме получения резул­тат. Ето как изглежда и съответният метод на C#:

static void NestedLoops(int currentLoop) {       if (currentLoop == numberOfLoops)       {             PrintLoops();             return;       }         for (int counter=1; counter<=numberOfIterations; counter++)       {             loops[currentLoop] = counter;             NestedLoops(currentLoop + 1);       } }

Последователността от стойности ще пазим в масив наречен loops, който при нужда ще бъде отпечатван от метода PrintLoops().

Методът NestedLoops(…) има един параметър, указващ текущата пози­ция, на която ще поставяме стойности.

В цикъла, поставяме после­до­ва­тел­но на текущата позиция всяка една от възможните стойности (про­мен­ли­вата numberOfIterations съдържа стой­ността на К въведена от потребителя), след което извикваме рекурсивно метода NestedLoops(…) за следващата позиция.

Дъното на рекурсията се достига, когато текущата позиция достигне N (променливата numberOfLoops съдържа стойността на N въведена от пот­ребителя). В този момент имаме стойности на всички позиции и отпе­чат­ваме последователността.

Ето и цялостна реализация на решението:

RecursiveNestedLoops.cs

using System;   class RecursiveNestedLoops {       static int numberOfLoops;       static int numberOfIterations;       static int[] loops;         static void Main()       {             Console.Write("N = ");             numberOfLoops = int.Parse(Console.ReadLine());               Console.Write("K = ");             numberOfIterations = int.Parse(Console.ReadLine());               loops = new int[numberOfLoops];               NestedLoops(0);       }         static void NestedLoops(int currentLoop)       {             if (currentLoop == numberOfLoops)             {                   PrintLoops();                   return;             }               for (int counter=1; counter<=numberOfIterations; counter++)             {                   loops[currentLoop] = counter;                   NestedLoops(currentLoop + 1);             }       }         static void PrintLoops()       {             for (int i = 0; i < numberOfLoops; i++)             {                   Console.Write("{0} ", loops[i]);             }             Console.WriteLine();       } }

Ако стартираме приложението и въведем за стойности на N и К съответно 2 и 4, ще получим следния резултат:

N = 2 K = 4 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 3 1 3 2 3 3 3 4 4 1 4 2 4 3 4 4

В метода Main() въвеждаме стойности за N и К, създаваме масива, в който ще пазим последователността от стойности, след което извикваме метода NestedLoops(…), започвайки от първа позиция.

Забележете, че като параметър на метода подаваме 0, понеже пазим после­дователността от стойности в масив, а както вече знаем, номе­ра­ци­ята на елементите в масив започва от 0.

Методът PrintLoops() обхожда всички елементи на масива и ги от­пе­чат­ва на конзолата.

Вложени цикли – итеративен вариант

За реализацията на итеративно решение, можем да използваме следния алгоритъм, който на всяка итерация намира следващата последователност от числа и я отпечатва:

1.  В начално състояние на всички позиции поставяме числото 1.

2.  Отпечатваме текущата последователност от числа.

3.  Увеличаваме с единица числото намиращо се на позиция N. Ако получената стойност е по-голяма от К, заменяме я с 1 и увели­ча­ва­ме с единица стойността на позиция N-1. Ако и нейната стойност е станала по-голяма от К, също я заменяме с 1 и увеличаваме с единица стойността на позиция N-2 и т.н.

4.  Ако стойността на първа позиция, е станала по-голяма от К, алгоритъмът приключва работа.

5.  Преминаваме към стъпка 2.

Следва примерна реализация на описания алгоритъм:

IterativeNestedLoops.cs

using System;   class IterativeNestedLoops {       static int numberOfLoops;       static int numberOfIterations;       static int[] loops;         static void Main()       {             Console.Write("N = ");             numberOfLoops = int.Parse(Console.ReadLine());               Console.Write("K = ");             numberOfIterations = int.Parse(Console.ReadLine());               loops = new int[numberOfLoops];               NestedLoops();       }         static void NestedLoops()       {             InitLoops();               int currentPosition;               while (true)             {                   PrintLoops();                     currentPosition = numberOfLoops - 1;                   loops[currentPosition] = loops[currentPosition] + 1;                     while (loops[currentPosition] > numberOfIterations)                   {                         loops[currentPosition] = 1;                         currentPosition--;                           if (currentPosition < 0)                         {                               return;                         }                         loops[currentPosition] = loops[currentPosition] + 1;                   }             }       }         static void InitLoops()       {             for (int i = 0; i < numberOfLoops; i++)             {                   loops[i] = 1;             }       }         static void PrintLoops()       {             for (int i = 0; i < numberOfLoops; i++)             {                   Console.Write("{0} ", loops[i]);             }             Console.WriteLine();       } }

Методите Main() и PrintLoops() са същите, както в реализацията на рекурсивното решение.

Различен е методът NestedLoops(), който сега реализира алгоритъма за итеративно решаване на проблема и поради това не приема параметър, както в рекурсивния вариант.

В самото начало на този метод извикваме метода InitLoops(), който об­хож­да елементите на масива и поставя на всички позиции единици.

Стъпките на алгоритъма реализираме в безкраен цикъл, от който ще изле­зем в подходящ момент, прекратявайки изпълнението на метода чрез опе­ра­тора return.

Интересен е начинът, по който реализираме стъпка 3 от алгоритъма. Про­вер­ката за стойности по-големи от К, заменянето им с единица и увели­ча­ва­не­то на стойността на предходна позиция (след което правим същата проверка и за нея), реализираме с помощта на един while цикъл, в който влизаме само, ако стойността е по-голяма от К.

За целта първо заменяме стойността на текущата позиция с единица. След това текуща става позицията преди нея. После увеличаваме стойността на новата позиция с единица и се връщаме в началото на цикъла. Тези действия продължават, докато стойността на текуща позиция не се окаже по-малка или равна на К (про­мен­ли­вата numberOfIterations съдържа стойността на К), при което излизаме от цикъла.

В момента, когато на първа позиция стойността стане по-голяма от К (това е моментът, когато трябва да приключим изпълнението), на нейно място поставяме единица и опитваме да увеличим стойността на предходната позиция. В този момент стойността на променливата currentPosition става отрицателна (понеже първата позиция в масив е 0), при което прекра­тяваме изпълнението на метода чрез оператора return. С това за­да­чата ни е изпълнена.

Можем да тестваме, примерно с N=3 и K=2:

N = 3 K = 2 1 1 1 1 1 2 1 2 1 1 2 2 2 1 1 2 1 2 2 2 1 2 2 2

Кога да използваме рекурсия и кога итерация?

Когато алгоритъмът за решаване на даден проблем е рекурсивен, реали­зи­рането на рекурсивно решение, може да бъде много по-четливо и еле­гантно от реализирането на итеративно решение на същия проблем.

Понякога дефинирането на еквивалентен итеративен алгоритъм е зна­чи­тел­но по-трудно и не е лесно да се докаже, че двата алгоритъма са екви­ва­лентни.

В определени случаи, чрез използването на рекурсия, можем да постиг­нем много по-прости, кратки и лесни за разбиране решения.

От друга страна, рекурсивните извиквания, може да консумират много повече ресурси и памет. При всяко рекурсивно извикване, в стека се заделя нова памет за аргументите, локалните променливи и връщаните резултати. При прекалено много рекурсивни извиквания може да се по­лу­чи препълване на стека, поради недостиг на памет.

В дадени ситуации рекурсивните решения може да са много по-трудни за раз­би­ра­не и проследяване от съответните итеративни решения.

Рекурсията е мощна програмна техника, но трябва внимателно да пре­це­ня­ваме, преди да я използваме. При неправилна употреба, тя може да до­ве­де до неефективни и трудни за разбиране и поддръжка решения.

Ако чрез използването на рекурсия, постигаме по-просто, кратко и по-лесно за разбиране решение, като това не е за сметка на ефективността и не предизвиква други странични ефекти, тогава можем да предпочетем рекурсивното решение. В противен случай, е добре да помислим дали не е по-подходящо да използваме итерация.

Числа на Фибоначи – неефективна рекурсия

Нека се върнем отново към примера с намирането на n-тото число на Фибоначи и да разгледаме по-подробно рекурсивното решение:

static long Fib(int n) {       if (n <= 2)       {             return 1;       }       return Fib(n - 1) + Fib(n - 2); }

Това решение е интуитивно, кратко и лесно за разбиране. На пръв поглед изглежда, че това е чудесен пример за приложение на рекурсията. Исти­ната е, че това е един от класическите примери за неподходящо из­пол­зване на рекурсия. Нека стартираме следното приложение:

RecursiveFibonacci.cs

using System;   class RecursiveFibonacci {       static void Main()       {             Console.Write("n = ");             int n = int.Parse(Console.ReadLine());               long result = Fib(n);             Console.WriteLine("fib({0}) = {1}", n, result);       }         static long Fib(int n)       {             if (n <= 2)             {                   return 1;             }             return Fib(n - 1) + Fib(n - 2);       } }

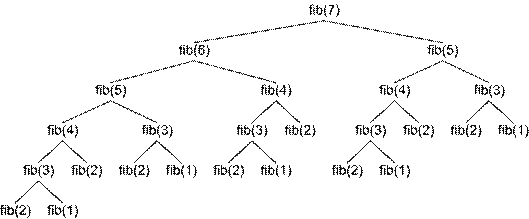
Ако зададем като стойност n = 100, изчисленията ще отнемат толкова дълго време, че едва ли някой ще изчака, за да види резултата. Причи­ната за това е, че подобна реализация е изключително неефектив­на. Всяко рекурсивно извикване води след себе си още две, при което дървото на извикванията расте експоненциално, както е показано на фигурата по-долу.

Броят на стъпките за изчисление на fib(100) е от порядъка на 1.6 на степен 100 (това се доказва математически), докато при линейно решение е само 100.

Проблемът произлиза от това, че се правят напълно излишни изчисления. Повечето членове на редицата се пресмятат многократно. Може да обър­нете внимание колко много пъти на фигурата се среща fib(2).

Числа на Фибоначи – ефективна рекурсия

Можем да оптимизираме рекурсивния метод за изчисление на числата на Фибоначи, като записваме вече пресметнатите числа в масив и извърш­ваме рекурсивно извикване само ако числото, което пресмятаме, не е било вече пресметнато до момента. Благодарение на тази малка оптими­зационна техника (известна в компютърните науки и в динамичното оптимиране с термина memoization), рекур­сивното реше­ние ще работи за линеен брой стъпки. Ето при­ме­рна реализация:

RecursiveFibonacciMemoization.cs

using System;   class RecursiveFibonacciMemoization {       static long[] numbers;         static void Main()       {             Console.Write("n = ");             int n = int.Parse(Console.ReadLine());               numbers = new long[n + 2];             numbers[1] = 1;             numbers[2] = 1;               long result = Fib(n);             Console.WriteLine("fib({0}) = {1}", n, result);       }         static long Fib(int n)       {             if (0 == numbers[n])             {                   numbers[n] = Fib(n - 1) + Fib(n - 2);             }               return numbers[n];       } }

Забелязвате ли разликата? Докато при първоначалния вариант, при n = 100, ни се струва, че изчисле­ни­ята продължават безкрайно дълго, а при оптимизираното решение, полу­ча­ваме отговор мигновено:

n = 100 fib(100) = 3736710778780434371

Числа на Фибоначи – итеративно решение

Не е трудно да забележим, че можем да решим проблема и без изпол­зва­не­то на рекурсия, пресмятайки числата на Фибоначи последователно. За целта ще пазим само последните два пресметнати члена на редицата и чрез тях ще получаваме следващия. Следва реализация на итеративния алгоритъм:

IterativeFibonacci.cs

using System;   class IterativeFibonacci {       static void Main()       {             Console.Write("n = ");             int n = int.Parse(Console.ReadLine());               long result = Fib(n);             Console.WriteLine("fib({0}) = {1}", n, result);       }         static long Fib(int n)       {             long fn = 1;             long fnMinus1 = 1;             long fnMinus2 = 1;               for (int i = 2; i < n; i++)             {                   fn = fnMinus1 + fnMinus2;                     fnMinus2 = fnMinus1;                   fnMinus1 = fn;             }               return fn;       } }

Това решение е също толкова кратко и елегантно, но не крие рисковете от използването на рекурсия. Освен това то е ефективно и не изисква допъл­ни­телна памет.

Изхождайки от горните примери, можем да дадем следната препоръка:

Избягвайте рекурсията, освен, ако не сте сигурни как работи тя и какво точно се случва зад кулисите. Рекур­сията е голямо и мощно оръжие, с което лесно можете да се застреляте в крака. Ползвайте я внимателно!

Ако следваме това правило, ще намалим значително вероятността за не­пра­вилно използване на рекурсия и последствията, произтичащи от него.

Още за рекурсията и итерацията

По принцип, когато имаме линеен изчислителен процес, не трябва да използваме рекурсия, защото итерацията може да се реализира изключи­телно лесно и води до прости и ефективни изчисления. Пример за линеен изчислителен процес е изчислението на факториел. При него изчисляваме членовете на редица, в която всеки следващ член зависи единствено от предходните.

Линейните изчислителни процеси се характеризират с това, че на всяка стъпка от изчисленията рекурсията се извиква еднократно, само в една посока. Схематично линейният изчислителен процес можем да опишем така:

void Recursion(parameters) {       do some calculations;       Recursion(some parameters);       do some calculations; }

При такъв процес, когато имаме само едно рекурсивно извикване в тялото на рекурсивния метод, не е нужно да ползваме рекурсия, защото итера­цията е очевидна.

Понякога, обаче имаме разклонен или дървовиден изчислителен процес. Например имитацията на N вложени цикъла не може лесно да се замени с итерация. Вероятно сте забелязали, че нашият итеративен алго­ритъм, който имитира вложените цикли, работи на абсолютно разли­чен принцип. Опитайте да реализирате същото поведение без рекурсия и ще се убедите, че не е лесно.

По принцип всяка рекурсия може да се сведе до итерация чрез използ­ване на стек на извикванията (какъвто се създава по време на изпъл­нение на програмата), но това е сложно и от него няма никаква полза. Рекурсията трябва да се ползва, когато дава просто, лесно за разбиране и ефективно решение на даден проблем, за който няма очевидно итера­тивно решение.

При дървовидните изчислителни процеси на всяка стъпка от рекурсията, се извършват няколко на брой рекур­сивни извиквания и схемата на извършване на изчисленията може да се визуализира като дърво (а не като списък, както при линейните изчисления). Например при изчисле­нието на числата на Фибоначи видяхме какво дърво на рекурсивните извиквания се получава.

Типичната схема на дървовидния изчислителен процес можем да опишем чрез псевдокод така:

void Recursion(parameters) {       do some calculations;       Recursion(some parameters);       ...       Recursion(some other parameters);       do some calculations; }

Дървовидните изчислителни процеси не могат директно да бъдат сведени до рекурсивни (за разлика от линейните). Случаят с числата на Фибоначи е простичък, защото всяко следващо число се изчислява чрез предход­ните, които можем да изчислим предварително. Понякога, обаче всяко следващо число се изчислява не само чрез предходните, а и чрез следва­щите и рекурсивната зависимост не е толкова проста. В такъв случай рекурсията се оказва особено ефективна.

Ще илюстрираме последното твърдение с един класически пример.

Търсене на пътища в лабиринт – пример

Даден е лабиринт, който има правоъгълна форма и се състои от N*M квадратчета. Всяко квадратче е или проходимо, или не е проходимо. Търсач на приключения влиза в лабиринта от горния му ляв ъгъл (там е входът) и трябва да стигне до долния десен ъгъл на лабиринта (там е изходът). Търсачът на приключения може на всеки ход да се премести с една позиция нагоре, надолу, наляво или надясно, като няма право да излиза извън границите на от лабиринта и няма право да стъпва върху непроходими квадратчета. Преминаването през една и съща позиция повече от веднъж също е забранено (счита се, че търсачът на приклю­чения се е загубил, ако се върне след няколко хода на място, където вече е бил). Да се напише компютърна програма, която отпечатва всички възможни пътища от началото до края на лабиринта.

Това е типичен пример за задача, която може лесно да се реши с рекурсия, докато с итерация решението е по-сложно и по-трудно за реализация.

Нека първо си нарисуваме един пример, за да си представим условието на задачата и да помислим за решение:

Видно е, че има 3 различни пътя от началната позиция до крайната, които отговарят на изискванията на задачата (движение само по празни квадратчета и без преминаване по два пъти през никое от тях). Ето как изглеждат въпросните 3 пътя:

s 1 2             3         6 5 4         7             8 9 10 11 12 13 14

s 1 2   8 9 10     3   7   11     4 5 6   12             13             14

s 1 2             3             4 5 6 7 8             9             10

На фигурата по-горе с числата от 1 до 14 е означен номерът на съответната стъпка от пътя.

Пътища в лабиринт – рекурсивен алгоритъм

Как да решим задачата? Можем да разгледаме търсенето на дадена позиция в лабиринта до края на лабиринта като рекурсивен процес по следния начин:

-     Нека текущата позиция в лабиринта е (row, col). В началото тръг­ваме от стартовата позиция (0,0).

-     Ако текущата позиция e търсената позиция (N-1, M-1), то сме намерили път и трябва да го отпечатаме.

-     Ако текущата позиция е непроходима, връщаме се назад (нямаме право да стъпваме в нея).

-     Ако текущата позиция е вече посетена, връщаме се назад (нямаме право да стъпваме втори път в нея).

-     В противен случай търсим път в четирите възможни посоки. Търсим рекурсивно (със същия алгоритъм) път към изхода на лабиринта като опитваме да ходим във всички възможни посоки:

o   Опитваме наляво: позиция (row, col-1).

o   Опитваме нагоре: позиция (row-1, col).

o   Опитваме надясно: позиция (row, col+1).

o   Опитваме надолу: позиция (row+1, col).

За да стигнем до този алгоритъм, разсъждаваме рекурсивно. Имаме задачата "търсене на път от дадена позиция до изхода". Тя може да се сведе до 4 подзадачи:

-     търсене на път от позицията вляво от текущата до изхода;

-     търсене на път от позицията нагоре от текущата до изхода;

-     търсене на път от позицията вдясно от текущата до изхода;

-     търсене на път от позицията надолу от текущата до изхода.

Ако от всяка възможна позиция, до която достигнем, проверим четирите възможни посоки и не се въртим в кръг (избягваме преминаване през позиция, на която вече сме били), би трябвало рано или късно да намерим изхода (ако съществува път към него).

Този път рекурсията не е толкова проста, както при предните задачи. На всяка стъпка трябва да проверим дали не сме стигнали изхода и дали не стъпваме в забранена позиция, след това трябва да отбележим позицията като посетена и да извикаме рекурсивното търсене на път в четирите посоки. След връщане от рекурсивните извиквания, трябва да отбележим обратно като непосетена позицията, от която се оттегляме. Такова обхождане е известно в информатиката като търсене с връщане назад (backtracking).

Пътища в лабиринт – имплементация

За реализацията на алгоритъма ще ни е необходимо представяне на лабиринта. Ще ползваме двумерен масив от символи, като в него ще означим със символа ' ' (интервал) проходимите позиции, с 'e' изхода от лабиринта и с '*' непроходимите полета. Стартовата позиция ще означим като празна. Позициите, през които сме минали, ще означим със символа 's'. Ето как ще изглежда дефиницията на лабиринта за нашия пример:

static char[,] lab = {       {' ', ' ', ' ', '*', ' ', ' ', ' '},       {'*', '*', ' ', '*', ' ', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', ' '},       {' ', '*', '*', '*', '*', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', 'е'}, };

Нека се опитаме да реализираме рекурсивния метод за търсене в лабиринт. Той трябва да бъде нещо такова:

static char[,] lab = {       {' ', ' ', ' ', '*', ' ', ' ', ' '},       {'*', '*', ' ', '*', ' ', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', ' '},       {' ', '*', '*', '*', '*', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', 'е'}, };   static void FindPath(int row, int col) {       if ((col < 0) || (row < 0) ||             (col >= lab.GetLength(1)) || (row >= lab.GetLength(0)))       {             // We are out of the labyrinth             return;       }         // Check if we have found the exit       if (lab[row, col] == 'е')       {             Console.WriteLine("Found the exit!");       }         if (lab[row, col] != ' ')       {             // The current cell is not free             return;       }         // Mark the current cell as visited       lab[row, col] = 's';         // Invoke recursion to explore all possible directions       FindPath(row, col - 1); // left       FindPath(row - 1, col); // up       FindPath(row, col + 1); // right       FindPath(row + 1, col); // down         // Mark back the current cell as free       lab[row, col] = ' '; }   static void Main() {       FindPath(0, 0); }

Имплементацията стриктно следва описанието, дадено по-горе. В случая размерът на лабиринта не е записан в променливи N и M, а се извлича от двумерния масив lab, съхраняващ лабиринта: броят колони е lab. GetLength(1), а броят редове е lab.GetLength(0).

При влизане в рекурсивния метод за търсене първо се проверява дали няма излизане извън лабиринта. Ако има, търсенето от текущата позиция нататък се прекратява, защото е забранено излизане извън границите на лабиринта.

След това се проверява дали не сме намерили изхода. Ако сме го намерили, се отпечатва подходящо съобщение и търсенето от текущата позиция нататък приключва.

След това се проверява дали е свободна текущата клетка. Клетката е свободна, ако е проходима и не сме били на нея при някоя от предните стъпки (ако не е част от текущия път от стартовата позиция до текущата клетка на лабиринта).

При свободна клетка, се осъществява стъпване в нея. Това се извършва като се означи клет­ката като заета (със символа 's'). След това рекур­сивно се търси път в четирите възможни посоки. След връщане от рекур­сивното проучване на четирите възможни посоки, се отстъпва назад от текущата клетка и тя се маркира отново като свободна (връщане назад).

Маркирането на текущата клетка като свободна при излизане от рекурси­ята е важно, защото при връщане назад тя вече не е част от текущия път. Ако бъде пропуснато това действие, няма да бъдат намерени всички пътища до изхода, а само някои от тях.

Така изглежда рекурсивният метод за търсене на изхода в лабиринта. Остава само да го извикаме от Main() метода, започвайки търсенето на пътя от началната позиция (0, 0).

Ако стартираме програмата, ще видим следния резултат:

Found the exit! Found the exit! Found the exit!

Вижда се, че изходът е бил намерен точно 3 пъти. Изглежда алгоритъмът работи коректно. Липсва ни обаче отпечатването на самия път като после­дователност от позиции.

Пътища в лабиринт – запазване на пътищата

За да можем да отпечатаме пътищата, които намираме с нашия рекур­сивен алгоритъм, можем да използваме масив, в който при всяко прид­вижване пазим посоката, която сме поели (L – наляво, U – нагоре, R – надясно, D – надолу). Този масив ще съдържа във всеки един момент текущия път от началото на лабиринта до текущата позиция.

Ще ни трябва един масив от символи и един брояч на стъпките, които сме направили. Броячът ще пази колко пъти сме се придвижили към следваща позиция рекурсивно, т.е. текущата дълбочина на рекурсията.

За да работи всичко коректно, е необходимо преди влизане в рекурсия да увеличаваме брояча и да запазваме посоката, която сме поели в текущата позиция от масива, а при връщане от рекурсията – да намаляваме брояча. При намиране на изхода можем да отпечатаме пътя – всички символи от масива от 0 до позицията, която броячът сочи.

Колко голям да бъде масивът? Отговорът на този въпрос е лесен; понеже в една клетка можем да влезем най-много веднъж, то никога пътят няма да е по-дълъг от общия брой клетки в лабиринта (N*M). В нашия случай размерът е 7*5, т.е. масивът е достатъчно да има 35 позиции.

Следва една примерна имплементация на описаната идея:

static char[,] lab = {       {' ', ' ', ' ', '*', ' ', ' ', ' '},       {'*', '*', ' ', '*', ' ', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', ' '},       {' ', '*', '*', '*', '*', '*', ' '},       {' ', ' ', ' ', ' ', ' ', ' ', 'е'}, };   static char[] path =       new char[lab.GetLength(0) * lab.GetLength(1)]; static int position = 0;   static void FindPath(int row, int col, char direction) {       if ((col < 0) || (row < 0) ||             (col >= lab.GetLength(1)) || (row >= lab.GetLength(0)))       {             // We are out of the labyrinth             return;       }         // Append the direction to the path       path[position] = direction;       position++;         // Check if we have found the exit       if (lab[row, col] == 'е')       {             PrintPath(path, 1, position - 1);       }         if (lab[row, col] == ' ')       {             // The current cell is free. Mark it as visited             lab[row, col] = 's';               // Invoke recursion to explore all possible directions             FindPath(row, col - 1, 'L'); // left             FindPath(row - 1, col, 'U'); // up             FindPath(row, col + 1, 'R'); // right             FindPath(row + 1, col, 'D'); // down               // Mark back the current cell as free             lab[row, col] = ' ';       }         // Remove the direction from the path       position--; }   static void PrintPath(       char[] path, int startPos, int endPos) {       Console.Write("Found path to the exit: ");       for (int pos = startPos; pos <= endPos; pos++)       {             Console.Write(path[pos]);       }       Console.WriteLine(); }   static void Main() {       FindPath(0, 0, 'S'); }

За леснота добавихме още един параметър на рекурсивния метод за търсене на път до изхода от лабиринта: посоката, в която сме поели, за да дойдем на текущата позиция. Този параметър няма смисъл при първо­на­чалното започване от стартовата позиция и затова в началото слагаме за посока някаква безсмислена стойност 'S'. След това при отпечатването пропускаме първия елемент от пътя.

Ако стартираме програмата, ще получим трите възможни пътя от началото до края на лабиринта:

Found path to the exit: RRDDLLDDRRRRRR Found path to the exit: RRDDRRUURRDDDD Found path to the exit: RRDDRRRRDD

Пътища в лабиринт – тестване на програмата

Изглежда алгоритъмът работи. Остава да го тестваме с още малко примери, за да се убедим, че не сме допуснали някоя глупава грешка. Може да пробваме примерно с празен лабиринт с размер 1 на 1, с празен лабиринт с размер 3 на 3 и примерно с лабиринт, в който не съществува път до изхода, и накрая с огромен лабиринт, където пътищата са наистина много.

Ако изпълним тестовете, ще се убедим, че във всеки от тези необичайни случаи програмата работи коректно.

Примерен вход (лабиринт 1 на 1):

static char[,] lab = {       {'е'}, };

Примерен изход:

Found path to the exit:

Вижда се, че изходът е коректен, но пътят е празен (с дължина 0), тъй като стартовата позиция съвпада с изхода. Бихме могли да подобрим визуализацията в този случай (примерно да отпечатваме "Empty path").

Примерен вход (празен лабиринт 3 на 3):

static char[,] lab = {       {' ', ' ', ' '},       {' ', ' ', ' '},       {' ', ' ', 'е'}, };

Примерен изход:

Found path to the exit: RRDLLDRR Found path to the exit: RRDLDR Found path to the exit: RRDD Found path to the exit: RDLDRR Found path to the exit: RDRD Found path to the exit: RDDR Found path to the exit: DRURDD Found path to the exit: DRRD Found path to the exit: DRDR Found path to the exit: DDRUURDD Found path to the exit: DDRURD Found path to the exit: DDRR

Вижда се, че изходът е коректен – това са всички пътища до изхода.

Примерен вход (лабиринт 5 на 3 без път до изхода):

static char[,] lab = {       {' ', '*', '*', ' ', ' '},       {' ', ' ', ' ', '*', ' '},       {'*', ' ', ' ', '*', 'e'}, };

Примерен изход:

(няма изход)

Вижда се, че изходът е коректен, но отново бихме могли да добавим по-приятелско съобщения (примерно "No exit!") вместо липса на какъвто и да е изход.

Сега остана да проверим какво се случва, когато имаме голям лабиринт. Ето примерен вход (лабиринт с размер 15 на 9):

static char[,] lab = {       {' ','*',' ',' ',' ',' ','*',' ',' ',' ',' ','*','*',' ',' '},       {' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ','*','*','*',' ','*',' ',' ',' ',' ',' ','*','*','*','*'},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ','е'}, };

Стартираме програмата и тя започва да печата непрекъснато пътища до изхода, но не свършва, защото пътищата са прекалено много. Ето как изглежда една малка част от изхода:

Found path to the exit: DRDLDRRURUURRDLDRRURURRRDLLDLDRRURRURRURDDLLDLLDLLLDRRDLDRDRRURDRR Found path to the exit: DRDLDRRURUURRDLDRRURURRRDLLDLDRRURRURRURDDLLDLLDLLLDRRDLDRDRRRURRD Found path to the exit: DRDLDRRURUURRDLDRRURURRRDLLDLDRRURRURRURDDLLDLLDLLLDRRDLDRDRRRURDR ...

Сега, нека пробваме един последен пример – лабиринт с голям размер (15 на 9, в който не съществува път до изхода:

static char[,] lab = {       {' ','*',' ',' ',' ',' ','*',' ',' ',' ',' ','*','*',' ',' '},       {' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ',' ',' '},       {' ','*','*','*',' ','*',' ',' ',' ',' ',' ','*','*','*','*'},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ','*','*',' ',' '},       {' ',' ',' ',' ',' ','*',' ',' ',' ',' ',' ',' ',' ','*','е'}, };

Стартираме програмата и тя заспива, без да отпечата нищо. Всъщност работи прекалено дълго, за да я изчакаме. Изглежда имаме проблем.

Какъв е проблемът? Проблемът е, че възможните пътища, които алгори­тъмът анализира, са прекалено много и изследването им отнема прека­лено много време. Да помислим колко се тези пътища. Ако средно един път до изхода е 20 стъпки и ако на всяка стъпка имаме 4 възможни посоки за продъл­жение, то би трябвало да анализираме 4²⁰ възможни пътя, което е ужасно голямо число. Тази оценка на броя възможности е изключително неточна, но дава ориентация за какъв порядък възможности става дума.

Какъв е изводът? Изводът е, че методът "търсене с връщане назад" (backtracking) не работи, когато вариантите са прекалено много, а фактът, че са прекалено много лесно може да се установи.

Няма да ви мъчим с опити да измислите решение на задачата. Проблемът за намиране на всички пътища в лабиринт няма ефективно решение при големи лаби­ринти.

Задачата има ефективно решение, ако бъде формулирана по друг начин: да се намери поне един изход от лабиринта. Тази задача е далеч по-лесна и може да се реши с една много малка промяна в примерния код: при връщане от рекурсията текущата позиция да не се маркира обратно като свободна. Това означава да изтрием следните редове код:

// Mark back the current cell as free lab[row, col] = ' ';

Можем да се убедим, че след тази промяна, програмата много бързо установява, ако в лабиринта няма път до изхода, а ако има – много бързо намира един от пътищата (произволен).

Използване на рекурсия – изводи

Какъв е генералният извод от задачата за търсене на път в лабиринт? Изводът вече го формулирахме: ако не разбирате как работи рекурсията, избягвайте да я ползвате! Внимавайте, когато пишете рекурсивен код. Рекурсията е много мощен метод за решаване на комбинаторни задачи (задачи, в които изчерпваме варианти), но не е за всеки. Можете много лесно да сгрешите. Лесно можете да накарате програмата да "зависне" или да препълните стека с бездънна рекурсия. Винаги търсете итератив­ните решения, освен, ако не разбирате в голяма дълбочина как да ползвате рекурсията!

Колкото до задачата за търсене на най-къс път в лабиринт, можете да я решите елегантно без рекурсия с т.нар. метод на вълната, известен още като BFS (breadth-first search), който се реализира елементарно с една опашка. Повече за алгоритъма "BFS" можете да прочетете на неговата страница в Уикипедия: http://en.wikipedia.org/wiki/Breadth-first_search.

Упражнения

1.      Напишете програма, която симулира изпълнението на n вложени цикъла от 1 до n. Пример:

1 1 1

                                                                                                                   1 1 2

                                                            1 1 3

1 1                                                                                        1 2 1

n=2 ->           1 2                                                     n=3 ->                   ….     

2 1                                                                                        3 2 3

                                                          2 2                                                                                            3 3 1

3 3 2

                                                                        3 3 3

2.      Напишете рекурсивна програма, която генерира и отпечатва всички комбинации с повторение на k елемента над n-елементно множество.

Примерен вход:

n = 3 k = 2

Примерен изход:

(1 1), (1 2), (1 3), (2 2), (2 3), (3 3)

Измислете и реализирайте итеративен алгоритъм за същата задача.

3.      Напишете рекурсивна програма, която генерира всички вариации с повторение на n елемента от k-ти клас.

Примерен вход:

n = 3 к = 2

Примерен изход:

(1 1), (1 2), (1 3), (2 1), (2 2), (2 3), (3 1), (3 2), (3 3)

Измислете и реализирайте итеративен алгоритъм за същата задача.

4.      Нека е дадено множество от символни низове. Да се напише рекур­сивна програма, която генерира всички подмножества съставени от точно k на брой символни низа, избрани измежду елементите на това множество.

Примерен вход:

strings = {'test', 'rock', 'fun'} k = 2

Примерен изход:

(test rock), (test fun), (rock fun)

Измислете и реализирайте итеративен алгоритъм за същата задача.

5.      Напишете рекурсивна програма, която отпечатва всички подмножества на дадено множество от думи.

Примерен вход:

words = {'test', 'rock', 'fun'}

Примерен изход:

(), (test), (rock), (fun), (test rock), (test fun), (rock fun), (test rock fun)

Измислете и реализирайте итеративен алгоритъм за същата задача.

6.      Реализирайте алгоритъма "сортиране чрез сливане" (merge-sort). При него началният масив се разделя на две равни по големина части, които се сортират (рекурсивно чрез merge-sort) и след това двете сортирани части се сливат, за да се получи целият масив в сортиран вид.

7.      Напишете рекурсивна програма, която генерира и отпечатва пермута­циите на числата 1, 2, …, n, за дадено цяло число n.

Примерен вход:

n = 3

Примерен изход:

(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)

8.      Даден е масив с цели числа и число N. Напишете рекурсивна прог­рама, която намира всички подмножества от числа от масива, които имат сума N. Например ако имаме масива {2, 3, 1, -1} и N=4, можем да получим N=4 като сума по следните два начина: 4=2+3-1; 4=3+1.

9.      Даден е масив с цели положителни числа. Напишете програма, която проверява дали в масива съществуват едно или повече числа, чиято сума е N. Можете ли да решите задачата без рекурсия?

10.   Дадена е матрица с проходими и непроходими клетки. Напишете рекурсивна програма, която намира всички пътища между две клетки в матрицата.

11.   Модифицирайте горната програма, за да проверява дали съществува път между две клетки без да се намират всички възможни пътища. Тествайте за матрица 100х100 пълна само с проходими клетки.

12.   Напишете програма, която намира най-дългата поредица от съседни проходими клетки в матрица.

13.   Даден е двумерен масив с проходими и непроходими клетки. Напишете програма, която намира всички площи съставени само от проходими клетки.

14.   Реализирайте алгоритъма BFS (breath-first search) за търсене на най-кратък път в лаби­ринт. Ако се затруднявате, потърсете информация в Интернет.

15.   Напишете рекурсивна програма, която обхожда целия твърд диск C:\ рекурсивно и отпечатва всички папки и файловете в тях.

Решения и упътвания

1.      Направете метод, в който има цикъл и за всяко завъртане на цикъла да се вика същия метод.

2.      И за рекурсивния и за итеративния вариант на задачата използвайте модификация на алгоритмите за генериране на N вложени цикли.

3.      И за рекурсивния и за итеративния вариант на задачата използвайте модификация на алгоритмите за генериране на N вложени цикли.

4.      Нека низовете са N на брой. Използвайте имитация на k вложени цикли (рекурсивна или итеративна). Трябва да генерирате всички множества от k елемента в диапазона [0...N-1]. За всяко такова множество разглеждате числата от него като индекси в масива със символните низове и отпечатвате за всяко число съответния низ. За горния пример множеството {0, 2} означава нулевата и втората дума, т.е. (test, fun).

5.      Можете да използвате предходната задача и да я извикатe N пъти, за да генерирате последователно празното множество (k=0), следвано от всички подмножества с 1 елемент (k=1), всички подмножества с 2 елемента (k=2), всички подмножества с 3 елемента (k=3) и т.н.

Задачата има и много по-хитро решение: завъртате цикъл от 0 до 2^N-1 и преобразувате всяко от тези числа в двоична бройна система. Например за N=3 имате следните двоични представяния на числата 0 до 2^N-1:

000, 001, 010, 011, 100, 101, 110, 111

Сега за всяко двоично представяне взимате тези думи от множеството символни низове, за които имате единица на съответната позиция в двоичното представяне. Примерно за двоичното представяне "101" взимате първия и последния низ (там има единици) и пропускате втория низ (там има нула). Хитро, нали?

6.      Ако се затрудните, потърсете "merge sort" в Интернет. Ще намерите стотици имплементации, включително на C#. Предизвикателството е да не се заделя при всяко рекурсивно извикване нов масив за резултата, защото това е неефективно, а да се ползват само 3 масива в цялата програма: двата масива, които се сливат и трети за резултата от сливането. Ще трябва да реализирате сливане две области от масив в област от друг масив.

7.      Да предположим, че методът Perm(k) пермутира по всички възможни начини елементите от масив p[], стоящи на позиции от 0 до k включително. В масива p първоначално записваме числата от 1 до N. Можем да реали­зираме рекурсивно Perm(k) по следния начин:

1. При k=0 отпечатваме поредната пермутация и излизаме (дъно на рекурсията).
2. За всяка позиция i от 0 до k-1 извършваме следното:

a.  Разменяме p[i] с p[k].

b.  Извикваме рекурсия: Perm(k-1).

c.   Разменяме обратно p[i] с p[k].

1. Извикваме Perm(k-1).

В началото започваме с извикване на Perm(N-1).

8.      Задачата не се различава съществено от задачата за намиране на всички подмножества измежду даден списък със символни низове. Помислете ще работи ли бързо програмата при 500 числа? Обърнете внимание, че трябва да отпечатаме всички подмножества със сума N, които могат да бъдат ужасно много при голямо N и подходящи числа в масива. По тази причина задачата няма ефективно решение.

9.      Ако подходите към проблема по метода на изчерпването на всички възможности, решението няма да работи при повече от 20-30 еле­мента. Затова може да подходите по съвсем различен начин в случай, че числата в масива са само положителни или са ограничени в някакъв диапазон (примерно [-50…50]). Тогава може да се използва следният оптимиза­ционен алгоритъм с динамично оптимиране:

Нека имаме масива с числа p[]. Нека означим с possible(k, sum) дали можем да получим сума sum като използваме само числата p[0], p[1], ..., p[k]. Тогава са в сила следните рекурентни зависимости:

-     possible(0, sum) = true, точно когато p[0] == sum

-     possible(k, sum) = true, точно когато possible[k-1, sum] == true или possible[k-1, sum-p[k]] == true

Горната формула показва, че можем да получим сума sum от елемен­тите на масива на позиции от 0 до k, ако едно от двете е в сила:

-     Елементът p[k] не участва в сумата sum и тя се получава по някакъв начин от останалите елементи (от 0 до k-1);

-     Елементът p[k] участва в сумата sum, а остатъкът sum-p[k] се получава по някакъв начин от останалите елементи (от 0 до k-1).

Реализацията не е сложна, но трябва да внимавате и да не позволя­вате вече сметната стойност от двумерния масив possible[,] да се пресмята повторно. За целта трябва да пазите за всяко възможно k и sum стойността possible[k, sum]. Иначе алгоритъмът няма да работи при повече 20-30 елемента.

Възстановяването на самите числа, които съставят намерената сума, може да се извърши като се тръгне отзад напред от сумата n, получена от първите k числа, като на всяка стъпка се търси как тази сума може да се получи чрез първите k-1 числа (чрез взимане на k-тото число или пропускането му).

Имайте предвид, че в общия случай всички възможни суми на числа от входния масив може да са ужасно много. Примерно всички възможни суми от 50 int числа в интервала [Int32.MinValue … Int32.MaxValue] са достатъчно много, че да не могат да се съберат в каквато и да е структура от данни. Ако обаче всички числа във входния масив са положителни (както е в нашата задача), може да пазите само сумите в интервала [1..N], защото от останалите са безперспективни и от тях не може да се получи търсената сума N чрез добавяне на едно или повече числа от входния масив.

Ако числата във входния масив не са задължително положителни, но са ограничени в някакъв интервал, тогава и всички възможни суми са ограничени в някакъв интервал и можем да ползваме описания по-горе алгоритъм. Например, ако диапазонът на числата във входния масив е от -50 до 50, то най-малката възможна сума е -50*N, а най-голямата е 50*N.

Ако числата във входния масив са произволни и не са ограничени в някакъв интервал, задачата няма ефективно решение.

Можете да прочетете повече за тази класическа оптимизационна задача в Уикипедия: http://en.wikipedia.org/wiki/Subset_sum_problem.

10.   Прочетете за All Depth-First Search в интернет.

11.   Потърсете в интернет за Depth-First Search или Breath-First Search.

12.   Потърсете в интернет за Depth-First Search или Breath-First Search.

13.   Помислете за подходяща реализация на алгоритъма за търсене в широчина (BFS). След като намерите площ, която отговаря на условията, направете всички нейни клетки непроходими, намерете следващата проходима клетка и потърсете от нея с BFS следващата площ от съседни проходими клетки.

14.   Прочетете статията в Уикипедия: http://en.wikipedia.org/wiki/Breadth-first_search. Там има достатъчно обяснения за BFS и примерен код. За да реализирате опашка в C# използвайте обикновен масив или класа System.Collections.Generics.Queue<T>. За елементи в опашката използвайте собствена структура Point съдържаща x и y координати или кодирайте координатите в число или пък използвайте две опашки – по една за всяка от координатите.

15.   За всяка папка (започвайки от C:\) принтирайте името и файловете на текущата директория и викайте рекурсивно своя метод за всяка поддиректория на текущата.

Демонстрации (сорс код)

Изтеглете демонстрационните примери към настоящата глава от книгата: Рекурсия-Демонстрации.zip.

Дискусионен форум

Коментирайте книгата и задачите в нея във: форума на софтуерната академия.